Inverse Trigonometry-Explanation and Examples

Inverse trigonometric functions use trigonometric ratios to find angles.

There are two ways to write trigonometric functions. The first is to write $fun^-1x$, and the other is $arcfunx$, where $fun$ can be any of the six trigonometric functions.

Just like standard trigonometric functions, inverse trigonometric functions are important in geometry and most branches of science and engineering.

Before moving on with this section, make sure to review the six basic trigonometric functions.

What Are Inverse Trig Functions?

Inverse trigonometry functions are the functions that use trigonometric ratios to find an angle. That is, inverse trigonometry includes functions that are the inverse of sine, cosine, tangent, cosecant, secant, and cotangent.

These functions are arcsine, arccosine, arctangent, arccosecant, arcsecant, and arccotangent. Sometimes, they are also written as $sin^{-1}$, $cos^{-1}$, $tan^{-1}$, $csc^{-1}$, $sec^{-1}$, and $cot^{-1}$. This can be confusing, however, as $x^{-1} = \frac{1}{x}$, but $sin^{-1} \neq \frac{1}{sin}$. That function is actually cosecant.

Since trigonometric functions are periodic, there are infinitely many angles that can produce a given ratio. Typically, however, the inverse functions produce the smallest standard angle that gives such a ratio.

For example, arcsine of $\frac{1}{2}$ is $\frac{\pi}{6}$, even though sine of $\frac{5\pi}{6}$ is also $\frac{1}{2}$.

Sometimes, problems involving inverse trigonometric ratios include the quadrant to distinguish between standard angles with equivalent ratios.

How To Use Inverse Trigonometric Functions

People use inverse trigonometric functions to find an angle when given a ratio, which is especially useful in physical applications. 

For example, a scientist may try to find the angle of incline for a ramp. As long as he knows the length of the ramp and the height, then he can use arcsine or arccosecant to find the unknown angle. In such a case, the triangle is a normal right triangle, so the angle will be in the first quadrant.

Examples

This section covers common examples of problems involving inverse trigonometry and their step-by-step solutions.

Example 1

For which angles on the unit circle is the tangent equal to $1$?

Solution

Typically, people only memorize the sine and cosine of the major angles on a unit circle, but doing this actually gives one enough information to solve this problem. 

If tangent is equal to $1$, then sine and cosine have the same value. But these two functions are only equal at two places on the unit circle. The first is at the angle $\frac{\pi}{4}$. They are equal here because $\frac{\pi}{4}$ is the middle angle in the first quadrant. 

Using the left hand trick, one would bend the middle finger. There are two fingers above, so cosine is equal to $\frac{\sqrt{2}}{2}$. There are also two fingers below, so sine is also equal to $\frac{\sqrt{2}}{2}$. Therefore, the tangent must be equal to $1$ at this angle.

The other angle that will make sine and cosine equal will also be a major angle with a denominator of $4$ since sine and cosine will both have an absolute of $\frac{\sqrt{2}}{2}$.

Then, use the mnemonic All Students Take Calculus to find the quadrant of the second angle. The T in the third word, Take, stands for tangent, indicating the third quadrant has a positive tangent. Therefore, the second angle is in the third quadrant. 

Using the mnemonic ASAP, the major angle with a denominator of $4$ has a numerator coefficient of pi that is one more than the denominator. This is because the third letter is A for add. Thus, the angle $\frac{5\pi}{4}$ also has a tangent of $1$.

Another way to find the first angle, $\frac{\pi}{4}$, is to plug the arctan of $1$ using a calculator.

Example 2

What are the angle measures in a 3-4-5 right triangle?

Solution

One of the angles will be $90$ degrees or $\frac{\pi}{2}$ radians because a 3-4-5 triangle is a right triangle.

The longest side of this triangle has a length of $5$. This will be the hypotenuse. 

Then, the sine of one of the remaining angles is equal to $\frac{4}{5}$, and the sine of the other is $\frac{3}{5}$.

Therefore, one of the remaining angles is equal to arcsine of $\frac{3}{5}$, and the other will be equal to arcsine of $\frac{4}{5}.

At this point, it helps to plug these values into a calculator. Doing so says that the arcsine of the larger angle is about $0.93$ radians, and the arcsine of the smaller angle is about $0.64$ radians. 

Example 3

The arcsecant of an angle, $x$, is $\frac{9}{8}$. What is the cosine of the angle?

Solution

To solve this problem it helps to think about what arcsecant is. Since the arcsecant of the angle is $\frac{9}{8}$, this means that the secant of the angle is $\frac{9}{8}$.

Then, think about how the secant relates to the cosine. It is equal to the reciprocal of the cosine. Therefore, the reciprocal of the secant is cosine.

That is, the cosine is equal to $\frac{8}{9}$.

Note that in this example, finding the actual angle was unnecessary. 

Example 4

A man wants to know the angle of incline for a staircase. He measures the horizontal length along the base of the staircase as twelve feet and the vertical length as eight feet. What is the angle of incline?

Solution

It helps to draw a picture of this situation.

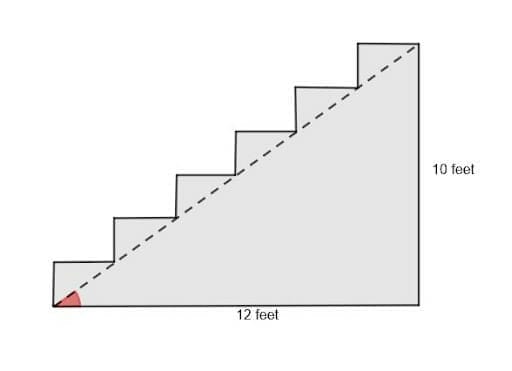
In this case, there is an unknown angle and a known ratio. This is a situation where inverse trigonometric functions, which have ratios as inputs and angles as outputs, help.

Here, the known sides are the ones opposite of and adjacent to the unknown angle. Assume that the stairs are flush to the wall and form a right angle. Then, the known sides give the ratio of tangent, $\frac{o}{a} = \frac{10}{12} = \frac{5}{6}$, or cotangent, $\frac{a}{o} = frac{12}{10} = \frac{6}{5}$. 

Therefore, the unknown angle is equal to arctangent of $\frac{5}{6}$ or arccotangent of $\frac{6}{5}$. Plugging either of these into a calculator gives the angle of $0.69$ radians or $39.8$ degrees.

Example 5

An angle lies in the fourth quadrant and has a sine of $-\frac{2}{3}$. What is the standard angle? Use a calculator to help.

Solution

If an angle has a sine of $-frac{2}{3}$, then the angle is equal to the arcsine of $-\frac{2}{3}$.

Plugging this into a calculator reveals that the angle is about $-0.73$ radians or $-41.8$ radians.

However, negative angles are not standard angles. The equivalent standard angle is $2\pi-0.73$ radians or about $5.55$ radians. In degrees, this is $360-41.8 = 318.2$ degrees.