JUMP TO TOPIC
Locus of a Moving Point – Explanation and Examples
 The locus of a moving point is a path that a given point traces out when it is moving under certain constraints.
The locus of a moving point is a path that a given point traces out when it is moving under certain constraints.
Certain parameters cause the locus to form geometric objects with notable properties.
In this section, we will go over:
- What is a Locus in Geometry?
- Locus Theorems
What is a Locus in Geometry?
Imagine you grabbing a crayon, setting the tip on a piece of paper, and then moving the tip all over the paper. You will trace out a line by doing this, and you will be able to tell quickly where the tip of the crayon has been.
Now, call the paper a plane and the tip a point. Then the locus equivalent in this thought experiment is the colored line traced out by the crayon.
Though the term “locus” (and its plural counterpart, “loci”) is a bit old-fashioned, it essentially refers to a set of points where a point with certain constraints may be found. Using locus terminology is another way of defining certain geometric objects.
In more modern times, mathematicians will more often refer to infinite sets meeting certain criteria than the locus of a moving point meeting certain criteria.
Locus Theorems
There are six well-known locus theorems in geometry. Each describes a constraint for the movement of a point and identifies the locus’s geometric object.
Locus Theorem 1
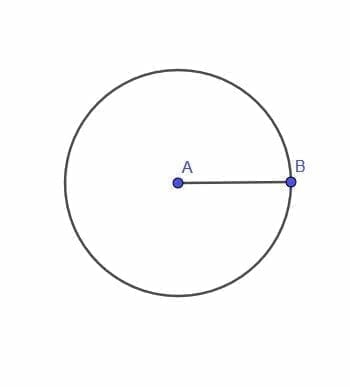
The first locus theorem gives us a point, A, moving with the constraint that it is always a fixed distance $r$ from a point B.
This point will trace out a circle. That is, the locus of such a point is a circle.
By definition, a circle is the set of all points equidistant from another point. Therefore, it makes sense that the locus of A is also a circle.
Locus Theorem 2
The second locus theorem gives us a point, A, that is always a fixed distance, $r$, from a line, $m$.
The locus is the path of A is two lines on either side of $m$, each a distance of $r$ from the original line. These two lines will both be parallel to $m$.
Locus Theorem 3
The third locus theorem gives us a point, A, that is always the same distance from two other points, B and C.
This point will trace out a path that is a line perpendicular to B and C and divides a line segment connecting the two in half. That is, the locus of A is a perpendicular bisector for the line segment BC.
Locus Theorem 4
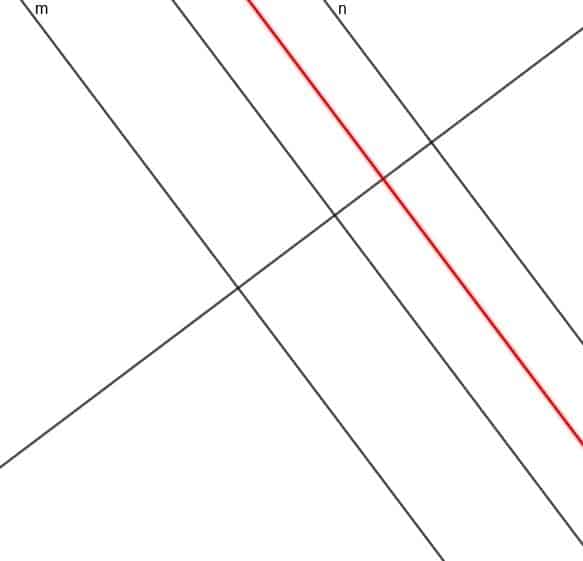
Suppose we have a point A that is always equidistant from two parallel lines, $m$ and $n$. The fourth locus theorem tells us that the path traced out by A is a third parallel line, $l$ that is parallel to both $m$ and $n$ and is directly halfway between the two.
Locus Theorem 5
Given an angle, ABC, the locus of a point D that is always equidistant from the lines BA and BC and lies inside the angle is the angle bisector of ABC.
Locus Theorem 6
The sixth locus theorem is essentially an extension of the fifth locus theorem. If we have two lines, $m$ and $n$ that intersect at a point A, the locus of a point B that is always equidistant from $m$ and $n$ is a pair of perpendicular lines that intersect at A and bisect the four angles formed by $m$ and $n$.
Examples
This section will go over common problems related to the loci of points and their step-by-step solutions.
Example 1
Suppose C is a moving point that is always equidistant from two points, A and B. Then, suppose E is a moving point that is always equidistant from B and another point D. If A, B, and D lie on a line, what is the relationship between the loci of C and E?
Example 1 Solution
First, we construct a line with the points A, B, and D on it. We’ll space them so that A and D are different distances from B.
We need to construct a point C that is always the same distance from A and B. The point on the line that satisfies that constraint is the center of segment AB. As we know from the third locus theorem, point C will trace out a perpendicular bisector for AB.
Likewise, we can consider the point E that is always equidistant from B and D. From the third locus theorem, we know that E will trace out a perpendicular bisector for BD.
Since A, B, and D lie on a straight line, the two perpendicular bisectors will be parallel to each other. That is, the loci for C and E will be parallel lines.
Example 2
Construct the locus of a moving point A that is always equidistant from two parallel lines $m$ and $n$.
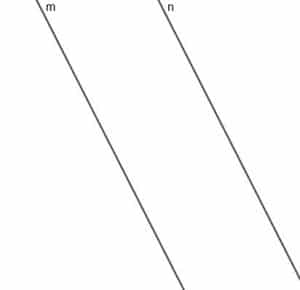
Example 2 Solution
The locus of this point will be a line that is parallel to $m$ and $n$, and the line of shortest distance from any point on this line to $m$ or $n$ will be the same length.
To construct this line, we first need to construct a line perpendicular to $m$, which will also be perpendicular to $n$.
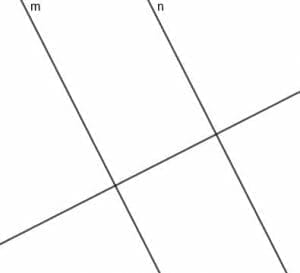
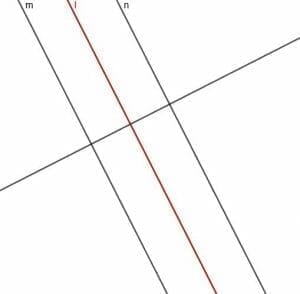
Now, we can construct a perpendicular bisector for the segment that connects $m$ and $n$. Since this line is perpendicular to a line perpendicular to $m$ and $n$, this line will be parallel to the two original lines.
Since this line bisects and segment perpendicular to $m$ that intersects $n$, it is always equidistant from the two lines, as required.
Example 3
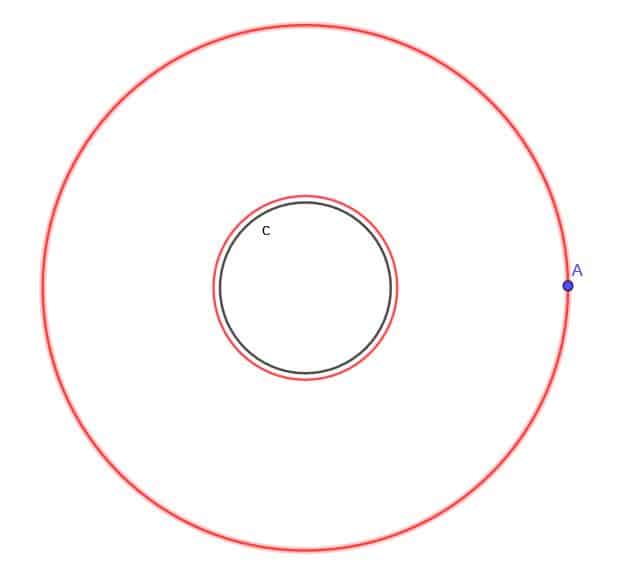
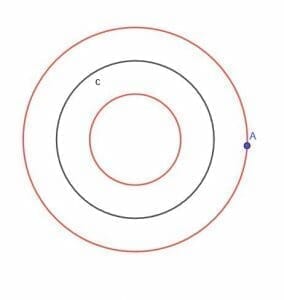
Given the circle, $c$, find the locus of a moving point A that is always at a distance $k$ from $c$, where $k$ is less than $r$, the circle’s radius.
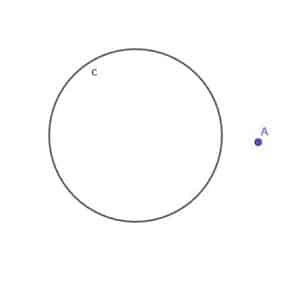
Example 3 Solution
Recall from the second locus theorem that the locus of a point that is always equidistant from a line traces out two lines parallel to the original. Each will be on the opposite side of the line and be at the same distance from it.
We can apply a similar concept here. First, outside the circle, we will have another circle with the same center as the first and a radius $r$+$k$. Thus, every point on this larger circle will have a distance $k$ from the original circle.
We will also construct a circle inside the original circle with the same center and a radius of $r$-$k$, which we know is greater than zero.
Example 4
Given the curved line $m$, shown, construct the locus of a moving point that is always equidistant from $m$.
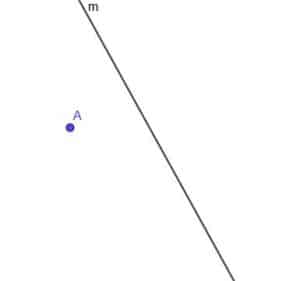
Example 4 Solution
First, we need to construct a line perpendicular to $m$ at point A. Recall that we do this by connecting A to any point on $m$. Then, we copy the angle that this new line makes with $m$ and construct a line that goes through A and makes the two congruent angles alternate angles.
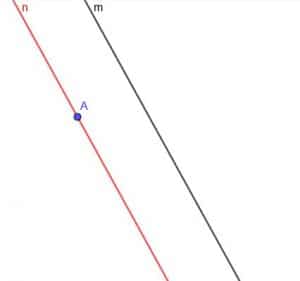
However, recall from locus theorem 2 that the locus will actually be two lines on opposite sides of the line $m$.
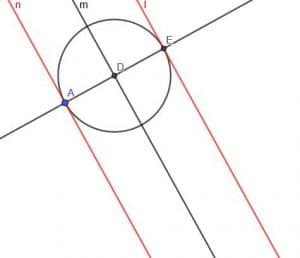
Now, we need to construct a line perpendicular to the line $n$. Label the intersection of the perpendicular line and \$m\$ as D.
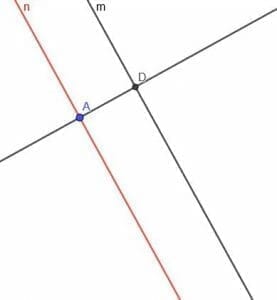
Now, construct a circle with center D and radius DA. Call the second intersection of the perpendicular line and this circle E.
Finally, we create a second line parallel to $m$ that goes through point E. We can do this as before, or we can create a line perpendicular to the perpendicular line at point E.
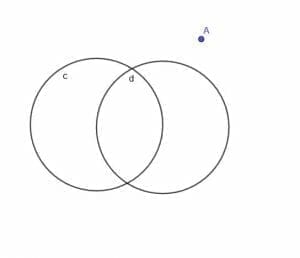
Example 5
Find the locus of a moving point A that is always a distance $k$ from one of the two circles, $c$ and $d$, and A is always outside the circles.
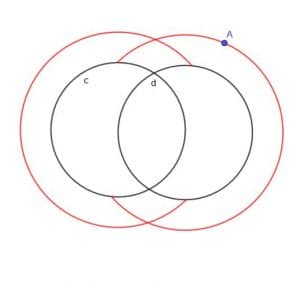
Example 5 Solution
If it were not specified that A was outside the two circles, the locus would essentially be two larger overlapping circles and two smaller overlapping circles.
However, since A is specified to be on the outside, we will not have the smaller inner circles. Nor will we have any parts of the larger circles that would have fallen inside either $c$ or $d$.
Therefore, the shape we get looks like a regular C and a backward C overlapping, as shown.
Practice Questions
![]()
Open Problems
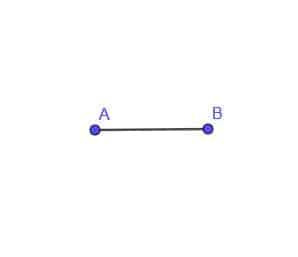
- Construct the locus of a moving point C that is always a distance AB from point A.

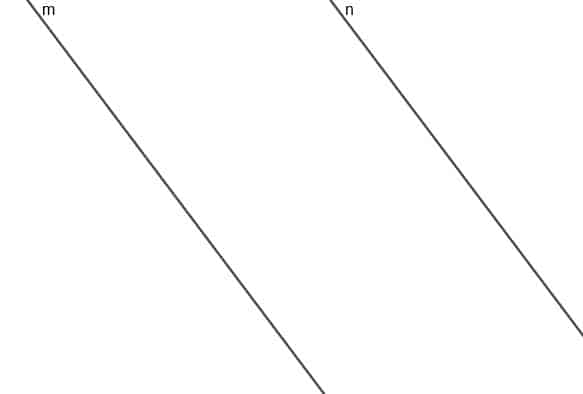
- Construct the locus of a point whose distance from the line $m$ is always three times the distance from the line $n$.

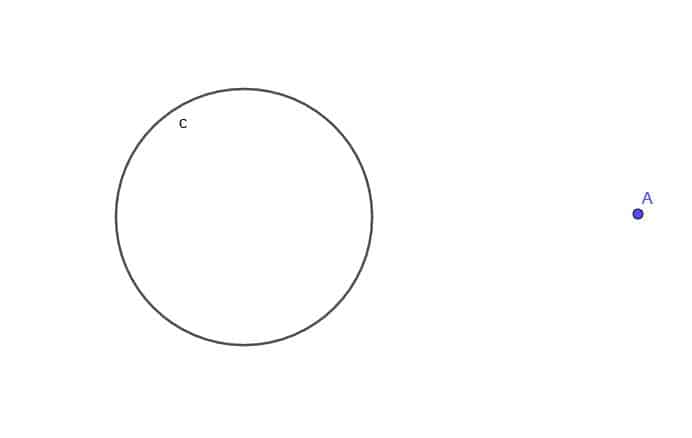
- Given the circle, $c$, find the locus of a moving point A that is always at a distance $k$ from $c$, where $k$ is greater than $r$, the circle’s radius.

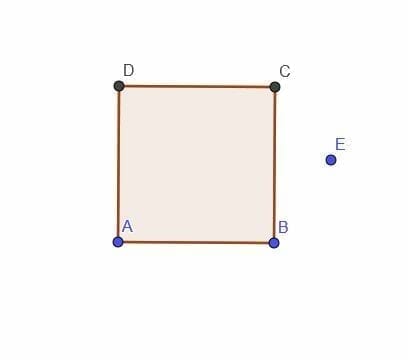
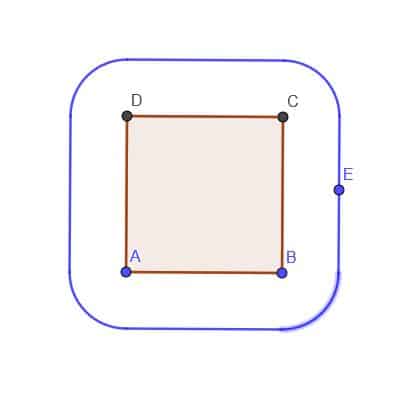
- Given a square ABCD, construct the locus of a point E that is always outside the square at a distance $k$. Assume $k$ is less than AB.

- Is it possible that the locus of a moving point does not exist? Can you think of an example and explain why it works?
Open Problem Solutions




- Yes, it is possible. For example, assume we want to find the locus of a moving point that is always equidistant from three points in a scalene triangle. The circumcenter of the triangle would work, but there would not be a smooth path for the point to move along from there.
Images/mathematical drawings are created with GeoGebra.