JUMP TO TOPIC
Absolute Value Calculator + Online Solver With Free Steps
An Absolute Value Calculator is an online tool that can solve mathematical equations involving absolute values. The calculator takes the equation as its input.
The calculator solves the equation by providing the graph, integer values of the solution, and their number line representation.

What Is the Absolute Value Calculator?
The Absolute Value Calculator is an online tool that can be used to find solutions to absolute value equations quickly.
Equations with variables inside the absolute operator (modulus) are known as absolute value equations. These equations are frequently used in many real-life problems like calculating distance, determining range, finding the variation, etc.
That’s why these equations have deep roots in the fields of calculus, engineering, and communication. The absolute operator gives the non-negative values of the input. These equations are solved by equating them to negative and positive constants separately.
Equations with absolute operators are easier to solve. Although you can solve them at the speed of knots using the Absolute Value Calculator. It solves any kind of complex absolute value equations quickly by providing you with the exact solutions.
Unlike other advanced tools, this calculator is free as you don’t have to buy a subscription. It works in your browser and does not require any downloading and installation. Anyone can use this calculator anytime by connecting to the internet.
The calculator is reliable and efficient as it provides you with the most accurate and precise solutions. Everyone can easily use it and move around the tool, which makes its user interface highly friendly.
To know further regarding the calculator’s usage and working principle, check the upcoming sections.
How To Use the Absolute Value Calculator?
You can use the Absolute Value Calculator by entering several mathematical equations with absolute terms. Enter the equation, click the button and the calculator performs the rest of the processing to provide you with a detailed solution.
The calculator’s interface is very simple to understand. The calculator has only one empty box for taking the input equation and a button for acquiring the solution. Once you have a valid absolute value equation you are ready to use this tool.
Follow the short and simple procedure given below to use the calculator correctly.
Step 1
Enter the absolute value equation of your problem in the Evaluate box.
Step 2
Then for obtaining the final answer, press the Submit button.
Result
The result of every problem is a comprehensive solution with multiple parts. The first part is input interpretation where the user can confirm whether the input is correctly inserted.
The next part is the plot which provides a graph of the absolute value equations. It describes how the equation looks in the cartesian plane. Then the number line represents the values in a single plane of the unknown variable.
At the last, it provides the integer solutions that are actual numeric values of variables obtained after solving the absolute value equations.
How Does the Absolute Value Calculator Work?
This calculator works by evaluating the absolute value equation and returning the equation’s plot and its representation on the number line. The knowledge of the absolute value is essential for understanding the functionality of this calculator.
What Is the Absolute Value?
The value that represents the number’s magnitude regardless of its sign is called the absolute value of that number. This value will always be positive. The absolute value of the real number is only that number without considering its sign.
Therefore, the absolute value of a positive real number is the number as it is and the value of a negative real number is also that number but without its negative sign. The absolute value of zero is always a zero.
The absolute value of any number x is given by:
\[
|x|=
\begin{cases}
-x,& \text{if } x < 0\\
x,& \text{if } x \geq 0
\end{cases}
\]
The absolute value of a number is the distance of that number from the origin in the light of the geometric definition. The distance is always a positive quantity hence the absolute value is also a positive number.
What Is the Absolute Value Function?
The absolute value function is the function in which the algebraic expression is inside the absolute value bars. This function is in the form of:
f(x)= a|x-h|+k
In the above function, ‘a‘ exhibits how much the function stretches vertically, ‘h‘ exhibits the horizontal shift and ‘k‘ represents the vertical shift. The above function is also known as the modulus function.
The value of h=0, k=0, and a=1 is often used for the absolute value function. This function is important in algebra.
The domain of this function is a set of all real numbers and it always produces positive numbers for any input value hence its range is the set of all non-negative real numbers.
To better visualize the absolute value function, let’s see their graph in the cartesian plane.
Absolute Value Functions
The absolute value function is given by f(x)= a|x-h|+ k. The graph of this function is ‘V-shaped means the graph opens upward if the value of a is positive or if the value is negative it is inverted ‘V-shaped means the graph opens downward.
The value of h and k provides the vertex of the graph. The absolute value function’s graph is shown below:
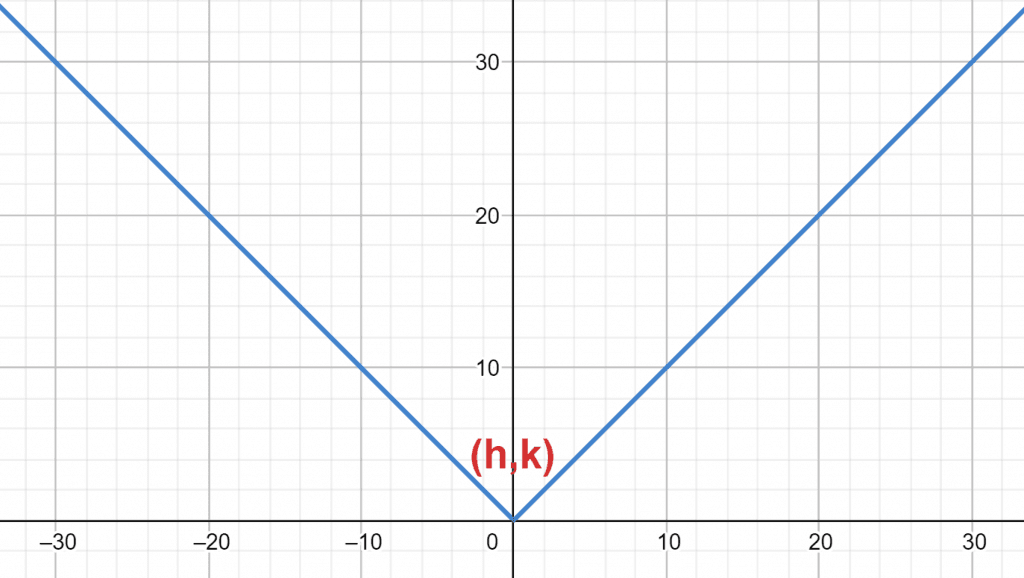
Figure 1
Solving Absolute Value Equation
The absolute value equations can be solved by applying the same algebraic techniques that are used to solve other equations. The equation for any unknown variable can be solved by first isolating the absolute value expression.
Subsequently, split the original equation into two equations, one equal to a positive quantity on the other side of the equation, and the second equal to a negative quantity. Then simplify for the unknown variable in both of the equations.
Finally, check the solution analytically or graphically. The absolute value equations have two solutions.
Applications of Absolute Value
The absolute value has many real-life applications. The absolute values are used by geophysicists to calculate the total amount of energy used because the direction of movement in an energy wave is both positive and negative.
The scuba divers with the help of these values detect their location with respect to the sea level such as they use to perceive “100 meters below sea level” instead of perceiving -100 meters.
The distance measurement is one of the most common applications of absolute values. The difference in position between the two points is equal to the absolute value of the distance.
These values are used for the distance when there is no need to represent the direction because the distance is not confided in with the direction.
The absolute values have also applications in money transfers. The number of money transferred when the debt is paid is always positive.
These values are also helpful to detect the deviation of a value from the average. For instance, the absolute value equal to zero means that the value is equal to the average however the value is far from the average if the absolute value is very high.
Solved Examples
There are some solved problems by the Absolute Value Calculator. Let’s discuss them in detail one by one to further clarify our concepts.
Example 1
Mike’s walkie-talkie has a range of 3 miles. He is traveling on the highway and is currently at a mile marker 18 miles from the initial point. The expression for the range calculation is given below:
|x – 18| = 3
Find the maximum and minimum range his walkie-talkie can cover from the current point.
Solution
The solution to the problem is given in some steps.
Integer Solution
The numerical values of variable x are given as:
x = 15 and x = 21
Plot
The graph for the equation|x – 18| = 3 is shown in figure 2. Here the two red points are the intersection of both the equations.
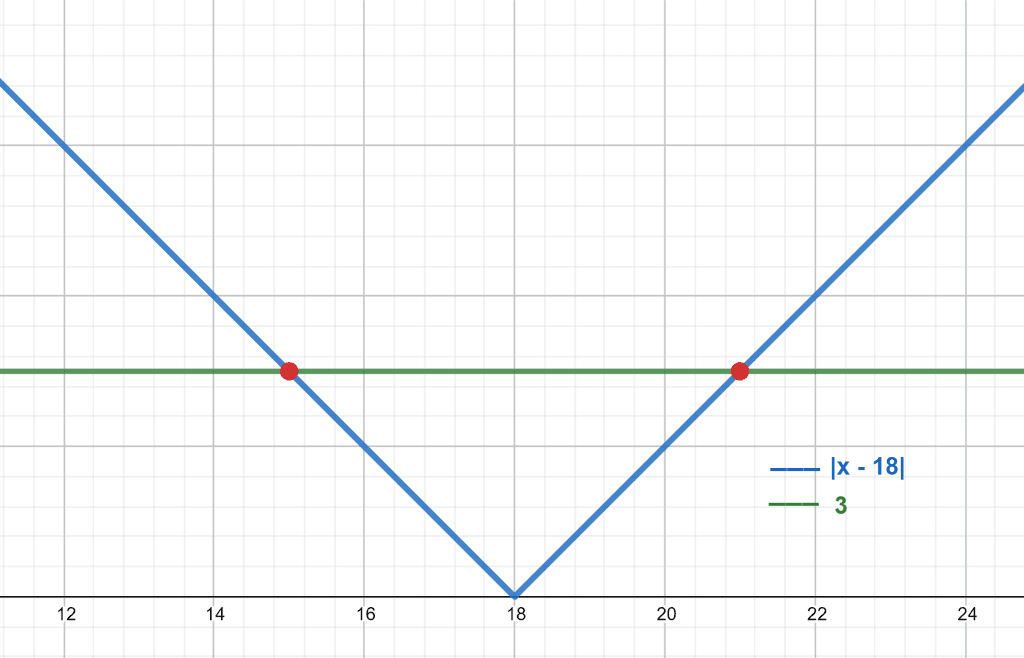
Figure 2
Number Line
Both values of variable ‘x‘ are represented in the x-plane which can be seen in figure 3.

Figure 3
Example 2
A geophysicist is assigned to a project given by the department of geosciences. The project is to look at the total amount of energy used in an energy wave. He wants to solve the absolute value equation to calculate this energy. The equation is given by:
2|5x-1|= 12
Solution
The above equation can be solved by inserting it into the absolute value equation calculator.
Integer Solution
x= -1 and x= $\frac{7}{5}$
Plot
The graph for the given equation is demonstrated below in figure 4.
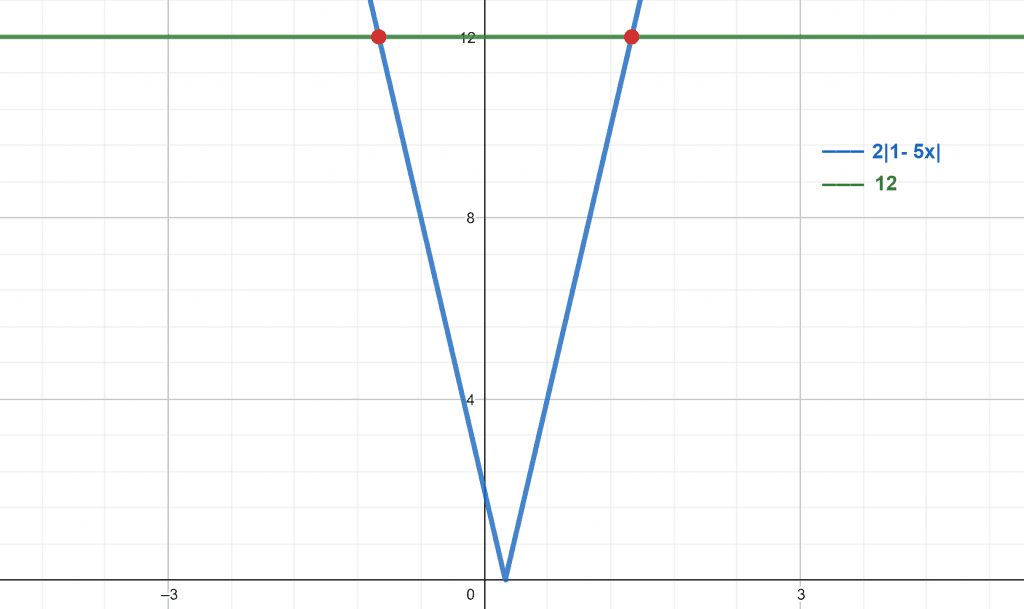
Figure 4
Number Line
The obtained solution is represented on the number line by two filled-in circles.

Figure 5
Example 3
Consider the below-given absolute value equation. Solve this equation to find the values for x.
|2x + 1| = 9
Solution
Integer Solution
First, the values for x are determined which are given below.
x = -5 and x = 4
Plot
The equation is plotted in the x-y plane which can be seen in figure 6.
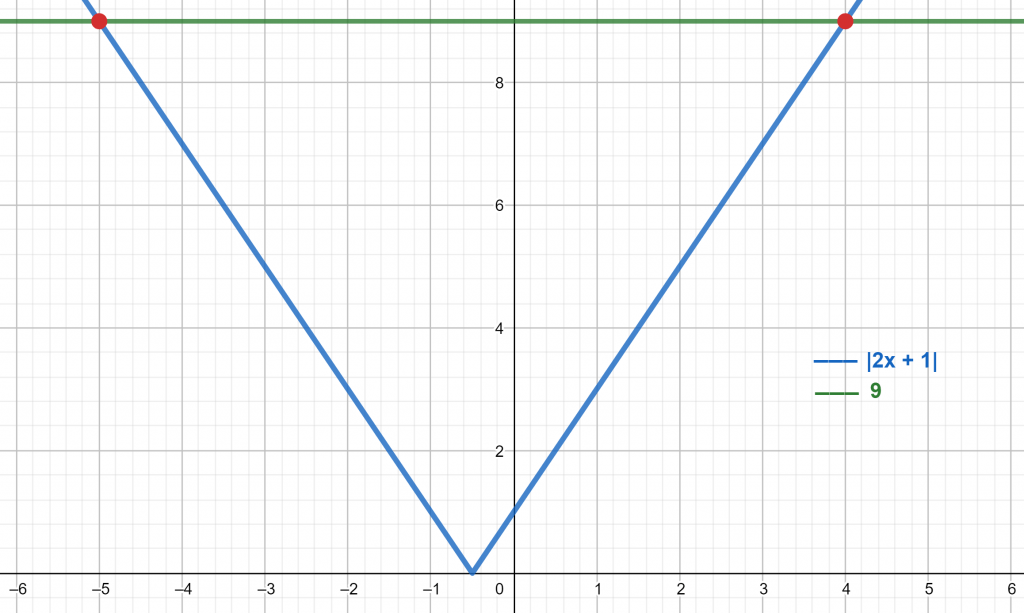
Figure 6
Number Line
Figure 7 plots the values obtained in a single x-plane.

Figure 7
All the Mathematical Images/Graphs are created using GeoGebra.
