JUMP TO TOPIC
Alpha Calculator + Online Solver With Free Steps
An Alpha Calculator or Algebra Calculator is used for easily finding all the possible solutions to a given equation. Any type of equation can be entered into the calculator.
The results display the simplified solution as well as the plot, domain, range, roots, differential, integral, polynomial, alternate, and complex form of the input equation.

What Is an Alpha Calculator?
An Alpha Calculator is an online calculator that can be used to determine the solution to all types of equations with the press of a button.
It can be used to obtain a step-by-step solution of any type of equation, be it arithmetic, differential, inequality, or an algebraic equation.
It helps in developing a plot of the given function and tells what the graph appears to be like in the x-y plane. The plot can be two-dimensional and three-dimensional based on the type of equation entered into the calculator.
How To Use an Alpha Calculator
You can start using the Alpha Calculator by performing the following steps:
Step 1
Start by setting up an equation that you want to solve using the Alpha Calculator.
Step 2
Enter the type of equation in the input box labeled as Equation.
Step 3
After that, click the Submit button, located below the box, to view the solution.
Step 4
The Result window will appear in front of you after clicking the submit button.
The following solutions will appear on the output screen:
Input
The first block titled Input displays the function entered by you as input. The function is displayed as it is.
Plot
The block titled Plot shows a graph of the input function that is plotted in the x-y plane or the x-y-z plane. The plot can be two-dimensional or three-dimensional.
Geometric Figure
The space given in front of the title Geometric Figure shows the type of figure plotted as a result of the entered function. It can be a line, hyperbola, ellipse, or any three-dimensional figure.
Root
The next block gives the roots of the equation. It is the value of the variable that satisfies the input equation.
The results further display the properties of the input function as a real function whose range lies between the real numbers. These properties are as follows:
Domain
This block displays the domain of the function. It is those inputs that are allowed to be entered into the function.
Range
In the space below Range, the range of the given function is displayed. The range consists of all the values possibly obtained as a result when the domain is entered into the function.
Bijectivity
This block shows whether the input function is injective or bijective.
Differential
The results also show the differential of the function and answer in the form of a numerical value.
Indefinite Integral
This block shows the integral of the given function and a numerical answer is calculated.
Some other results that the Alpha Calculator displays based on the type of function entered are:
Alternate Form
An alternate form of the given function is displayed in simple or complex variable form.
Polynomial Discriminant
In this space, the part of the Quadratic Formula $b^2 -4ac$, which is called Discriminant, is used to show the answer in a numerical value.
Parity
Parity shows whether the given function is even or odd.
Global Minimum
It displays the smallest value on the graph of the function.
Global Maximum
It shows the largest value of the function on the graph.
Step 5
If you would like to keep using the calculator to solve any other equation, just simply input the data and keep solving.
Various types of equations can be solved by using the same method with the help of the Alpha Calculator.
How Does an Alpha Calculator Work?
An Alpha Calculator works by providing all the possible types of solutions to the equation entered as input. The problem is entered into the calculator and all the available solutions to the problem equation are displayed.
The Alpha Calculator is also used to determine the domain and range. Moreover, it also tells about the bijectivity or injectivity of the function. In addition to that, the alpha calculator is also used to determine the derivative, partial derivative, and indefinite integral of the given function.
It provides the roots of the function. The calculator also provides the parity of the function and shows if the function is even or odd. The Alpha Calculator also provides an alternate form of the input equation, which can be in simple or complex form. Apart from that, the polynomial discriminant is also displayed on the output screen.
It simplifies the given equation and displays the value of the variable in numerical form. An Alpha Calculator also provides the global minimum and global maximum of the function.
The function or equation is entered into the calculator and all the answers are displayed on the screen. Therefore, the Alpha Calculator can be used to seek the solution to all forms of algebraic equations efficiently and quickly.
Solved Examples
Example 1
Solve the following equation using an Alpha Calculator:
y=2x + 1
Solution
The solution is displayed as follows:
Input:
y=2x+1
Plot:
The plot of the straight line is given in figure 1 as:
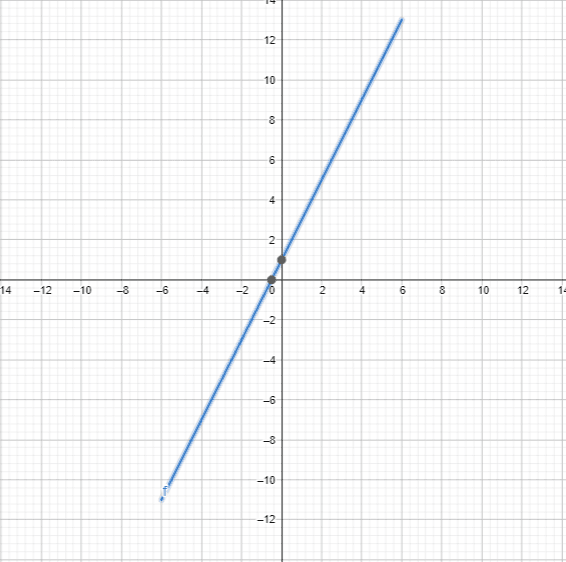
Figure 1
Geometric Figure:
Line
Root:
x= -1/2
Domain:
$\mathbb{R}$ (all real numbers)
Range:
$\mathbb{R}$ (all real numbers)
Alternate Form:
-2x+y-1=0
Bijectivity:
Bijective (from its domain to $\mathbb{R}$)
Partial Derivatives:
\[ \dfrac{\partial(2x+1)}{\partial(x)} = 2 \]
\[ \dfrac{\partial(2x+1)}{\partial(y)} = 0 \]
Example 2
Solve:
3x = 4y + 1
Using an Alpha Calculator.
Solution
The solution is given as follows:
Input:
3x = 4y + 1
Plot:
The plot of the straight line is shown in figure 2 as:
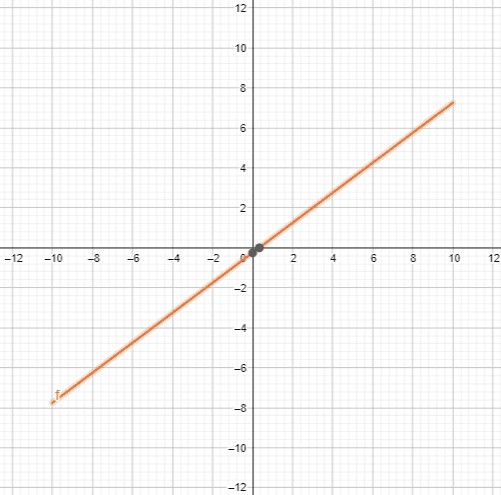
Figure 2
Geometric Figure:
Line
Alternate Form:
\[ x = \dfrac{4y}{3} + \dfrac{1}{3} \]
3x – 4y – 1 = 0
Real Solution:
\[ y = \dfrac{3x}{4} – \dfrac{1}{4} \]
Integer Solution:
x = 4n + 3
y = 3n + 2
where, $n \in \mathbb{Z}$.
Solution for the Variable y:
\[ y = \dfrac{1}{4}(3x-1) \]
Example 3
For the given Equation:
\[ y = x^2 \]
Use the Alpha Calculator to attain the solution.
Solution
Input:
\[ y = x^2 \]
Plot:
The graph of this parabola equation is shown in figure 3:
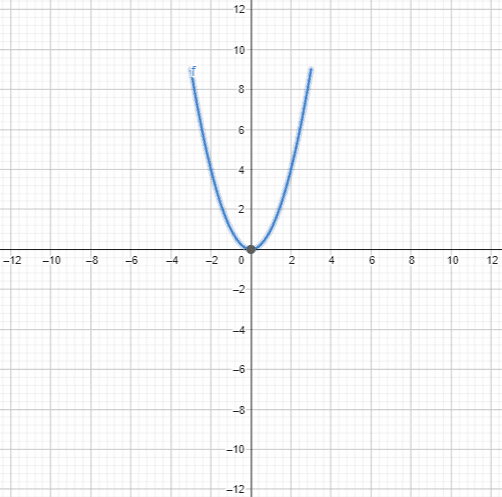
Figure 3
Geometric Figure:
Parabola
Alternate Form:
\[ y-x^2 = 0 \]
Root:
x = 0
Domain:
\[ x \in \mathbb{R} \]
Range
\[ y \in R : y\geq0 \]
Parity:
Even
Partial Derivative:
\[ \dfrac{\partial(x^2)}{\partial(x)} = 2x \]
\[ \dfrac{\partial(x^2)}{\partial(y)} = 0 \]
Implicit Derivatives:
\[ \dfrac{\partial{x(y)}}{\partial(y)} = \dfrac{1}{2x} \]
\[ \dfrac{\partial{y(x)}}{\partial(x)} = 2x \]
Global Minimum:
Global minima is given as:
\[ min{(x^2)} = 0\]
at x=0.
All the Mathematical Images/Graphs are created using GeoGebra.
