JUMP TO TOPIC
Curvature Calculator + Online Solver With Free Steps
The curvature calculator is used to calculate the measure of bend at a given point in any curve in a three-dimensional plane. The smaller the circle, the greater the curvature and vice versa.
This calculator also computes the radius, center, and equation of the osculating circle and plots the osculating circle in a 3-D plane.

What Is a Curvature Calculator?
The curvature calculator is an online calculator that is used to calculate the curvature k at a given point in the curve.
The curve is determined by the three parametric equations x, y, and z in terms of variable t.
It also plots the osculating circle for the given point and the curve obtained from the three parametric equations.
How To Use Curvature Calculator
You can use the curvature calculator by following the steps given below:
Step 1
Enter the first parametric equation which is in the form of (x,t). The user enters this first equation in the first block against the title “Curvature of (” on the calculator. This equation is a function of t by default. The function set by default is cost.
Step 2
Enter the second parametric equation which is in the form of (y, t). The user enters it in the second block against the title “Curvature of (” displayed on the calculator layout. The function set by default is sint, which is a function of t.
Step 3
The user enters the third parametric equation which is in the form of (z, t). It should be entered in the third block of “Curvature of ( ” on the calculator. The third equation set by default by the calculator is t.
Step 4
The user should now enter the point on the curve for which the curvature needs to be calculated. The calculator shows the tab at t in which it should be entered.
Step 5
Press the submit button for the calculator to process the entered input.
Output
The calculator will show the output in the four windows as follows:
Input Interpretation
The input interpretation shows the three parametric equations for which the curvature needs to be calculated. It also shows the value of t for which the curvature is required.
The user can confirm the input from this window. If the input is incorrect or some information is missing, the calculator gives the signal “Not a valid input, please try again.”
Result
The result shows the value of curvature for three parametric equations in the x-y-z plane. This value is specific to the point for which the curvature is to be determined.
The curvature k is the reciprocal of the radius of curvature 𝒑.
So,
\[ k = \frac{1}{𝒑} \]
Osculating Sphere
This window shows the following three outputs required to plot the osculating sphere.
Center
By putting the value of x=0, y=0, and z=0 in the obtained equation, the osculating sphere’s center is calculated.
Radius
The radius of curvature, denoted by 𝒑, is calculated by the following formula:
\[ 𝒑 = \frac{{[ (x’)^2 + (y’)^2 ]}^{\frac{3}{2}}}{ (x’)(y’’) – (y’)(x’’) } \]
Where:
$x’$ is the first derivative of $x$ with respect to $t$.
\[ x’ = \frac{dx}{dt} \]
y’ is the first derivative of y with respect to t.
\[ y’ = \frac{dy}{dt} \]
x’’ is the second derivative of x with respect to t.
\[ x’’ = \frac{d^2 x}{d t^2 } \]
y’’ is the second derivative of y with respect to t.
\[ y’’ = \frac{d^2 y}{d t^2 } \]
The radius of curvature is the distance from a point on the curve to the center of curvature.
Equation
The equation of an osculating sphere is obtained by the point of the center of curvature placed into the equation of a sphere.
Plot
The plot shows the point at which the curvature is calculated. The point makes the osculating circle by the obtained circle equation.
The blue curve shows the three parametric equations combined in the Cartesian form to be plotted in a 3-D plane.
Solved Examples
Here are some solved examples of the curvature calculator.
Example 1
Find the curvature for ( 2cos(t) , 2sin(t), t ) at the point:
\[ t = \frac{π}{2} \]
Also, evaluate the center, radius, and equation of curvature for the above three equations.
Plot the osculating circle in the 3-D plane.
Solution
The calculator interprets the input and displays the three parametric equations as follows:
x = 2cos(t)
y = 2sin(t)
z = t
It also displays the point for which the curvature is calculated. So:
\[ t = \frac{π}{2} \]
The calculator computes the result by putting the values of x, y, and z in the equation of curvature.
The value $(t = \dfrac{π}{2})$ is put in the equation of curvature and the result comes out to be:
\[ Curvature = \frac{2}{5} \]
The osculating sphere window shows the following results.
\[ Center = \Big\{ 0 , \frac{1}{2} , \frac{ -π }{2} \Big\} \]
\[ Radius = \frac{5}{2} \]
Note that the radius of curvature is the reciprocal of curvature.
The equation comes out to be:
\[ Equation = x^2 + { \Big\{ \frac{1}{2} + y \Big\} }^2 + { \Big\{ \frac{ -π }{2} + z \Big\} }^2 \]
By putting the value of t in x, y, and z and then substituting the resulting x, y, and z in the above equation, it will give us $\dfrac{25}{4}$.
The following figure 1 shows the osculating circle for which the curvature is calculated.
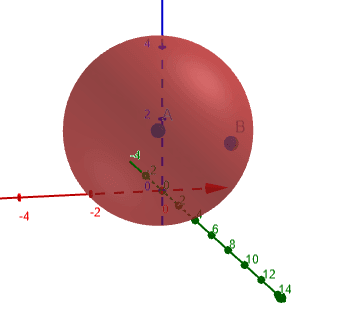
Figure 1
Example 2
Compute the curvature for ( cos(2t) , sin(3t) , t ) at the point:
\[ t = \frac{π}{2} \]
Also, compute the center of curvature, radius of curvature, and the equation of curvature for the above three equations. Plot the osculating circle at the given point in the 3-D axes.
Solution
The calculator displays the input interpretation of the three parametric equations as follows:
x =cos(2t)
y =sin(3t)
z = t
The point for which the curvature is required is also displayed as follows:
\[ t = \frac{π}{2} \]
Now, the result is computed by putting the values of x, y,and z in the equation of curvature. The value of $(t = \dfrac{π}{2})$ is placed in the curvature equation.
It displays the result as follows:
\[ Curvature = \sqrt{97} \]
The osculating sphere window shows the center as:
\[ Center = \Big\{ \frac{-93}{97} , \frac{-88}{97} , \frac{π}{2} \Big\} \]
The radius is:
\[ Radius = \frac{1}{ \sqrt{97} } \]
The equation becomes:
\[ Equation = \Big\{ \frac{93}{97} + x \Big\}^2 + \Big\{ \frac{88}{97} + y \Big\}^2 + \Big\{ \frac{-π}{2} + z \Big\}^2 \]
Putting the resulting values of x, y and z in the above equation after placing the value of t in x, y and z gives us $\dfrac{1}{97}$.
The following graph in figure 2 shows the osculating circle at the given point.
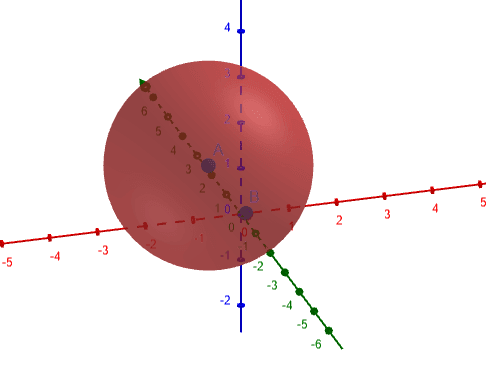
Figure 2
All the Mathematical images/Graphs are created using GeoGebra.
