JUMP TO TOPIC
Arc Length Calculator Calculus + Online Solver With Free Steps
The Arc Length Calculator is a tool that allows you to visualize the arc length of curves in the cartesian plane. The calculator takes the curve equation and interval limits as input to calculate the results.
Arc length is a particular portion of a curve between two specified points. It is further used in determining the surface area of the curve. The calculator will display the arc length of the given equation in the x-y plane.

What Is an Arc Length Calculator?
An Arc Length Calculator is a handy online calculator that can be used to figure out the arc length of the curves the input function produces within a given interval.
Arc Length holds great significance because the daily challenges that engineers and mathematicians encounter typically involve various types of curves. For instance, performing calculations for the construction of bridges and roads in the city.
It takes time to find and draw the arc length of any curve if solved manually. But the Arc Length Calculator solves these problems quickly for you by giving accurate and precise solutions.
How To Use the Arc Length Calculator?
You can use the Arc Length Calculator by entering the different target functions in the calculator. Due to its simple and friendly interface, everyone can operate this tool on their device.
An interesting feature about this calculator is that it is not limited to only one type of function. It can get arc length for any mathematical function like algebraic, trigonometric, exponential, etc.
When you have a valid function and appropriate end-points of the intervals, you can play with this calculator to resolve your problem. The step-by-step procedure to operate this calculator is given below.
Step 1
Put the mathematical function in the Equation field. It is the function that expresses the curve for which you want to calculate the arc length.
Step 2
Now you need to enter the duration of your interval. Put the starting point in the Beginning Interval tab while the endpoint in the End Interval tab.
Step 3
At the last, press the Submit button to get the final result.
Result
The result will be a graph of the input function. It displays the arc length specified in a straight bold line with highlighted endpoints. The rest of the function is represented with a dotted line.
How Does the Arc Length Calculator Work?
This calculator works by finding the arc length of the continuous function on the given interval. This calculator accepts the upper and lower limit of the interval and then plots the arc length of the given function.
The working of the arc length calculator is based on the arc length theorem however to understand this theorem we should know the arc length of a function.
What Is the Arc Length?
The arc length of a function or length of the curve is defined as the total distance covered by a point along an interval [a,b] when it follows the graph of the continuous function.
An arc length is a powerful tool for our problem-solving techniques. This concept is not only used for mathematical applications but it can also be used for solving some real-life problems.
For instance, if the curve is used to represent the path of a moving object in space, then the length of the curve between two points is the distance the moving object covered between two times.
Similarly, if a rocket is launched in space along the parabolic path then arc length is used to calculate how far the rocket travels or if we are walking on a road to reach our desired destination then this length is used to find the distance to our destination point.
How To Calculate the Arc Length?
The arc length is calculated by the following formula:
\[Arc\:Length= \int_{a}^{b}\sqrt{1+[f'(x)]^2} \,dx\]
Where f(x) is a continuous function over the interval [a,b] and f’(x) is the derivative of function with respect to x.
This formula is derived on the basis of approximating the length of the curve. This approximation is done by dividing the curve into several segments. If each segment is considered as a straight line then by using the distance formula, the length of each line can be calculated.
The approximation for the total length of the curve can be found by adding all the lengths of each straight line in which the curve is divided. This approximation can be better by dividing the curve into a greater number of segments.
The arc length formula is in fact the simplified summation of distances of the straight lines calculated through the distance formula.
The function for which the arc length is calculated, that function should be differentiable and its derivative should be continuous. These types of functions are called smooth functions.
The above formula is defined for the function of x. If there is a requirement to find the arc length for the function of y, the same formula can be used except that the defined interval is now on the y-axis.
The arc length for the function of y is given below:
\[Arc\:length= \int_{c}^{d}\sqrt{1+[g'(y)]^2} \,dy\]
Where g(y) is the continuous function of $y$ over the interval [c,d] and g’(y) is the derivative of the function with respect to y.
Solved Examples
Let’s discuss some solved mathematical problems related to curves using Arc Length Calculator.
Example 1
A mathematician while doing research came across the following function:
\[ f(x) = \frac{4}{3} x^{3} \]
Now he needs to draw the arc length of the above function between a particular interval. The interval is given as:
x = [ -1, 1 ]
Solution
The solution to this problem can be easily obtained using Arc Length Calculator.
Plot
The given function is plotted in the x-y plane which can be seen in figure 1. The straight line indicates the arc length in the interval [-1, 1], and the remaining part is denoted by a dashed line.
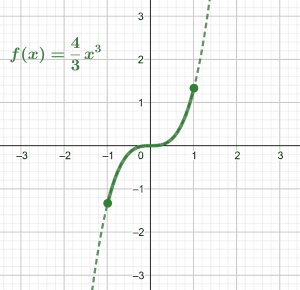
Figure 1
Example 2
A college student is presented with the following trigonometric equation.
f(x)=sin(2x)
He is asked to calculate the arc length for this function over the interval defined from 0 to 1.
Solution
The arc length for the above function can easily be calculated using the Arc Length Calculator by inserting the given function and defining the limits.
Plot
In the following figure, the arc length over the interval [0,1] is denoted.
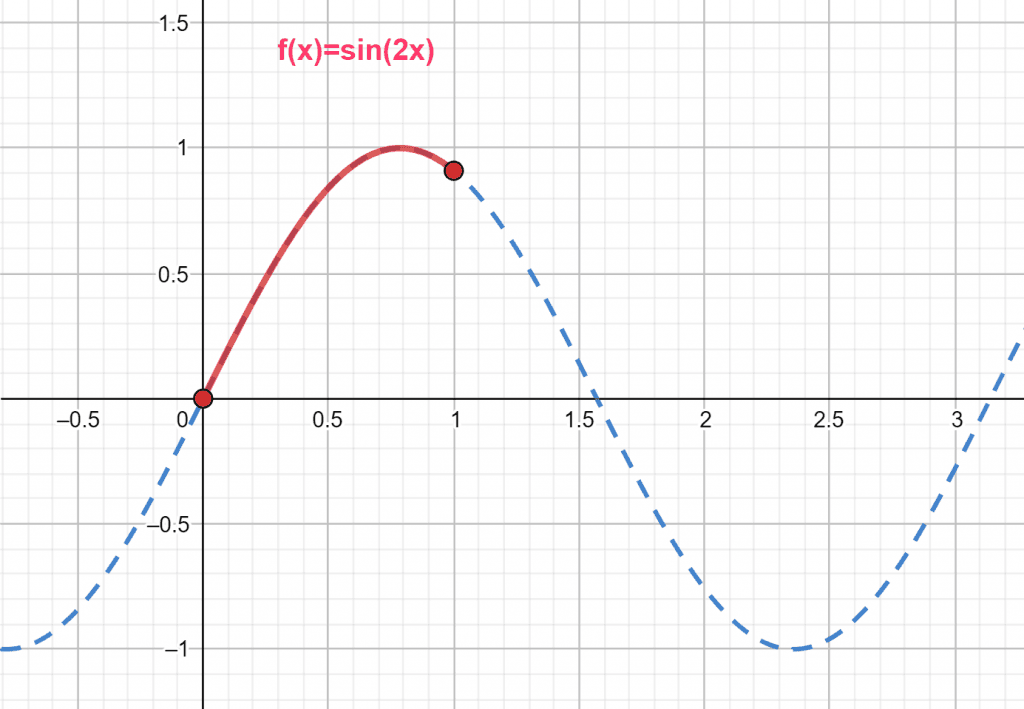
Figure 2
All the Mathematical Images/Graphs are created using GeoGebra.
