JUMP TO TOPIC
Center of Circle Calculator + Online Solver With Free Steps
The Center of Circle Calculator finds the equation of a circle given its center and either its radius or a point that lies on it.
What Is the Center of Circle Calculator?
The Center of Circle Calculator is an online tool that calculates the equation of a circle assuming two things are known: the circle’s center and either its radius or a point on its boundary.
The calculator interface consists of four text boxes in three rows, of which you must only fill three.
The first row has two text boxes side-by-side into which you must enter the coordinates of the circle’s center. In the left box, you enter the center’s x coordinate and its y coordinate in the one on the right. These two fields are mandatory in all cases.
The last two text boxes on the second and third rows are labeled “Through” and “Radius.” There is a selection circle next to these boxes – the calculator uses a different approach based on what you select. Make sure you leave the un-selected field empty, or the calculator will give errors.
If you choose Through, you need to enter the coordinates of the point through which the circle passes. For example, you could enter (3,8), (pi, pi/2), etc. It does not matter if you enter the coordinates with or without the round brackets, but make sure you separate the x and y coordinates with a comma.
If you choose Radius instead, you must only enter one number here; the circle’s radius. For example, you could enter 5, 10.198, 3/10, sqrt(pi), etc.
How To Use the Center of Circle Calculator?
You can use the Center of Circle Calculator to find the standard equation of a circle by entering the coordinates for its center and a point lying on it or its radius.
For example, suppose you want to find the area occupied by a circle of unit radius centered at the origin. Additionally, you also want the equation of the circle. You can use the calculator to get both of these by following the step-by-step guidelines below:
Step 1
Enter the coordinates for the center of the circle into the text boxes labeled “circle center (<field>, <field>)”. The first field takes the x coordinate, and the second the y coordinate.
For the mock example, you would enter “0” without quotes in both fields because the circle is on the origin, which has the coordinates (0, 0).
Step 2
Choose between “Through” and “Radius” by clicking on the selection circle next to the one you need to use. For the mock example, you would select the Radius option.
Step 3
If you chose Through in Step 2, enter the point coordinates in its text box and check that the Radius box is empty. If you went with Radius, enter the radius value into its text box and ensure the Through text box is empty.
Since you chose radius for the example, you would enter the value “1” without quotes in the text box labeled “Radius.”
Step 4
Press the Submit button to get the results.
Results
The results show in a pop-up dialogue window with four sections:
- Input Interpretation: This section shows the calculator’s interpretation of the input. It helps you manually verify that the calculator used your inputs correctly.
- Visual Representation: Here, you will see a 2D graph depicting the circle and the relevant points (center, radius, and the point lying on the circumference).
- Equation: This is the calculated equation of the circle in its standard form.
- Properties: Various properties of the circle appear here. These properties include its radius (if “Through” selected), diameter, circumference, etc.
The calculator shows the following results for the mock example.
Input Interpretation
| Circle | Center (0, 0) |
| Radius 1 |
Visual Representation
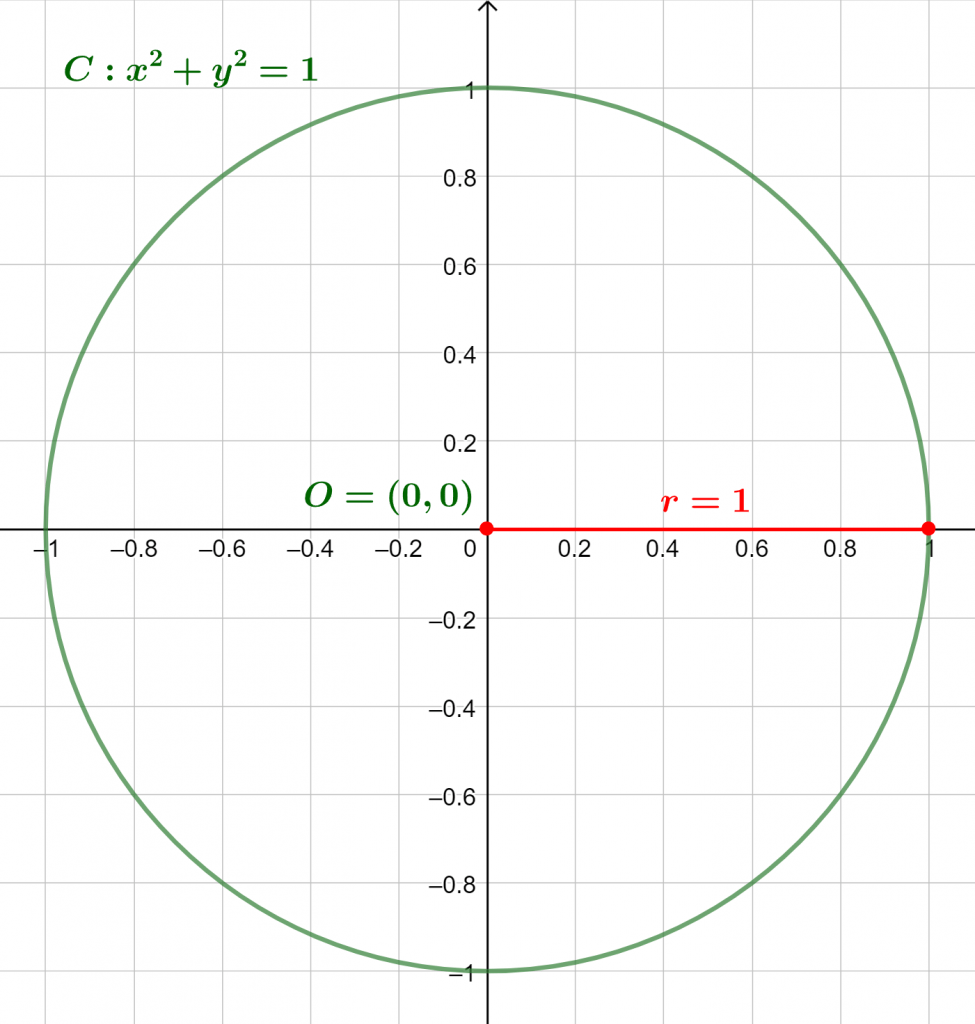
Figure 1
Equation
x$^\mathsf2$ + y$^\mathsf2$ = 1
Properties
| Diameter | 2 |
| Area enclosed | $\pi$ |
| Circumference | 2$\pi \approx$ 6.28319 |
| Centroid | (0, 0) |
| Curvature | 1 |
How Does the Center of Circle Calculator Work?
The Center of Circle Calculator works by calculating either the equation or the properties based on the input. Let us look at how it calculates the circle’s equation and properties in detail.
Calculating the Equation
The standard equation of a circle has the form:
(x – h)$^\mathsf2$ + (y – k)$^\mathsf2$ = r$^\mathsf2$
Where (h, k) are the coordinates for the center of the circle, and r is the radius. Any point (x, y) that satisfies this equation lies on the circle. When we say “on the circle,” we mean the circle’s boundary, also called its circumference.
What if the radius is unknown? If we know the coordinates of a point (a, b) that lies on the circle, we can calculate the radius using the distance formula:
\[ r = \text{distance} = \sqrt{(a-h)^2+(b-k)^2} \]
That is essentially the square root of the standard equation of the circle with x = a and y = b.
Calculating the Properties
The diameter value is simply twice that of the radius:
d = 2 x radius = 2r, where radius = r = d / 2
The curvature of a circle is the reciprocal of a circle’s radius, so:
curvature = 1 / radius = 1 / r
Since we know that the constant pi = $\pi$:
$\pi$ = circumference $\div$ diameter
Then, the circumference of a circle is defined by the following equation:
C = 2 x pi x radius = 2$\pi$r
The area of a circle can be found with the following equation:
A = pi x radius squared = $\pi$r$^\mathsf2$
Solved Example
Example 1
Find the equation of a circle centered at (1, -2) and passing through the point (3, 8). What are the values of its circumference, area, and curvature?
Solution
Let the center be point O (1, -2) and the point on the circle be P (3, 8). The distance between the center and the point on the circle boundary can then be found with the distance formula:
\[ |OP| = \sqrt{(P_x-O_x)^2+(P_y-O_y)} = \sqrt{(3-1)^2+(8-(-2)^2} \]
\[ |OP| = \sqrt{2^2+10^2} = 2\sqrt{26} \approx \boldsymbol{10.19804} \]
Note that this distance is geometrically equal to the radius of the circle, so |OP| = r $\approx$ 10.19804. Therefore, using the known formulae with pi = 3.14159, we get:
circumference = 2 x 3.14159 x 10.19804 = 64.07612
area = 3.14159 x 10.19804$^\mathsf{2} \approx$ 326.7254
curvature = 1 $\div$ 10.19804 $\approx$ 0.098058
The circle’s plot is given below:
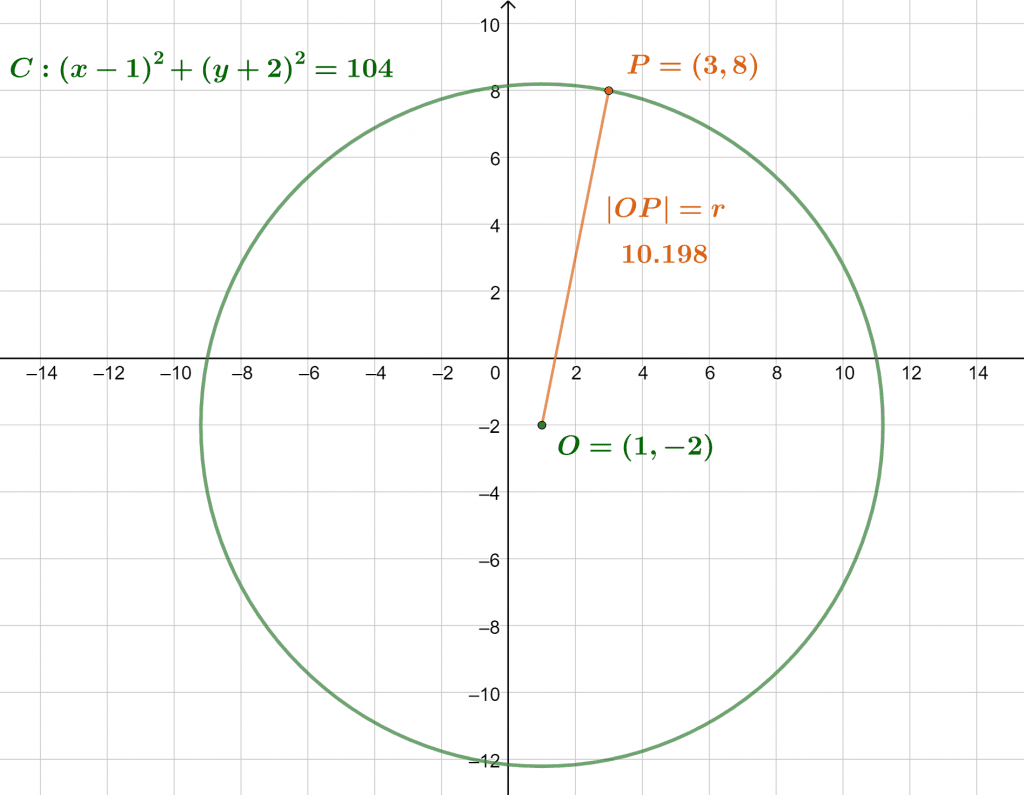
Figure 2
All graphs/images were created with GeoGebra.
