JUMP TO TOPIC
Kirchhoff Calculator
The online Kirchhoff calculator is a free tool that helps you find the values of current in a T circuit. There are three main parameters around which the calculations revolve; these are current, voltage, and impedance. The calculator takes the values of these parameters and, using Kirchhoff’s law, finds the values of currents.
Many real-life problems include circuit analysis, for which the concept of Kirchhoff’s law is important. Kirchhoff’s Laws determine the values of currents and voltages to solve real-life problems.
A basic rule needs to be followed for using Kirchhoff’s Law. It would help if you made some electrical analysis and mathematical manipulations to solve the circuits for the values of different components.
If you try to analyze a circuit by hand, it takes a lot of time and becomes even more time-consuming and complex for complex circuits. And a minor error can make your whole struggle useless.
So this online tool helps you analyze the circuit without fear of being wrong and time consumption and waste. You need to enter the correct values for the parameters of the circuit.

What Is the Kirchhoff Calculator?
The Kirchhoff Calculator is an online tool exclusively designed to analyze T circuits for the values of currents at nodes.
Kirchhoff’s law is one of the fundamental laws in the electrical domain for the analysis of circuits. The equations developed for the components of the circuit through Kirchhoff’s Law are used as the essential tool for starting the analysis of circuits.
This calculator solves any complex problem and finds the values of currents at nodes using Kirchhoff’s Law.
This calculator can be accessed through a good internet connection and browser. There is no need to purchase, download or install any application. It is one of the online tools available and can be used 24/7.
Method To Use the Calculator
You can use the Kirchhoff Calculator by putting the values of voltages and impedances in the provided boxes. Its detailed interface is very easy to understand. It is designed in a straightforward manner.
The calculator has six input boxes. The first two boxes are for the values of voltages, and the next three are for the values of resistances applied in the circuit. After putting these values in their respective boxes, you need to press a button o get the final solution to your problem.
You should follow the detailed step-by-step guide below to get the exact required solution from this tool.
Step 1
Insert the values of voltage sources in the first two boxes labeled V1 and V2.
Step 2
Now, Insert the values of impedances in the following three boxes labeled as Impedance R1, Impedance R2, and Impedance R3, respectively. Keep in mind that the values of impedance are in the SI unit.
Step 3
To get the final solution, click on Submit button.
Output
Once you press the Submit button, a small window opens in a new tab. This window contains the final result. The resulting interface has two sections. The first section contains the summary of input values under the title Input interpretation.
The second section is entitled Result. This contains the actual results, i.e., the values of currents in the circuit.
The Function of the Calculator
The Kirchhoff calculator works by finding the values of currents by applying Kirchhoff’s Current or Voltage Law. It calculates the unknown values of currents flowing in the electronic circuit.
Although this calculator is designed very simply and is easy to use, it will be better to use when there is basic knowledge about Kirchhoff’s law and basic circuit analysis techniques.
Following is a brief explanation of the basics of analyzing circuits using Kirchhoff’s law.
Kirchhoff’s Laws
Scientist Gustav Robert Kirchhoff presents two fundamental laws. These are Kirchhoff’s current law and Kirchhoff’s Voltage law.
Kirchhoff’s Current Law
Kirchhoff’s Current law states that the total current that enters a node is equal to the total current leaving the node. This law is also known by some other names like Kirchhoff’s First law and Kirchhoff’s Junction Rule. The current law is depicted in the following figure.
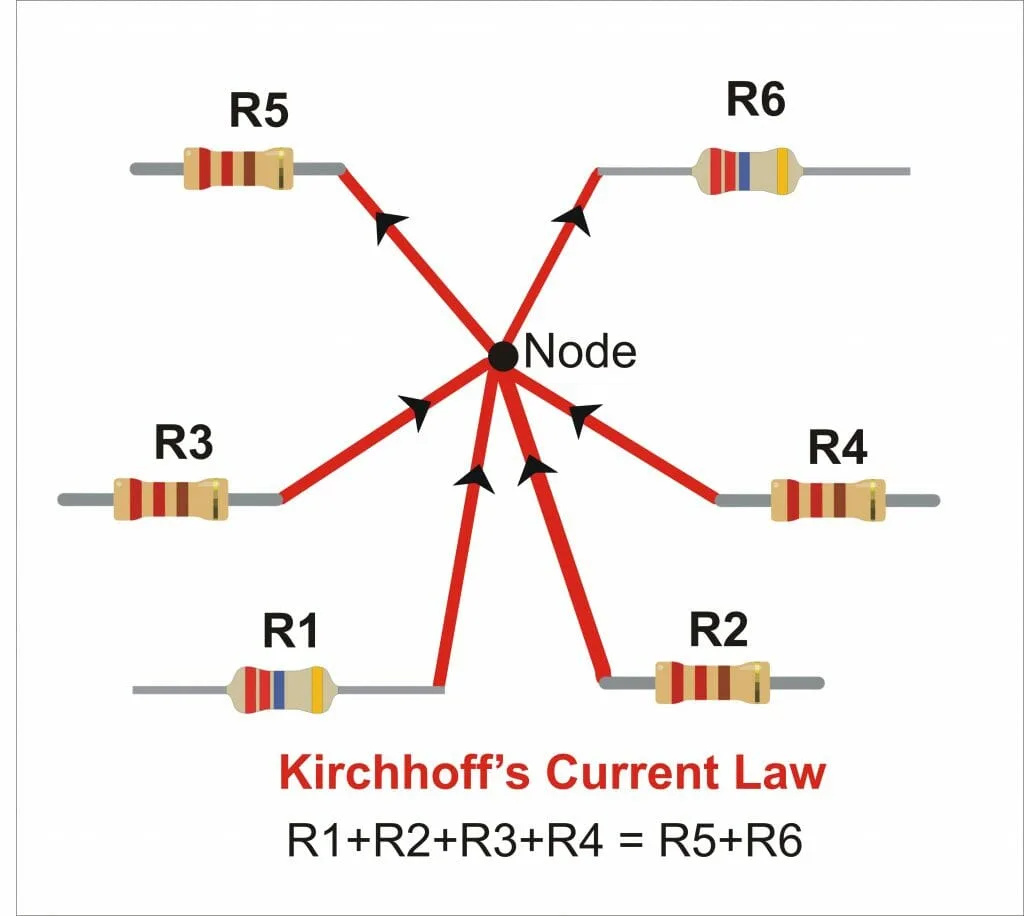
Figure 1
Kirchhoff’s Voltage Law
Kirchhoff’s voltage law states that the sum of all the voltage drops around the loop equals zero. This knowledge is known as Kirchhoff’s Second law or Kirchhoff’s loop law. Figure 2 shows the implementation of the voltage law.
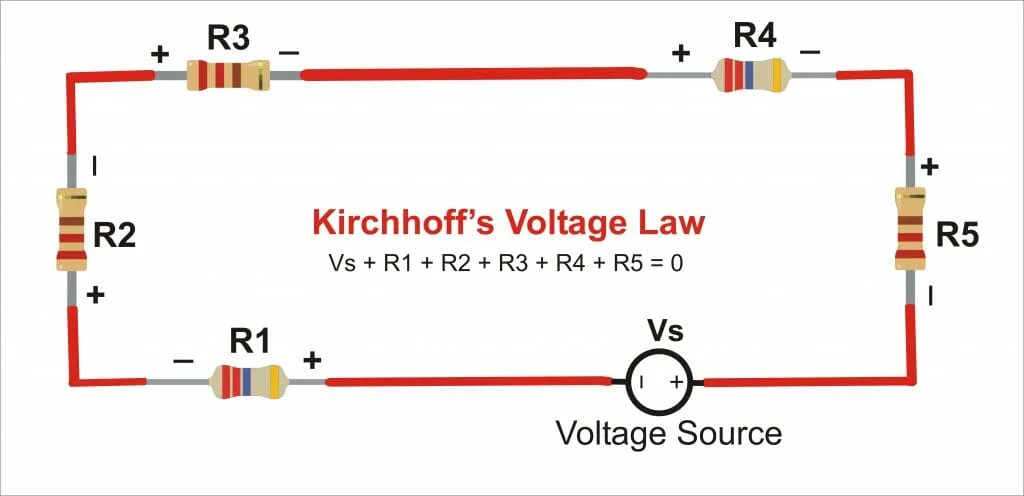
Figure 2
What Is a Node in a Circuit?
Nodes are the points in an electric circuit where the branches connect. These nodes are the bases of a very important circuit analysis technique known as nodal analysis.
Brief History of Kirchhoff’s Laws
German Physicist Gustav Kirchhoff developed Kirchhoff’s Laws in 1985. These laws deal with the conservation of energy and current in electronic circuits. There are two laws, and their name is associated with Kirchhoff’s name.
These laws proved to be very helpful in analyzing complex circuits and calculating the values of resistances and currents in these complex circuits.
Solved Examples
An excellent way to understand the tool is to solve the examples and analyze them. An example is described below that is solved using the Kirchhoff analysis T-circuit.
Example 1
In a circuit, you have to find all three currents (x=IA, y=IB, and z=IC) entering node VA. And voltages at V1= 40, V2= -30, and Impedance R1 = 30, R2 = 40, and R3 = 50.
Solution
Given:
V1 = 40
V2 = – 30
Impedance R1 = 30
Impedance R2 = 40
Impedance R3 = 50
The calculator uses Kirchhoff’s voltage law to drive equations.
c = 50
40 = 30(x) – c(z)
30 = -40(y) + c(z)
Now calculator reduces these simultaneous equations by subtraction to get the values of currents.
The calculator will give the result.
x = 1.085 Ampere
y = – 0.936 Ampere
z = 0.148 Ampere
So, the three currents entering node VA are x, y, and z.
Example 2
If the voltage connected in a series circuit is; Va = 20 V and Vb = 40 V. The resistance between node A and node B is 9 ohms, and the resistance connected at node B is 12 ohms. Find the currents flowing through both resistances.
Solution
The given details are:
Va = 20 V
Vb = 40 V
R1 = 9 ohm
R2 = 12 ohm
The currents are:
I1 = I2 = 1.05 A
