JUMP TO TOPIC
Exponential Growth Calculator + Online Solver With Free Steps
The online Exponential Growth Calculator is a tool that helps you find the sudden Growth in an equation.
The Exponential Growth Calculator is a valuable tool used by scientists and mathematicians to calculate exponential growth algorithms and diagrams.

What Is an Exponential Growth Calculator?
An Exponential Growth Calculator is an online tool that allows you to calculate the exponential growth of an equation.
The Exponential Growth Calculator requires four inputs: the left-hand side value of the equation, the two constant values to be multiplied, and a power value that indicates the rate of increase.
After adding the inputs, we click the “Submit” button on the calculator.
How To Use an Exponential Growth Calculator?
To use the exponential growth calculator, once all the inputs are entered into the calculator, we click the “Submit” button, which opens a new window and displays the results.
The detailed instructions on how to use an Exponential Growth Calculator can be found below:
Step 1
Initially, we input the left-hand side of our equation into the Exponential Growth Calculator.
Step 2
After we input the left-hand equation, we enter the “a” value obtained from the equation into the Exponential Growth Calculator.
Step 3
After we enter the “a” value, we proceed to enter the “b” value into the Exponential Growth Calculator.
Step 4
Once you are done with entering the “b” value, we enter the “x” value into the Exponential Growth Calculator.
Step 5
Finally, after entering all four input values into the calculator, we click the “Submit.” The Exponential Growth Calculator quickly calculates the exponential Growth of the equation and displays the results in a new window. The calculator also displays the type of equation, the roots, and a plotted graph of the equation.
How Does an Exponential Growth Calculator Work?
The Exponential Growth Calculator works by taking in all the inputs and calculating the exponential Growth of the equation. The Exponential Growth Calculator uses the following general equation to compute the exponential Growth:
\[ y = ab^{x} \]
Exponential Growth
In exponential Growth, a quantity starts slowly before increasing quickly. We apply the exponential growth formula when calculating population growth, compound interest, and doubling time.
Exponential Growth is a data pattern that illustrates an increase over time by generating an exponential function curve. Assume a cockroach population grows each year exponentially, starting with 3 in the first year, 9 in the second year, 729 in the third year, 387420489 in the fourth year, and so on.
In this example, the population grows by a factor of three per year. Exponents are used in the exponential growth formula, as the name implies. Exponential growth models involve some formulas. They are as follows:
\[ y = ab^{x} \]
\[ y = a(1 + r)^{x} \]
\[ P = P_{0} e^{kx} \]
Examples of Exponential Growth
Exponential Growth can be observed in several different professions. From biology to finance, we can see several examples of exponential Growth. Here are some examples of how exponential Growth is applied in everyday life.
Growing Microorganisms in a Culture
A pathologist uses the notion of exponential Growth to expand the microorganism taken from the sample during a pathology test in the hospital. Microbes proliferate quickly when given infinite resources and an appropriate environment. It facilitates the study of the organism in question, making the disease/disorder more straightforward to discover.
Food Being Spoiled
When we leave cooked or uncooked food at room or warm temperature for an extended period of time, it begins to rot. Almost everyone has seen the green discoloration that destroys food and spreads quickly. Microorganisms require a warm environment to multiply and divide at an exponential rate.
The Human Population
The human population is growing at an exponential rate. As of February 2019, the world’s population had surpassed 7.71 billion, and the figure is increasing by the day. However, development is slowing in specific locations, or the population is declining. China has the most people, with India coming in second. However, it is expected that India will lead the globe by 2030.
Compound Interest
Compound interest is adding interest to the principal amount of a loan or deposit or interest on interest in layman’s terms. Compound interest at a constant interest rate provides capital with exponential Growth.
Pandemics
A pandemic is the spread of a disease across a large geographic area. For example, during the COVID-19 pandemic in 2020, the number of patients infected with the virus surged, indicating an exponential growth of the disease.
Invasive Species
Most of us have probably heard of the Water Hyacinth, the worst invasive weed in the world. They are typically planted for aesthetic reasons. They frequently clog rivers due to their exponential development, preventing the water’s creatures from receiving sunlight and oxygen. A non-native species that spreads to an extent thought to harm the environment, the economy, or human health is considered invasive.
Fire
Most of us have witnessed forests burn to the ground in hours. It has been discovered that a fire’s damage area and burning time are related exponentially.
Cancer-Causing Cells
One of the worst diseases in the world is cancer. Cancer has already claimed the lives of millions of people, and millions more are currently battling the disease. To make matters worse, if left untreated, cancer cells multiply exponentially.
Solved Examples
The Exponential Growth Calculator provides you with the exponential growth equation quickly after you give the necessary information.
Here are some examples solved using the Exponential Growth Calculator:
Example 1
While conducting his research, a mathematician comes across the following values:
\[ y = 3+xx^{2} \]
The mathematician needs to find the exponential Growth of the given equation. Using the Exponential Growth Calculator, find the exponential Growth of the equation.
Solution
Using the Exponential Growth Calculator, we can easily solve the equation. First, we enter the left side of the equation into the Exponential Growth Calculator; the left side of the equation is y. After entering the left-hand side of the equation, we enter the “a” value in the calculator; the “a” value is 3 + x. Once the “a” value is inputted into the calculator, we add the “b” value of the equation; the “b” value is x. Now we enter the final value power value, x, into the Exponential Growth Calculator; the value of x is 2.
Finally, after entering all the values in the calculator, we click the “Submit” button. The Exponential Growth Calculator provides the results in a separate window. The results are shown instantly.
The following results are generated from the Exponential Growth Calculator:
Input:
\[ y = 3+xx^{2} \]
Result:
\[ y = 3+x^{3} \]
Plot:
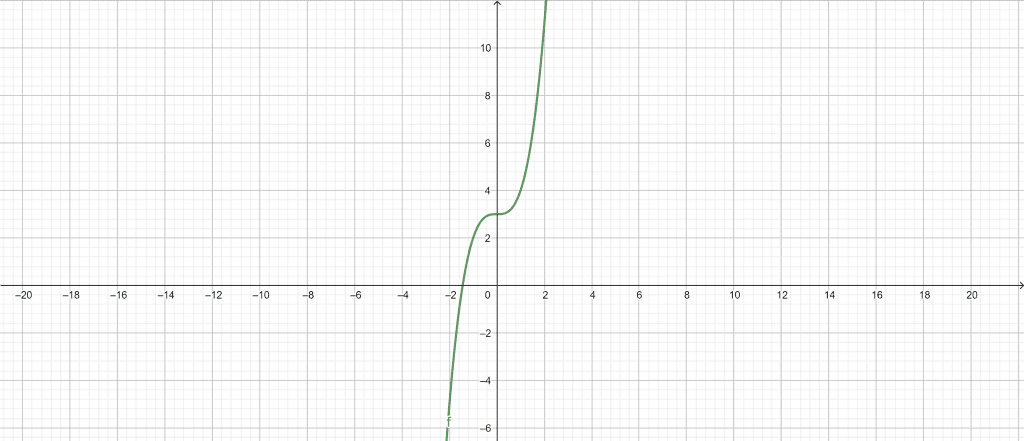
Figure 1
Alternate Forms:
\[ -x + y -3 = 0 \]
Real Roots:
\[ x = -\sqrt[3]{3} \]
Complex Roots:
\[ x = \frac{-\sqrt[3]{3}}{2} + \frac{1}{2} \imath{3^{\frac{3}{5}}} \]
\[ x = \frac{-\sqrt[3]{3}}{2} – \frac{1}{2} \imath{3^{\frac{3}{5}}} \]
Domain:
\[ \mathbb{R} \]
Range:
\[ \mathbb{R} \]
Partial Derivative:
\[ \frac{\partial }{\partial x}(x^{3} + 3) = 3x^{2} \]
\[ \frac{\partial }{\partial y}(x^{3} + 3) = 0 \]
Implicit Derivative:
\[ \frac{\partial x (y) }{\partial y} = \frac{1}{3x^{2}} \]
\[ \frac{\partial y (x) }{\partial x} = 3x^{2} \]
Example 2
A high school student is given the following equation:
\[ y = 3x + 4x^{3} \]
Using the Exponential Growth Calculator, find the exponential equation of the given equation.
Solution
We may simply calculate the equation using the Exponential Growth Calculator. First, we enter the equation’s left half, y, into the Exponential Growth Calculator. We enter the “a” number in the calculator after entering the left-hand side of the equation; the “a” value is 3x + 1. After entering the “a” value into the calculator, we add the equation’s “b” value, 4x. Now we enter the final power value, x, into the Exponential Growth Calculator; x equals 3.
Finally, we click the “Submit” button after inputting all values into the calculator. The findings of the Exponential Growth Calculator are displayed in a different window. The findings are displayed immediately.
The following results are extracted from the Exponential Growth Calculator:
Input:
\[ y = 3x + 4x^{3} \]
Plots:
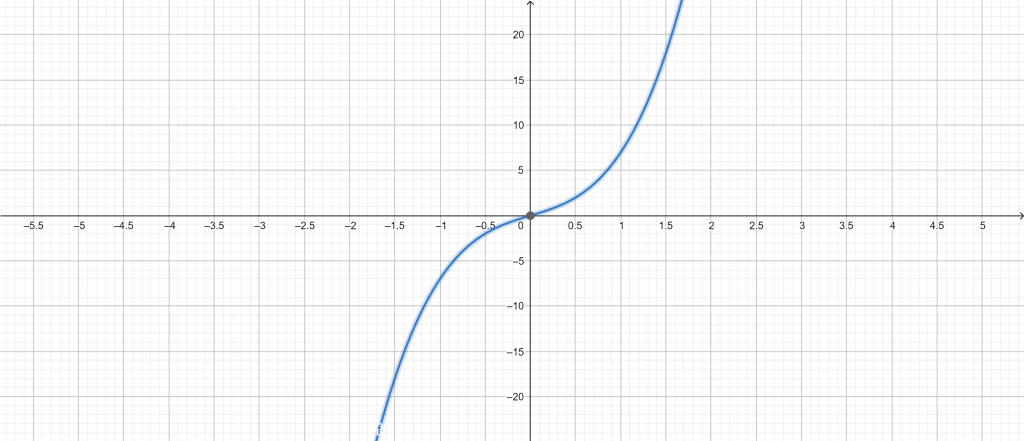
Figure 2
Alternate Forms:
\[ y = x(4x^{2} + 3) \]
\[ -4x^{3} – 3x + y = 0 \]
Real Roots:
x = 0
Complex Roots:
\[ x = – \frac{i \sqrt{3}}{2} \]
\[ x = \frac{i \sqrt{3}}{2} \]
Domain:
\[ \mathbb{R} \]
Range:
\[ \mathbb{R} \]
Partial Derivative:
\[ \frac{\partial }{\partial x}(4x^{3} + 3x) = 12x^{2} + 3 \]
\[ \frac{\partial }{\partial y}(4x^{3} + 3x) = 0 \]
Example 3
Consider the following equation:
\[ y = 5x^{2} \]
Use the Exponential Growth Calculator to find the exponential Growth.
Solution
We could just use the exponential growth calculator to solve the equation. The Exponential Growth Calculator takes the equation’s left half, y. Having entered the left side of the equation, we now enter the “a” number, 5. We add the equation’s “b” value, x, after inputting the “a” value in the calculator. x = 2 is the power value we enter into the Exponential Growth Calculator.
We enter all the values into the calculator and click “Submit.” In a separate window, the Exponential Growth Calculator’s results are shown. The results are presented right away.
Results from the Exponential Growth Calculator can be seen below:
Input:
\[ 5x^{2} \]
Geometric Figure:
Parabola
Plot:
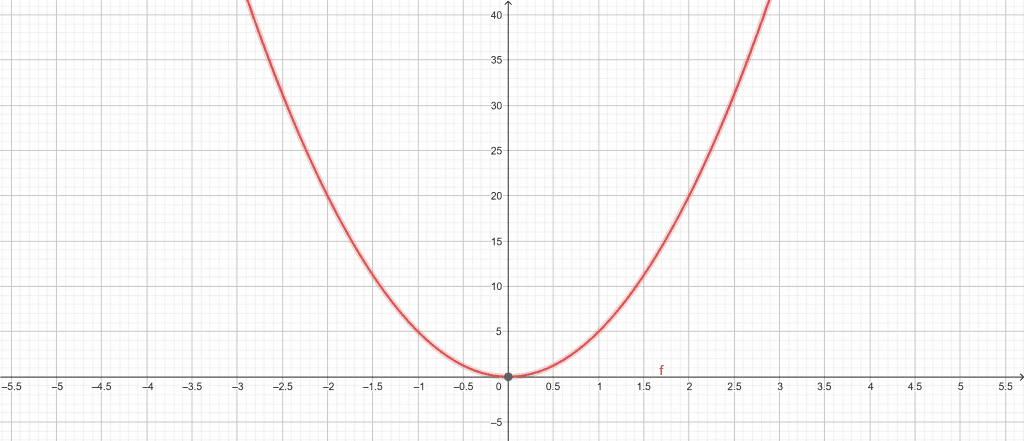
Figure 3
Alternate Forms:
\[ y – 5x^{2} \]
Roots:
x = 0
Domain:
\[ \mathbb{R} \]
Partial Derivative:
\[ \frac{\partial }{\partial x}(5x^{2}) = 10x \]
\[ \frac{\partial }{\partial y}(5x^{2}) = 0 \]
All images/graphs were made using GeoGebra.
