JUMP TO TOPIC
Law of Exponents Calculator + Online Solver With Free Steps
The Laws of Exponents Calculator is a helpful tool that finds the result of an input expression by using basic rules of exponents. The calculator’s input is the expression having various terms with bases and exponents.
The calculator simply returns the resultant number obtained by solving the given expression. It can handle any kind of problem, from the simplest to complex ones.

What Is a Laws of Exponents Calculator?
A Laws of Exponents Calculator is an online tool which can solve your exponents-related mathematical problems.
Numbers with exponents are frequently observed in fields of science and mathematics. Most solutions to real-life problems use exponent laws. For instance, using prefixes in physics to perform basic operations on large values.
Similarly, measurement units to represent quantities are in the form of exponents. Like determining the area in square feet or volume in cubic meters. That’s why we need such a tool that can fastly solve these problems
Thus, you can use the Laws of Exponents Calculator to obtain perfect solutions for your mathematical problems. This simple calculator is accessible to everyone, wherever, at any time.
In the coming sections, you can find more information on the workings of this calculator and how to use it.
How To Use the Laws of Exponents Calculator?
To use the Laws of Exponents Calculator, you need to simply enter your mathematical expression in the input box and click a button and you will be presented with the results.
Once you have a valid expression, you only have to perform two simple steps to use this calculator. The steps are given below:
Step 1
First, enter the expression you want to solve in the Simplify box. The expression should have terms that have a base and their exponents and should have operations between them if multiple terms are there. For instance, it can be an expression like $x^{a}$ x $y^{b}$.
Step 2
Then click on the Submit button to get the solution. The solution will be an answer to the given expression obtained using the exponent’s laws.
How Does the Laws of Exponents Calculator Work?
The Laws of Exponents Calculator works by taking the input expression and applying the appropriate law of exponent to find the answer to this expression.
The working of this calculator is based on fundamental laws of exponents, so we need to discuss the exponents and their laws to further understand the operation of this calculator.
What Are the Exponents?
Exponents are the values written in the power of a number. This describes how many times this number should multiply by itself. This number being multiplied is called the base. These numbers can be represented as $x^{n}$.
For example, a base y is raised to the power 3, then the expression to solve this number is as follows.
$y^{3}$ = y x y x y
To simplify the expression having such terms, there are seven basic laws often used. Let’s discuss them one by one briefly.
Product Law
The product law of exponent states that two terms are multiplied with identical bases and different powers then add both powers. For instance, if $x^{a}$ is being multiplied with $x^{b}$ then the result of multiplication can be written as:
\[ x^{a} \times x^{b} = x^{a+b} \]
This needs to be noted if the bases are also different then each of the terms is solved separately and multiplied.
Quotient Law
The quotient law of exponents says that if two expressions with the same bases and different exponents are divided, then subtract both exponents. Let’s say an expression $y^{c}$ is divided by another expression which is $y^{d}$ then it can be represented as:
\[ \frac{x^{a}}{x^{b}} = x^{a-b} \]
Here the exponent in the denominator is always subtracted from the exponent in the numerator.
Power of a Power
This law states that if the power in a term is raised to another power, then simply multiply both powers. For example, the power a in term $z^{}$ is raised to another power let’s suppose b, then it can be expressed as:
\[ z^{a^{b}} = z^{a x b} \]
Power of Product
According to the power of product law, if the base is a product of two numbers then the result can be obtained by distributing the exponent to each of the numbers in the base separately. See the below expression to further clarify this concept.
\[ (xy)^{b} = x^{b} \cdot y^{b} \]
Power of Quotient
If the base is in the form of a fraction of two numbers, then assign the power to the numerator and denominator of the base individually. This is known as the Power of Quotient Law.
Let’s take an example to understand it, an expression $\frac{y}{z}$ has a single power which is c. Then it can be written as:
\[ (\frac{y}{z})^{c} = \frac{ y^{c} }{ z^{c} } \]
Negative Exponent Law
The negative exponent law states that if a base has a negative exponent then to make it positive write this expression in the denominator of a fraction with the numerator equal to 1. For instance, the term $x^{- d}$ can be expressed as:
\[ x^{- d}= \frac{1}{ x^{d} } \]
Zero Exponent Law
This law simply states that if any base has power equal to zero, then the result of such expression is 1. This can be written as:
$z^{0}$ = 1
No matter what number the z is, if the exponent is zero, it will be equal to one always.
Solved Examples
There are some examples solved by the Laws of Exponents Calculator. Each example is explained in detail.
Example 1
Simplify the following mathematical expression using the laws of the exponents.
\[ 3^{8} x 3^{3} \]
Solution
This expression simplified by this calculator is given below. It performs the addition of both exponents and multiplies the base the resultant sum times by itself that is product law.
\[ 3^{8} x 3^{3} = 3^{11} = 177147 \]
Example 2
A student in a maths exam is given the below expression:
\[ \frac{12x^{4}}{4x^{2}} \]
He is asked to simplify the expression and find the answer to the expression.
Solution
The expression is a fraction with terms that have a constant number multiplied by a variable with some exponent. The constants are treated separately whereas the variable is the same, so the quotient law is applied to the variable part.
\[ \frac{12x^{4}}{4x^{2}} = 3x^{2} \]
As the expression involves variables, so it plots the simplified expression in the x-y plane. The plot can be seen in figure 1.
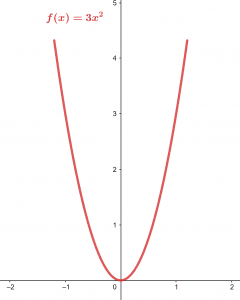
Figure 1
All the Mathematical Images/Graphs are created using GeoGebra.
