JUMP TO TOPIC
Square Root Property Calculator + Online Solver With Free Steps
The online Square Root Property Calculator is a tool that solves equations having variables in the form of squares. The calculator takes these square equations as the input.
As the variable has a square, so the variable can have a maximum of two values. The calculator solves the given equation to find these two values of the unknown variable in the equation.

What Is a Square Root Property Calculator?
A Square Root Property Calculator is an online calculator that uses square root property to determine the values of the unknown variables in equations.
Equations with variables having squares are often called quadratic equations because the highest degree in such equations is also two. The quadratic equations have a shape like a parabola in the cartesian plane.
These equations have deep roots in the research areas of physics and geometry. They are used in many real-life problems like optimization of functions, objects having projectile motion, and calculation of quantities like surface area.
Also, the general form of many geometric shapes involves squares such as circles, parabolas, ellipses, etc. There are multiple methods to solve equations with squares but you can simply use the property of square root to find their solution.
This superb calculator uses the same property to solve the square variable equations and provide you with the most feasible solutions. This calculator is one of the best online tools available because of its simplicity and friendly interface.
There is no need for any specific device to use it. Anyone with access to a good internet connection can use this calculator in the browser available on their device.
How To Use the Square Root Property Calculator?
You can use the Square Root Property Calculator by inserting your mathematical equations one by one in the given input box. All you need to do is to insert the values, click on the button, and the answer will be presented to you in a couple of moments.
You need an equation that has a perfect square on one side and a constant number on the other side. This constant may or may not be a perfect square. Once you have the proper equation, now you can play with this tool.
To get the best results from this calculator, you may follow the detailed step-by-step procedure given below:
Step 1
Enter the mathematical equation in the box with the name Enter the Equation. Enter the perfect square on the right side and the constant number on the left side of the equation.
Step 2
Press the Solve button to get the final solution.
Result
The solution consists of three parts. The first part is the interpretation of the given equation by the calculator. Then the second part gives the values for two roots of the unknown variable.
Finally, the third part graphs the mathematical equation in the cartesian plane. The graph notifies about the location of roots by highlighting them as separate points and draws a line that passes through both points.
How Does the Square Root Property Calculator Work?
This calculator works by solving the given quadratic equation using the square root property. This property applies the square root on the perfect square term involving the required variable in the quadratic equations.
The square root property is mainly used when there is a perfect square of a variable. One should know about this property when there is a requirement to solve quadratic equations.
Square Root Property
The square root property is used to find the integer that, when multiplied by itself, results in a perfect square.
The formal definition of this property says “If there is a variable x and a non-zero number m, then the quadratic equation $x^2=m$ has exactly two solutions given by $x=\sqrt{m}$ and $x=-\sqrt{m}$.”
What Is the Perfect Square?
A Perfect Square is a positive integer that is obtained by multiplying the integer itself or by taking the second power of that integer. It is represented by $x^2$ where x can be an integer or a variable if there is a perfect square term that involves a variable.
Properties of Roots
Mathematical Roots have some following properties depending on the operation they are used for. The square root also has the same properties.
Multiplicative Property
This property states that if there are two or more numbers with identical radicands, then all the numbers can be multiplied together for simplification. For instance, if there are two expressions $a\sqrt{x}$ and $b\sqrt{x}$, then they can be simplified as:
\[a\sqrt{x}*b\sqrt{x}=a*b\sqrt{x}\]
Quotient Property
It states that the square root of a fraction is equal to the square root of its numerator and its denominator. In general, this property allows writing $\sqrt{\frac{x}{y}}$ as $\sqrt{x}/\sqrt{y}$.
Equality Property
This property allows applying the same operation on both sides of the equation to find the value of the required variable.
If there is a perfect square on both sides of the equation then by taking the square root on both sides, the value of the variable can be found.
Solving Quadratic Equations Using Square Root Property
The square root property is used to solve the quadratic equations that are not solvable through factorization. In this method, the quadratic term is isolated on one side of the equation, then the square root is taken on both sides of the equation.
Afterward, simplify the equation to get the value of the variable. Since it is a quadratic equation, it has two solutions, one with a + sign and the other with a – sign.
This property can be used on those equations that have only a quadratic term and a constant term but no linear term (b=0).
Solved Examples
Here are some solved examples for a better understanding of this calculator.
Example 1
Solve the following quadratic equation:
\[5x^2=15\]
Solution
The above equation can easily be solved by inserting it into the square root property calculator. The value of x is given by:
\[x= \pm\sqrt {3}\]
Root Plot
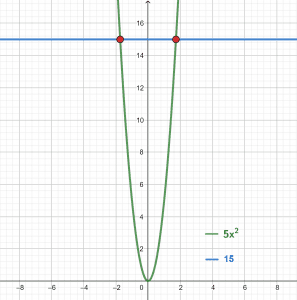
Figure 1
Example 2
Consider the following equation:
\[2(x-2)^2=5\]
Find the value of x.
Solution
The value of $x$ can be found by using the square root property calculator.
\[x=2 \pm \sqrt{\frac{5}{2}}\]
Root Plot
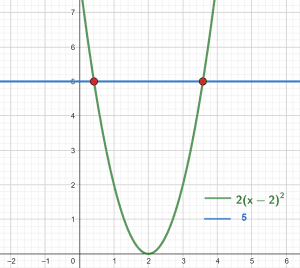
Figure 2
All the Mathematical Images/Graphs are created using GeoGebra.
