JUMP TO TOPIC
Length of Polar Curve Calculator + Online Solver With Free Steps
The Length of Polar Curve Calculator is an online tool to find the arc length of the polar curves in the Polar Coordinate system.
A polar curve is a shape obtained by joining a set of polar points with different distances and angles from the origin. This set of the polar points is defined by the polar function.
The result displays the exact value of length and polar plot for the input function.

What Is a Length of Polar Curve Calculator?
A Length of Polar Curve Calculator is an online calculator that can be used to determine the arc length of polar function over a specified interval.
The arc length is a measure of distance between two points along a segment of the polar curve. This simple calculator computes the arc length by quickly solving the standard integration formula defined for evaluating the arc length.
The formula for arc length of polar curve is shown below:
\[ Length = \int_{\theta=a}^{b} \sqrt{r^2 + (\dfrac{dr}{d\theta})^2} d\theta \]
Where the radius equation (r) is a function of the angle ($\theta$). The integral limits are the upper and lower limit of angle. The function is differentiated concerning the angle which is denoted by $dr/d\theta$.
Therefore, finding out the length needs several steps to be done, which is a time-intensive procedure and there is a chance of mistakes if solved by hand. But you can save your precious time by using this superb tool that provides you with the most accurate results.
This online calculator is readily available in your browser at any time and place. You don’t need any prior knowledge or require any skill to operate this calculator.
How To Use the Length of Polar Curve Calculator?
You can use the Length of Polar Curve Calculator by inserting the values of the input components in their mentioned fields. Follow the given steps to get good results.
Step 1
Enter the polar equation which is a function of angle ($\theta$) in the Polar Equation R tab. It can be any algebraic or trigonometric equation.
Step 2
Enter the starting point of the angle in the box named From and the endpoint in the To box. The points can be any value between 0 and $2\pi$.
Step 3
Press the Submit button to get the desired result.
Result
The final result is provided in two steps. The first part is the length of the polar curve between the points you specified and the second part is the polar graph that is drawn within that particular span.
The polar graph displays the total polar curve in the dotted lines, whereas the specific portion of the curve for which arc length is evaluated is shown in a straight line.
Solved Examples
To further clarify the use of the calculator, let’s explore some solved examples from this handy calculator.
Example 1
Consider the following polar equation:
r($\theta$) = 6sin($\theta$)
The interval of angle for calculating the arc length is given as:
\[ \theta = (0,\pi/2) \]
Solution
The calculator gives the following results.
Length of Polar Curve:
\[ \int_{0}^{\pi/2} 6 d\theta = 3\pi \approx 9.4248 \]
Polar Plot:
The polar plot is depicted in Figure 1. The straight bold line represents the section of the curve for which arc length is calculated while the dotted line shows the remaining portion of the curve.
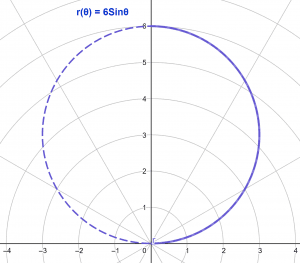
Figure 1
Example 2
Consider the below-mentioned radius equation:
r($\theta$) = 5+cos(4$\theta$)
The integral limits for angle are as follows:
$\theta$ = (0,$\pi$)
Solution
For the above polar function, our calculator attains the following arc length and polar plot.
Length of Polar Curve:
\[ \int_{0}^{\pi} \sqrt{ (5+\cos(4\theta))^2 + \sin^{2} (4\theta) } d\theta \approx 17.9971 \]
Polar Plot:
The polar plot is shown in Figure 2 below:
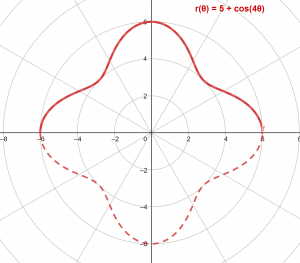
Figure 2
All the Mathematical Images/Graphs are created using GeoGebra.
