JUMP TO TOPIC
Line Equation From Two Points Calculator + Online Solver With Free Steps
The Line Equation From Two Points Calculator computes the equation of a line from the two points on the line in the x-y plane.
The two points are represented as ( x1, y1) and (x2, y2). The user must enter the x-y coordinates of both the points for the calculator to find the equation of the line.
The equation of a line is represented by the mathematical formula:
y = mx + b
Where m is the slope of the line and b is the y-intercept.
The slope m of a line is the measure of the steepness of a line and also defines the direction of the line. It describes the change in the y coordinates for the x coordinates of the points in a line.
The formula for the slope of a line is given by
\[ m = \frac{ y_2 \ – \ y_1 }{ x_2 \ – \ x_1 } \]
A negative slope means that the line is moving in the downward direction and a positive slope means that the line is going upwards.
The y-intercept b in the line equation is the y-coordinate when the x-coordinate is equal to zero that is the point ( 0,b ). The line cuts the y-axis at the y-intercept in the equation.
The calculator also shows the line in a 2-D graph with x and y axis. It also calculates the x-intercept and the y-intercept from the line equation.

What Is a Line Equation With Two Points Calculator?
The Line Equation From Two Points Calculator is an online tool that is used to calculate the equation, slope, x-intercept, and y-intercept of a line, taking two points on the line as input. It also plots the line in a x-y plane.
A line is formed from an infinite set of points having x and y coordinates. So, the line equation is a function of y to x.
The slope, x-intercept, and y-intercept remain unchanged throughout the line.
How To Use the Line Equation With Two Points Calculator
The user can use the Line Equation From Two Points Calculator by following the steps given below.
Step 1
The user must enter the first point of the line whose equation is required in the calculator’s input tab. The point is (x1, y1) which passes through the line.
The values of x1 and y1 should be entered by the user in the block labeled, “Find the equation of line passes through the point”. The point should lie in the x-y plane.
For the default example, the first point which passes through the line is ( 1,3 ).
Step 2
The user must now enter the second point in the input window of the calculator. The point is represented by (x2, y2) which also passes through the line. It should be entered in the block against the title, “and the point”.
The second point of the line is ( -1,5 ) for the default example.
Step 3
The user must now press the button “Submit” for the calculator to process the two points (x1, y1) and (x2, y2) of a line. The calculator computes the output and displays the result in another window.
Output
The Output displayed by the calculator consists of the four windows given below.
Input Interpretation
The calculator interprets the input and displays the two points entered by the user in this window. The Cartesian equation is an equation consisting of Cartesian or x-y coordinates.
The Input Interpretation for the default example is displayed as follows:
Line points = ( 1,3 ) , ( – 1,5 ) = Cartesian Equation
Result
The calculator computes the line equation and displays the result in this window. The line equation used is the slope-intercept form which is given below:
y = mx + b
First, the calculator computes the slope m and the y-intercept b and places the values in this equation to get the line equation.
The calculator also provides all the mathematical steps by pressing on “Need a step-by-step solution to this problem”.
For the default example, the input points are ( 1,3 ) and ( -1,5 ). The slope for these set of points is calculated as follows:
\[ m = \frac{ y_2 \ – \ y_1 }{ x_2 \ – \ x_1 } \]
Here, (x1 = 1, y1 = 3) and (x2 = -1 , y2 = 5). Putting the values in the slope equation gives:
\[ m = \frac{ 5 \ – \ 3 }{ – \ 1 \ – \ 1 } \]
\[ m = \frac{ 2 }{ – \ 2 } \]
m = – 1
Thus, the slope of the line is -1.
Putting the value of m in the line equation gives:
y = – x + b
The y-intercept b is calculated by putting any given point in the line equation. Putting the point ( 1,3 ) in the above equation gives:
3 = – 1 + b
b = 4
So, the slope-intercept form of the line equation given by the calculator is:
y = 4 – x
Visual Representation
The calculator also shows the plot of the line equation in this window. The line shown lies in the x-y plane. The user can visualize the y-intercept of the line as it cuts the y-axis.
For the default example, the graph for the line equation {y = 4 – x} is shown in figure 1.
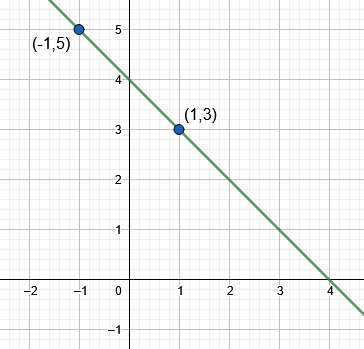
Figure 1
Properties of Line
The properties of the line include the x-intercept, y-intercept, and the slope.
The calculator computes the x-intercept by putting the value of y = 0 and the y-intercept b in the line equation.
For the default example, the equation is:
y = – x + b
Putting y = 0 and b = 4 in the above equation gives:
0 = – x + 4
x = 4
The calculator displays the slope, x-intercept, and y-intercept for the default example as follows:
x-intercept = 4
y-intercept = 4
slope = – 1
Solved Example
The following example is solved through the Line Equation From Two Points Calculator.
Example 1
Calculate the slope, x-intercept, y-intercept, and the slope-intercept form of the line equation passing through the points ( -4,1 ) and ( 0,-7 ).
Solution
The user must first enter the two points in the calculator’s input window as specified in the example. After submitting the points, the calculator computes the line equation and displays the output.
The Input Interpretation shown by the calculator is:
Line points = ( – 4,1 ) , ( 0,- 7 ) = Cartesian Equation
The calculator shows the slope-intercept form of the line equation in the Result window as follows:
y = – 2x – 7
From the equation, the slope m is -2 and the y-intercept b is -7.
The Visual Representation shows the graph for the above equation as shown in figure 2.
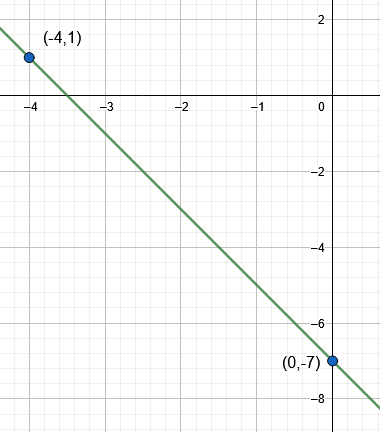
Figure 2
The graph shows a line passing through the two points ( -4,1 ) and ( 0,-7 ).
The calculator also displays the properties of the line equation as follows:
\[ x-intercept = \frac{- \ 7}{2} = – \ 3.5 \]
y-intercept = – 7
slope = – 2
All the images are created using Geogebra.
