JUMP TO TOPIC
Radical Equation Calculator + Online Solver With Free Steps
The Radical Equation Calculator solves a given radical equation for its roots and plots it. A radical equation is one with variables under the radical sign “$\surd\,$” as in:
\[ \text{radical equation} : \sqrt[n]{\text{variable terms}} + \text{other terms} = 0 \]
\[ \sqrt{5x^2+10x}+4x-7 = 0 \]
The calculator supports multi-variable equations, but the intended usage is for single-variable ones. That is because the calculator accepts only one equation at a time and cannot solve systems of simultaneous equations where we have n equations with m unknowns.
Thus, for multi-variable equations, the calculator outputs roots in terms of the other variables.

What Is the Radical Equation Calculator?
The Radical Equation Calculator is an online tool that evaluates the roots for a given radical equation representing a polynomial of any degree and plots the results.
The calculator interface consists of a single text box labeled “Equation.” It is self-explanatory – you enter the radical equation to solve here. You may use any number of variables, but, as mentioned earlier, the intended usage is for single-variable polynomials of any degree.
How To Use the Radical Equation Calculator?
You can use the Radical Equation Calculator by entering the given radical equation into the input text box. For example, suppose you want to solve the equation:
\[ 7x^5 +\sqrt{6x^3 + 3x^2}-2x-4 = 0 \]
Then you can use the calculator by following the step-by-step guidelines below.
Step 1
Enter the equation in the text box. Enclose the radical term in “sqrt(radical term)” without quotes. In the example above, you would enter “7x^5+sqrt(6x^3+3x^2)-2x-4=0” without quotes.
Note: Do not enter just the side of the equation with the polynomial! Otherwise, the results will not contain the roots.
Step 2
Press the Submit button to get the results.
Results
The result section primarily consists of:
- Input: The calculator’s interpretation of the input equation. Useful for verifying the equation and ensuring that the calculator handles it correctly.
- Root Plots: 2D/3D plots with the roots highlighted. If at least one of the roots is complex, the calculator additionally draws them on the complex plane.
- Roots/Solution: These are the exact values of the roots. If they are a mixture of complex and real values, the calculator shows them in the separate sections “Real Solutions” and “Complex Solutions.”
There are also a couple of secondary sections (possibly more for different inputs):
- Number Line: The real roots as they fall onto the number line.
- Alternate Forms: Various rearrangements of the input equation.
For the example equation, the calculator finds a mixture of real and complex roots:
\[ x_{r} \approx 0.858578 \]
\[ x_{c_1,\,c_2} \approx 0.12875 \pm 0.94078i \qquad x_{c_3,\,c_4} \approx -0.62771 \pm 0.41092i \]
How Does the Radical Equation Calculator Work?
The Radical Equation Calculator works by isolating the radical term on one side of the equation and squaring both sides to remove the radical sign. After that, it brings all the variable and constant terms to one side of the equation, keeping 0 on the other end. Finally, it solves for the roots of the equation, which is now a standard polynomial of some degree d.
Higher-order Polynomials
The calculator can quickly solve for polynomials with degrees greater than four. That is significant because there is no general formulation for solving d-degree polynomials with d > 4.
Extracting the roots of these higher-order polynomials requires a more advanced method such as the iterative Newton method. By hand, this method takes a long time because it is iterative, requires initial guesses, and may fail to converge for certain functions/guesses. However, this is not a problem for the calculator!
Solved Examples
We will stick to lower-order polynomials in the following examples to explain the basic concept since solving higher-order polynomials with the Newton method will take a lot of time and space.
Example 1
Consider the following equation:
\[ 11 + \sqrt{x-5} = 5 \]
Calculate the roots if possible. If not possible, explain why.
Solution
Isolating the radical term:
\[ \begin{aligned} \sqrt{x-5} &= 5-11 \\ &= -6 \end{aligned} \]
Since the square root of a number cannot be negative, we can see that no solution exists for this equation. The calculator verifies this as well.
Example 2
Solve the following equation for y in terms of x.
\[ \sqrt{5x+3y}-3 = 0 \]
Solution
Isolating the radicals:
\[ \sqrt{5x+3y} = 3 \]
Since this is a positive number, we are safe to proceed. Squaring both sides of the equation:
\[ 5x+3y = 3^2 = 9 \]
Rearranging all terms to one side:
5x+3y-9 = 0
It is the equation of a line! Solving for y:
3y = -5x+9
Dividing both sides by 3:
\[ y = -\frac{5}{3}x + 3 \]
The y-intercept of this line is at 3. Let us verify this on a graph:
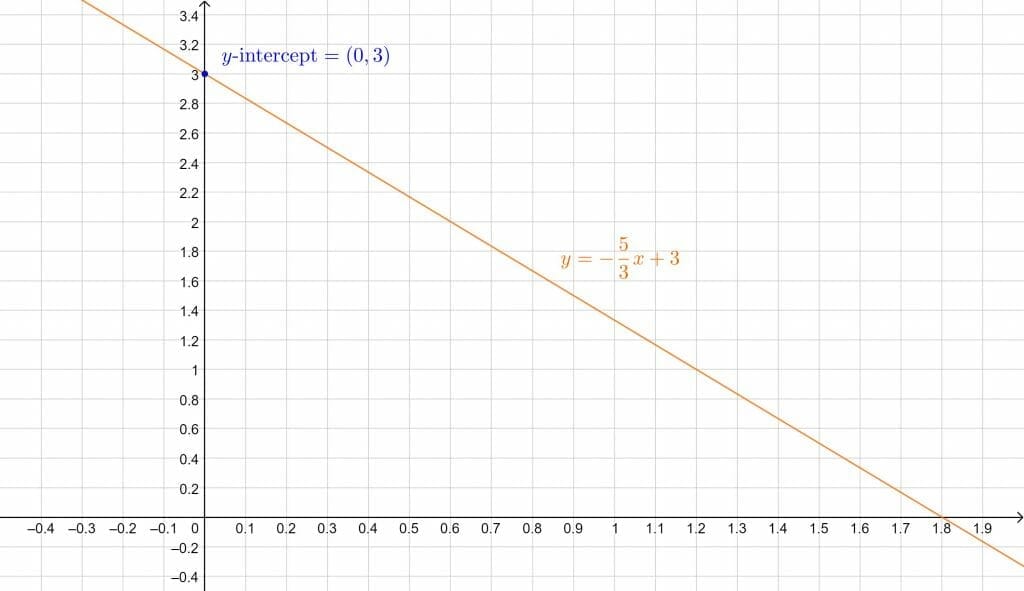
Figure 1
The calculator also provides these results. Note that as we had only one equation, the solution is not a single point. It is constrained to a line instead. Similarly, if we had three variables instead, the set of possible solutions would lie on a plane!
Example 3
Find the roots for the following equation:
\[ \sqrt{10x^2+20x}-3 = 0 \]
Solution
Separating the radical term and squaring both sides after:
\[ \sqrt{10x^2 + 20x} = 3 \]
\[ 10x^2 + 20x = 9 \, \Rightarrow \, 10x^2+20x-9 = 0 \]
That is a quadratic equation in x. Using the quadratic formula with a = 10, b = 20, and c = -9:
\begin{align*} x_1,\, x_2 & = \frac{-b \pm \sqrt{b^2-4ac}}{2a} \\\\ & = \frac{-20 \pm \sqrt{20^2-4(10)(-9)}}{2(10)} \\\\ & = \frac{-20 \pm \sqrt{400+360}}{20} \\\\ & = \frac{-20 \pm \sqrt{760}}{20} \\\\ & = \frac{-20 \pm 27.5681}{20} \\\\ & = -1 \pm 1.3784 \end{align*}
We get the roots:
\[ \therefore , x_1 = 0.3784 \quad , \quad x_2 = -2.3784 \]
The calculator outputs the roots in their exact form:
\[ x_1 = -1 + \sqrt{\frac{19}{10}} \approx 0.3784 \quad,\quad x_2 = -1-\sqrt{\frac{19}{10}} \approx -2.3784 \]
The plot is below:
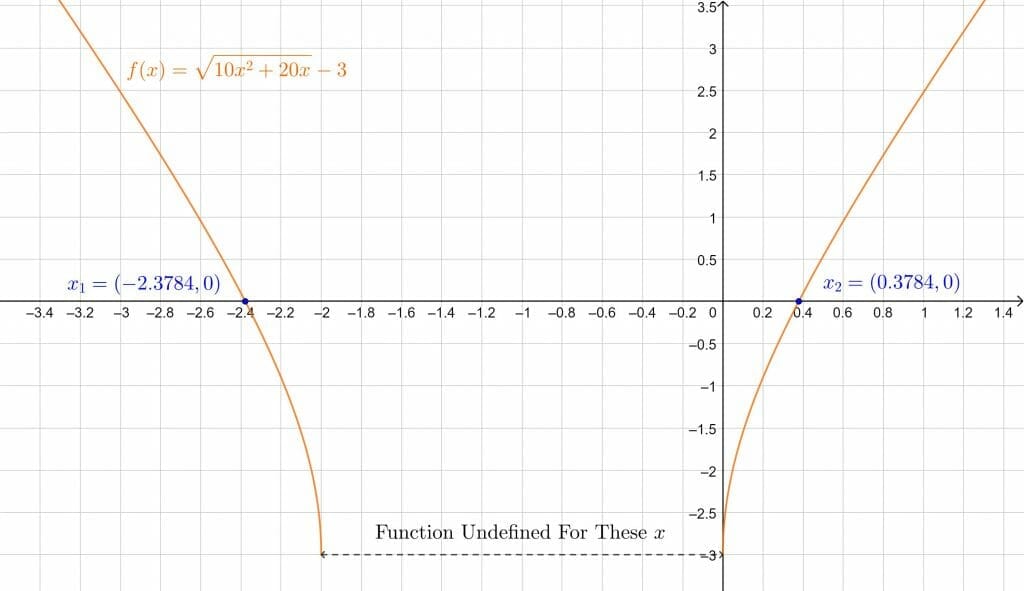
Figure 2
Example 4
Consider the following radical with nested square roots:
\[ \sqrt{\sqrt{x^2-4x}-9x}-6 = 0 \]
Evaluate its roots.
Solution
First, we isolate the outer radical as usual:
\[ \sqrt{\sqrt{x^2-4x}-9x} = 6 \]
Squaring both sides:
\[ \sqrt{x^2-4x}-9x = 36 \]
Now we need to remove the second radical sign as well, so we isolate the radical term again:
\[ \sqrt{x^2-4x} = 9x+36 \]
\[ x^2-4x = 81x^2+648x+1296 \]
\[ 80x^2+652x+1296 = 0 \]
Dividing both sides by 4:
\[ 20x^2+163x+324 = 0 \]
Solving using the quadratic formula with a = 20, b = 163, c = 324:
\begin{align*} x_1,\, x_2 & = \frac{-163 \pm \sqrt{163^2-4(20)(324)}}{2(20)} \\\\ & = \frac{-163 \pm \sqrt{26569 – 25920}}{40} \\\\ &= \frac{-163 \pm \sqrt{649}}{40} \\\\ & = \frac{-163 \pm 25.4755}{40} \\\\ & = -4.075 \pm 0.63689 \end{align*}
\[ \therefore \,\,\, x_1 = -3.4381 \quad , \quad x_2 = -4.7119 \]
However, if we plug in $x_2$ = -4.7119 into our original equation, the two sides are not equal:
\[ 6.9867-6 \neq 0 \]
Whereas with $x_1$ = -3.4381, we get:
\[ 6.04-6 \approx 0 \]
The slight error is due to the decimal approximation. We can verify this in the figure as well:
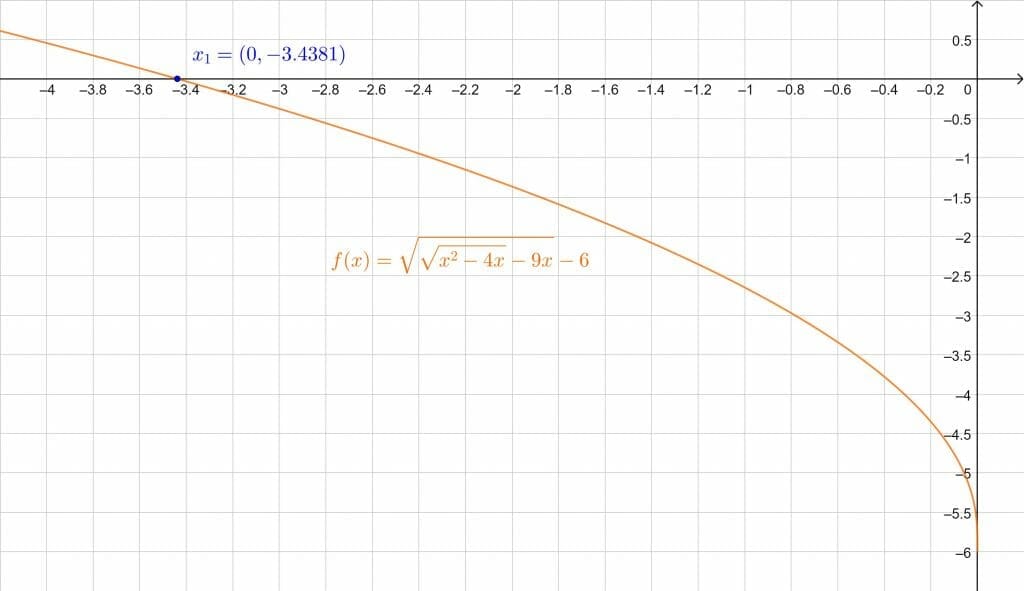
Figure 3
All graphs/images were created with GeoGebra.
