JUMP TO TOPIC
Root Calculator + Online Solver With Free Steps
The Root Calculator finds the square super-root of a given number, variable(s), or some mathematical expression. The square super-root (denoted as ssrt(x), ssqrt(x), or $\sqrt{x}_s$) is a relatively rare mathematical function.
ssrt(x) represents the inverse operation of tetration (repeated exponentiation), and its calculation involves the Lambert W function or the iterative approach of the Newton-Raphson method. The calculator uses the former method and supports multi-variable expressions.

What Is the Root Calculator?
The Root Calculator is an online tool that evaluates the square super-root of some input expression. The input value can contain multiple variable terms such as x or y, in which case the function displays a plot of the results over a range of the input values.
The calculator interface consists of a single, descriptive text box labeled “Find the square super-root of,” which is quite self-explanatory – you enter the value or variable term you want to find here, and that is it.
How To Use the Root Calculator?
You can use the Root Calculator by entering the number whose square super-root is required. You may also enter variables. For example, suppose you want to find the square super-root of 27. That is, your problem looks like this:
\[ \text{ssqrt}(27) \,\, \text{or} \,\, \text{ssrt}(27) \,\, \text{or} \,\, \sqrt{27}_s \]
Then you can use the calculator to solve it in just two steps as follows.
Step 1
Enter the value or expression to find the square super-root for into the input text box. In the example, this is 27, so enter “27” without quotes.
Step 2
Press the Submit button to get the results.
Results
The results are expansive, and which sections show depends on the input. The possible ones are:
- Input: The input expression in the standard form for square super-root calculation with the Lambert W function: $e^{ W_0(\ln(x)) }$ where x is the input.
- Result/Decimal Approximation: The square super-root calculation result – could be either a real or complex number. In the case of variable inputs, this section does not show.
- 2D/3D Plots: The 2D or 3D plots of the result over a range of values for variable terms – replaces the “Result” section. It does not appear when there are more than two variables involved, or nor variables at all.
- Number Line: The result’s value as it falls onto the number line – does not show if the result is complex.
- Alternate Forms/Representations: Other possible representations of the square super-root formulation, like the common fraction form: $e^{ W(\ln(x)) } = \frac{\ln(x)}{W(\ln(x))}$ where x is the input.
- Integral Representations: More alternative representations in the form of integrals if possible.
- Continued Fraction: The “continued fraction” of the result in the linear or fraction format. It only appears if the result is a real number.
- Alternate Complex Forms/Polar Form: Exponential Euler, trigonometric, and polar form representations of the result – only shown if the result is a complex number.
- Position in the Complex Plane: A point visualized at the result coordinates on the complex plane – only appears if the result is a complex number.
How Does the Root Calculator Work?
The Root Calculator works by using the following equations:
\[ \text{ssrt}(y) \,\, \text{where} \,\, y = x^x \,\, \vert \,\, x \in +\mathbb{R} \tag*{$(1)$}\]
And its eventual formulation as the exponential of the Lambert W function:
\[ \text{ssrt}(y) = e^{W(\ln y)} = \frac{\ln y}{W(\ln y)} \tag*{$(2)$} \]
Tetration and Square Super-Roots
Tetration is the operation of repeated exponentiation. The $n^{th}$ tetration of a number x is denoted by:
\[ {}^{n}x = x \upuparrows n = x^{x^{\cdot^{\cdot^{\cdot^{x}}}}} \]
It is convenient to assign a subscript to each instance of x as $x_1,\, x_2,\, x_3,\, \ldots,\, x_n = x$:
\[ {}^{n}x = x_1^{x_2^{\cdot^{\cdot^{\cdot^{x_n}}}}} \]
Thus there are n copies of x, repeatedly exponentiated n-1 times. Think of x1 as level 1 (lowest or base), x2 as level 2 (1st exponent), and xn as level n (highest or (n-1)th exponent). Within this context, it is sometimes referred to as a power tower of height n.
The square super-root is the reverse operation of the second tetration $x^x$. That is, if:
\[ y = x^x \iff \text{ssrt}(y) = \sqrt{y}_s = x \]
Solving $y = x^x$ for x (the same process as finding an inverse function) leads to the formulation of the square super-root in equation (2).
Lambert W Function
In equation (2), W represents the Lambert W function. It is also called the Product Logarithm or Omega function. It is the converse relation of $f(w) = we^w = z$ where w, z $\in \mathbb{C}$, and has the property:
\[ we^w = z \iff W_k(z) = w \,\, \text{where} \,\, k \in \mathbb{Z} \]
It is a multi-valued function with k branches. Only two of these are required when dealing with real numbers, namely $W_0$ and $W_{-1}$. $W_0$ is also called the Principal Branch.
Asymptotic Approximation
As tetration involves large values, it is sometimes required to use the asymptotic expansion to estimate the value of the function Wk(x):
\[ \begin{aligned} W_k &= L_1-L_2 + \frac{L_2}{L_1} + \frac{L_2 \!\left(-2+L_2 \right)}{2L_1^2} + \frac{L_2 \!\left( 6-9L_2+2L_2^2 \right)}{6L_1^3} \\ & \quad + \frac{L_2 \!\left(-12+36L_2-22L_2^2+3L_2^3 \right)}{12L_1^4} + \cdots \end{aligned} \tag*{$(3)$} \]
Where:
\[ L_1,\, L_2 = \left\{ \begin{array}{lcl} \ln x,\, \ln (\ln x) & \text{for} & k = 0 \\ \ln(\!-x),\, \ln(\!-\!\ln(\!-x)) & \text{for} & k = -1 \end{array} \right. \]
Number of Solutions
Recall that inverse functions are those that provide a unique, one-to-one solution. The square super-root is not technically an inverse function because it involves the Lambert W function in its calculations, which is a multi-valued function.
Because of this, the square super-root might not have a unique or single solution. Unlike square roots, however, finding the exact number of square super-roots (called the $n^{th}$ roots) is not simple. In general, for ssrt(x), if:
- x > 1 in ssrt(x), there exists one square super-root also greater than 1.
- $e^{-\frac{1}{e}}$ = 0.6922 < x < 1, then there are potentially two square super-roots between 0 and 1.
- 0 < x < $e^{-\frac{1}{e}}$ = 0.6922, the square super-root is complex, and there are infinitely many possible solutions.
Note that in the case of many solutions, the calculator will present one.
Solved Examples
Example 1
Find the square super-root of 256. What is the relationship between the result and 256?
Solution
Let y be the desired result. We then require:
\[ y = \sqrt{256}_s \]
On inspection, we see that this is a simple problem.
\[ \because 4^4 = 256 \, \Rightarrow \, y = 4 \]
No need to compute the long way for this!
Example 2
Evaluate the third tetration of 3. Then, find the result’s square super-root.
Solution
\[ 3^{3^{3}} = 7.6255 \!\times\! 10^{12} \]
Using equation (2), we get:
\[ \sqrt{7.6255 \!\times\! 10^{12}}_s = e^{ W \left( \ln \left(7.6255 \!\times\! 10^{12} \right) \right) } = \frac{\ln \!\left( 7.6255 \!\times\! 10^{12} \right)}{W \!\left( \ln \!\left( 7.6255 \!\times\! 10^{12} \right) \right)} \]
Using the approximation in equation (3) up to three terms, we get:
\[ \sqrt{7.6255 \!\times\! 10^{12}} \approx \mathbf{11.92} \]
Which is close to the calculator’s result of 11.955111.
Example 3
Consider the function f(x) = 27x. Plot the square super-root for this function over the range x = [0, 1].
Solution
The calculator plots the following:
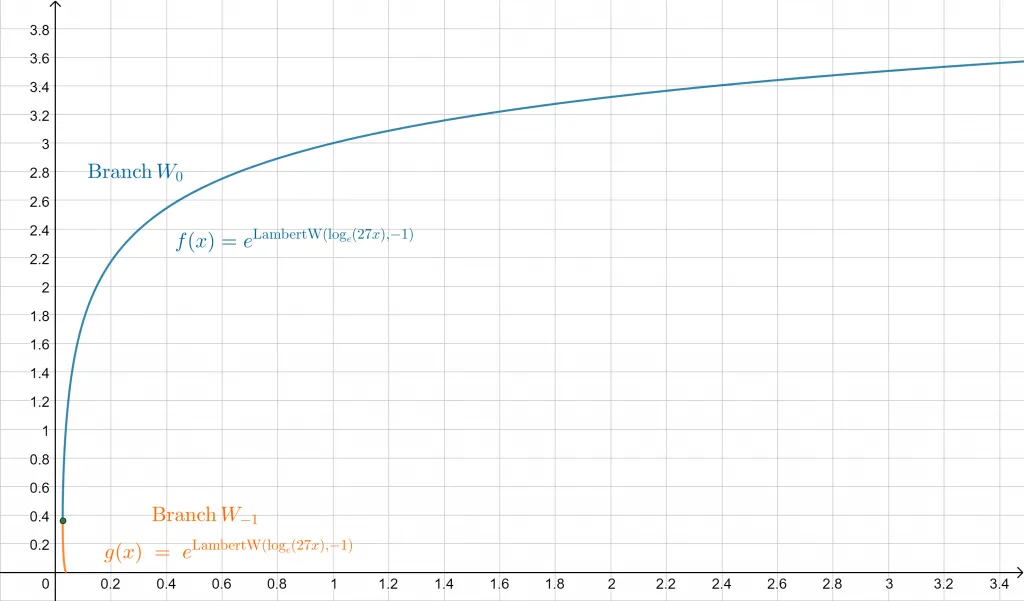
Figure 1
All graphs/images were created with GeoGebra.
