JUMP TO TOPIC
Linear Interpolation Calculator + Online Solver With Free Steps
The Linear Interpolation Calculator is an online tool that helps find the point between linearly associated discrete points. The calculator simply takes the information regarding the slope of the line, the first point, and the interpolation point.
The calculator’s output is the y-coordinate of the target interpolation point and number line representation for this point.

What Is a Linear Interpolation Calculator?
A Linear Interpolation Calculator is an online tool that can be used to calculate the coordinates of an interpolation point in discrete data points.
Whenever there is a need to find new points between a known set of points, the linear interpolation technique is used. In this method, it is assumed that points have linear relations and a single line passes between the known points.
Using this line, new points in a predefined range are estimated. It is used in multiple areas like in machine learning for making new data and making predictions, similarly to scale the data and make complex data into simpler ones.
It is very easy to find a single point using linear interpolation as it simply requires implementing a simple formula. But when you need to calculate a large number of new points, then it becomes very difficult to perform the calculation again and again. You can avoid going through this tiring process by using this excellent calculator. It is one of the best online available tools because it is free of cost and easy to use.
Anyone can access this tool via using their browser from anywhere and at any time. Unlike other modern tools, it does not require any installation or downloading process. It gives state-of-the-art performance by providing 100% accurate solutions.
It is a very useful tool, especially for students, mathematicians, and machine learning researchers where they can get solutions for their complex problems in a couple of seconds. The coming sections cover the procedure of using the calculator and its working mechanism.
How To Use the Linear Interpolation Calculator?
You can use the Linear Interpolation Calculator by inserting the elements required by the tool in their labeled fields. All you need is to enter these elements and use a button, the entire results will be provided to you.
The interface of the calculator is designed to be as user-friendly as possible so that anyone can comfortably use this tool even if he is using it for the very first time.
The procedure to use the calculator is explained in the detail below. It is mandatory to follow each of the given steps to get the correct results.
Step 1
Enter the first point of your data in the ‘Value A’ field. It has two boxes; enter the x-coordinate of the point in the left box and the y-coordinate in the right box.
Step 2
Now in the next field with the label ‘Value B’ put the x-coordinate of the interpolation point. It is the point at which you want to interpolate.
Step 3
Then insert the slope of the line that connects all the points in the ‘Range’ box. It should be in the range of 0 to 1. It describes the linear relation between the points.
Step 4
After putting all these elements, once again check the input and click the ‘Submit’ button.
Output
The solution is presented in a stepwise manner. First, it displays the inputs entered by putting the values in the formula for performing linear interpolation. Then it provides the value of the calculated y-coordinate of the interpolation point.
After this, the calculator graphically represents the calculated point using the number line graph. It is the location of the resultant point in its single plane.
It also displays the formula in the rational form where each term is written in its respective fraction. At last, it performs a short comparison between the y-coordinate of the given point and the y-coordinate obtained as result.
How Does the Linear Interpolation Calculator Work?
The linear interpolation calculator works by finding the interpolated value for the given data points on a line. It also plots the interpolated point on a number line. A required interpolated value can be found using this calculator by inputting the given x-y coordinates, the slope, and the point to perform the interpolation.
The usage of a linear interpolation calculator will be clear by first understanding the concept of interpolation and its types.
What Is Interpolation?
Interpolation is the technique of finding new data points in the range of known data points. It is useful to find the data points that are in between the known data points. It has many real-time applications such as predicting rainfall, noise level, or elevation.
The interpolation method helps to approximate the data values in those scenarios where the exact points are difficult to find and used to fill the gaps in data. It is the technique of curve fitting through the known values to define the function.
This process of interpolation is also widely used in engineering and science to fit the values of continuous sets or to derive an unknown formula. There are different types of interpolation which are listed below:
- Linear interpolation method
- Nearest neighbor interpolation
- Cubic spline interpolation method
- Shape preservation method
- Thin plate spline method
- Biharmonic interpolation method
Of the above-listed methods, the polynomial interpolation method, and spline interpolation method are the most commonly used due to their less consumption of memory and the accuracy of results.
However, this calculator is all about the Linear interpolation method and the explanation is given in succeeding headings.
Linear Interpolation
The linear interpolation method is used to generate distinct linear polynomials within the pairs of data points for a line or a curve or in between the set of three points. This technique is straightforward and provides perfect analytic results.
The linear interpolation makes use of a straight line to join the given set of data values in the positive and the negative direction of the unknown point.
If the data points are changed by a greater value then it will not give a good approximation since it does not give accurate results for the non-linear data. This method is applicable for data prediction, data forecasting, and market research.
Linear Interpolation Formula
The linear interpolation formula is the easiest way to find the estimated value of a function that is in between two known values. The formula is given below:
\[ \text{Linear Interpolation (y)}= y_1 + \frac{(y_2-y_1)}{(x_2-x_1)}(x-x_1)\]
Where,
- x1 and y1 are the 1st coordinates
- x2 and y2 are the 2nd coordinates
- x is the point of consideration for which interpolation is performed
- y is the required interpolated value
This calculator calculates the interpolated value by the reduced form of the above formula which is given as:
Linear Interpolation (y)= y1 + m (x-x1)
Where ‘m’ is the given slope or range.
Application of Interpolation
Interpolation has many applications, some of which are explained here. If there is a discrete set of data points {(xi, yi)} but the supposition is that the data points are obtained from a continuous function.
Then the coefficients {aj} of the function can be found by solving a system of linear equations that are acquired by the given data points and then evaluating the function within those data values.
Interpolation is also used to approximate the function f(x) with the help of polynomial or piecewise polynomial functions p(x). In this way, the differentiation or integration of the actual function f(x) becomes simple.
Solved Examples
Here are some problems related to linear interpolation solved by the calculator. Each problem is briefly discussed below.
Example 1
A basketball association needs players for the Olympics competition. The players of different heights are placed at different locations in ascending order of height. The locations of players and their heights are defined in the table below:
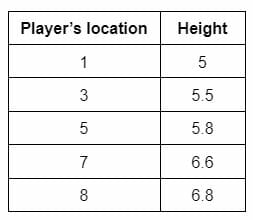
Figure 1
Find the estimated height of the player located at the sixth spot.
Solution
This problem is of linear growth therefore the estimated height can easily be calculated using a linear interpolation calculator.
In this example, we have x1 = 5, y1 = 5.8, x2=7, y2 = 6.6 and x = 6. The slope ‘m’ or range is found by:
\[m = \frac{6.6-5.8}{7-5}\]
m = 0.4
Now, the estimated height can be calculated by inserting the range, x1, y1 coordinates, and the point ‘x’ to perform interpolation in the calculator and it gives the following results.
Input
The formula after inserting the value is as follows:
5.8 + 0.4 (6 – 5)
Result
y = 6.2
Hence, the approximated height of the player located at the sixth spot is 6.2 feet.
Number Line

Figure 1
Rational Form
The rational form for the above formula is shown below:
31/5 = 6 + 1/5
Percent Increase
Here is a short comparison.
5.8 + 0.4(6-5)= 6.2 is 6.89655% larger than 5.8
Example 2
Calculate the value of y if x = 20, and some data points are given as (10, 12) and (30, 26). Use the linear interpolation technique to find the y-coordinate.
Solution
First, we need to calculate the slope of the line that passes through both given points.
\[ m = \frac{26 – 12}{30 – 10} = 0.7 \]
Now the calculator takes the first point as a reference which is P(10, 26) and gives the following solution.
Input
The input values are inserted in the formula and given below:
12 + 0.7 (20 – 10)
Result
The y-coordinate for x = 20 is given as follows:
y = 19
Number Line
The number line representation for the resultant point is given below in figure 2.

Figure 2
