JUMP TO TOPIC
Maximum and Minimum Calculator + Online Solver With Free Steps
The Maximum and Minimum Calculator is an online widget that helps to find the maximum and minimum values of a function. The calculator only accepts the mathematical function to deliver the solution.
The maximum value is the point at which the function has the highest value of all other values while the minimum value is the lowest value throughout the function.
The calculator returns the global maximum and minimum of the function along with a graph in the cartesian plane as a solution.

What Is a Maximum and Minimum Calculator?
A Maximum and Minimum Calculator is an online calculator that can be used to determine the maximum and minimum values of a mathematical function.
The process of finding the extreme values of function is also known as optimization. Optimizing the function is a core concept in the domains of engineering, business, and machine learning.
It has various applications, such as determining the maximum area, the least expenditure on projects, increasing missile range, and many more like that.
To find extreme values of the function manually, one needs to perform the derivative tests and extract the critical points. For this, you should be quite knowledgeable in derivative-related topics. Moreover, it is a tough process that requires time and effort.
However, you can avoid this hassle with the help of the Maximum and Minimum Calculator. It swiftly determines the target function’s global extremum and provides a graphical illustration of the function for easier comprehension.
How To Use the Maximum and Minimum Calculator?
You can use the Maximum and Minimum Calculator by directly entering the function and specifying either to maximize or minimize it. The user can easily navigate through the calculator to get output as its interface is quite simple.
The calculator is not only easy to use, but it can find extreme values for a variety of functions such as algebraic, exponential, and trigonometric functions. It can take only one function at one time to optimize.
For a more enhanced understanding, given below is a detailed procedure for using the Maximum and Minimum Calculator.
Step 1
Specify the optimization type according to your problem. The calculator has two options that are Maximize and Minimize in the “Find the” box. Select the appropriate option among one of these.
Step 2
Then in the next tab with the label “of” insert the target function.
Step 3
To get the final answer click the Submit button.
Output
The calculator processes the function and displays the output in multiple windows. First, it shows the input interpretation that shows the optimization type and the function. It enables the user to double-check the input to ensure the results are error-free.
Then it returns the desired global extreme of the function. It can be either the maximum or minimum whatever the user selected. It is to be noted that if a function does not have a global extreme then it will return a local extreme in that case.
The last section graphically depicts the input function in the x-y plane. It indicates the location of the global extremum by representing it as a distinct point on the function line.
How Does the Maximum and Minimum Calculator Work?
The Maximum and Minimum Calculator works by taking the input function and identifying the stationary points, one being the global maximum or minimum. It uses the principle of derivative to find the stationary points.
To develop a better understanding of the functionality of the calculator, let’s review some important concepts.
What Is a Stationary Point?
A stationary point is a point at which the derivative of the function becomes equal to zero. The stationary point for mathematical functions f(x) can be represented as:
f’(x) = $\frac{d}{dx}$f(x) = 0
Now let’s discuss all the extreme points of a function one by one.
Local Extremum
The local extremum is a relative point when we have multiple extremes. The local minimum is a point at which the function has relatively less value than the value at surrounding points. A point b is the local minimum if f(b) < f(x).
Whereas a local maximum is a point at which function has a relatively greater value than surrounding points.A point b is the local maximum if f(b) > f(x). Here x represents surrounding points and there can be multiple local extrema.
Global Extremum
The global extremum is one and absolute extremum throughout the whole function. The global minimum is the point at which the function has the lowest value of all the other values. A point d is the global minimum if $f(d) \le f(x)$.
Likewise, the point at which a function has the greatest value than values at all other points is said to be a global maximum. A point d is the global maximum if $f(d) \ge f(x)$. Here x represents all the remaining values of the interval.
Finding Maximum and Minimum
There are two methods to find the extreme values of a function.
First Method
The first method is to find the first derivative of the function then the points at which the derivative becomes zero. It can be represented as:
f’(x) = 0
To find relative extrema, simply put the adjacent points from both sides. If the function is increasing before and decreasing after the point, then it is maximum and if decreasing before and increasing after the point, then it is minimum.
Calculate the values of the function at all these points and ends of the interval. The point at which the largest value is obtained is the global maximum and the lowest value is the global minimum.
The second method includes two steps. The first step is to determine the stationary point at which the first derivative is zero. Then calculate the second derivative at the same stationary points.
The point at which the second derivative is positive (f’’(x) > 0) is the minimum and the point for which it is negative (f’’(x) < 0) is the maximum. In the case of multiple values, for global extremum check the largest or smallest value.
Solved Examples
Some examples solved by the calculator are given below.
Example 1
A store keeper wants to increase the profit of his store. The profit function is given as:
\[ f(x) = 2x^{2} – 8x^{4} \]
Find maximum profit he can earn.
Solution
The solution to the problem is given as:
Global Maxima
\[ max\, \{2x^{2} – 8x^{4} \} = \frac{1}{8} \, at \, x = – \frac{1}{2\sqrt{2}} \]
\[ max\, \{2x^{2} – 8x^{4} \} = \frac{1}{8} \, at \, x = \frac{1}{2\sqrt{2}} \]
Plot
The graphical illustration for the function is given in figure 1.
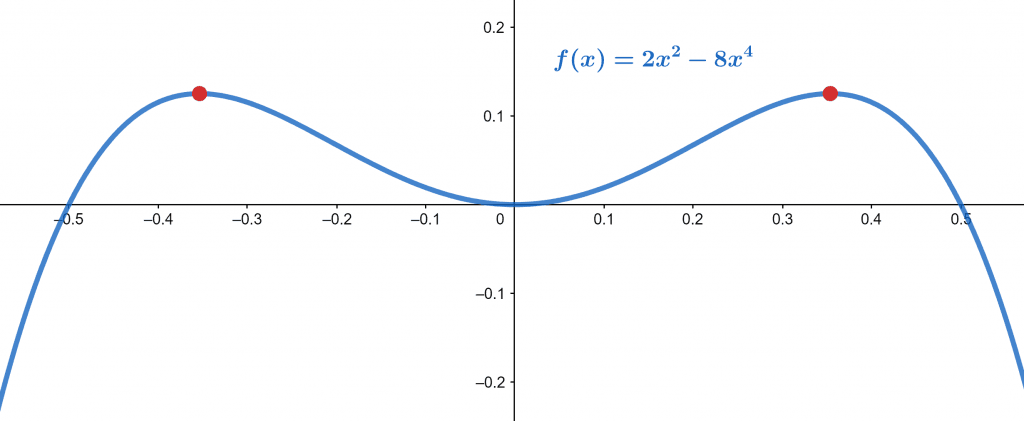
Figure 1
Example 2
Consider the following function:
\[ f(x) =x^{2} – 4x \]
Find the minimum of the function using the calculator.
Solution
The solution can be easily obtained using the Maximum and Minimum Calculator.
Global Minima
\[ max\, \{x^{2} – 4x \} = – 4 \, at \, x = 2 \]
Plot
Figure 2 highlights the position of the minimum on the function graph.
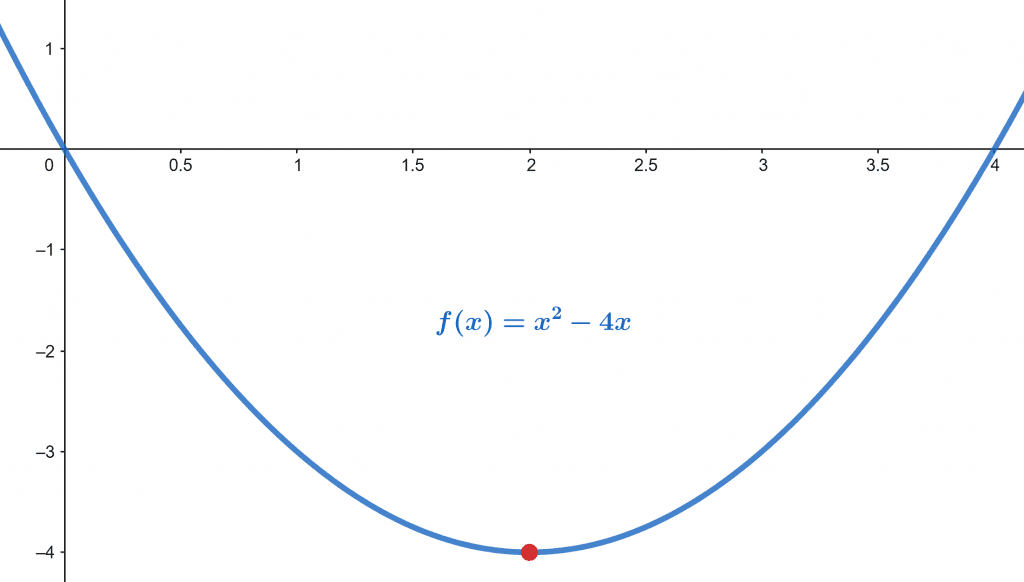
Figure 2
All the Mathematical Images/Graphs are created using GeoGebra.
