JUMP TO TOPIC
Slant Asymptote Calculator + Online Solver With Easy Steps
The online Slant Asymptote Calculator is a calculator that helps you plot a graph from an asymptomatic slant value.
The Slant Asymptote Calculator is helpful for mathematicians and scientists as it helps them quickly solve and plot complex polynomial fractions.

What Is a Slant Asymptote Calculator?
A Slant Asymptote Calculator is an online calculator that solves polynomial fractions where the degree of the numerator is greater than the denominator.
The Slant Asymptote Calculator requires two inputs; the numerator polynomial function and the denominator polynomial function.
After inputting the values, the Slant Asymptote Calculator uses these polynomial fractions to calculate the slant asymptote. The Slant Asymptote Calculator also plots a graph for these values.
How To Use a Slant Asymptote Calculator?
To use the Slant Asymptote Calculator, enter the input values the calculator requires and click the “Submit” button.
The step-by-step instructions for using the calculator are given below:
Step 1
First, in the numerator, you enter the polynomial function that is provided to you. Make sure that the numerator is one degree higher than the denominator function.
Step 2
After entering the polynomial function into your numerator, you input the denominator polynomial function into its respective box.
Step 3
Once you enter both the numerator and denominator values, you click on the “Submit” button present on the Slant Asymptote Calculator. The calculator finds the slant asymptote values and plots a graph in a new window.
How Does a Slant Asymptote Calculator Work?
A Slant Asymptote Calculator works by taking in the input values and applying long division or synthetic division to the polynomial fraction. This results in calculating the slant asymptote value of the fraction.
The following equation can be used to represent the slant asymptote polynomial:
y = f(x) = $\frac{N(x)}{D(x)}$ , where N(x) and D(x) are polynomials
What Is Asymptote of a Curve?
An asymptote of a curve is the line created by the curve’s motion and a line that is continuously going towards zero. This may occur if the x-axis (horizontal axis) or y-axis (vertical axis) moves toward infinity. An asymptote is a line that a curve approaches as it travels towards infinity (without touching it).
The curve and its asymptote have an odd and unique relationship. At any point in infinity, they run parallel to one another yet never cross paths. They are separated while running extremely close to one another.
There are three types of asymptote:
- Horizontal Asymptote – The form equation is y=k
- Vertical Asymptote – The form equation is x = k
- Slant Asymptote – The form equation is y = mx + c
Slanted Asymptote
Slanted asymptotes are often referred to as oblique asymptotes due to their slanted shape, representing a linear function graph, y = mx + c. Only when the degree of the numerator exceeds the degree of the denominator by precisely one degree can a rational function have a slanted asymptote.
As seen by the example below, we can predict the final behavior of rational functions using slanted asymptotes:
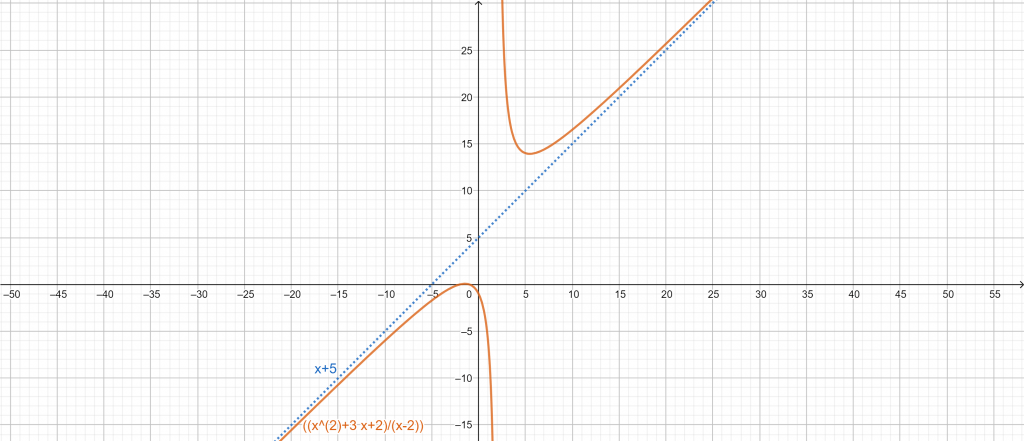
Figure 1
The graph in Figure 1 shows that the slanted asymptote of f(x) is represented by a dashed line that controls the graph’s behavior. Additionally, we can see that x+5 is a linear function with the form y=mx+c.
Looking at the slanted asymptote, we can see how the curve of f(x) behaves as it approaches $\infty$ and $-\infty$. Also confirmed by the graph of f(x) is what we already know: slanted asymptotes will be linear (and slanted).
Finding Slanted Asymptotes
We must be familiar with two crucial techniques to find the slanted rational asymptote.
- Long divisions on polynomials
- Synthetic division on polynomials.
The results of both approaches should be the same; the choice between the two will only depend on the numerator and denominator forms.
We may calculate the quotient of $ \frac{N(x)}{D(x)}$ to discover the oblique asymptote because $f(x) = \frac{N(x)}{D(x)}$ is a rational function with N(x) being one degree greater than D(x). We get the following equation:
f(x)= Quotient + $\frac{Remainder}{D(x)}$
We only consider the quotient and ignore the remainder when determining the slanted asymptote.
Rules for Calculating Slanted Asymptotes
Some rules must be followed when calculating the slanted asymptote for a polynomial function.
We always verify whether a function has a slanted asymptote when determining the slanted asymptote of a rational function by looking at the degrees of the numerator and denominator. Make sure the degree in the numerator is precisely one degree higher.
The function’s slanted asymptote will be its simplest form if the numerator is a multiple of the denominator. For example, we have a function $f(x)= \frac{x^{2}-16}{x-4}$. In factored form, $x^{2}-16$ is equivalent to (x-4)(x+4), therefore the denominator is a factor of the numerator.
The simplified form of the equation is as follows:
\[ f(x)=\frac{\cancel{(x-4)}(x+4)}{\cancel{(x-4)}}=(x+4) \]
This means that the slant asymptote of the function is y=x+4.
Use long division or synthetic division to get the function’s quotient if the numerator is not a multiple of the denominator. Suppose we have the following equation:
\[ f(x)= \frac{x^{2}-6x+9}{x-1} \]
f(x) must have a slanted asymptote because we can observe that the numerator has a more significant degree (precisely one degree). By using synthetic division, we find the quotient of the function, which is x-5. Using these two methods, we can calculate the slanted asymptote, y=x-5.
Solved Examples
The Slant Asymptote Calculator instantly provides you with the slant asymptote of a polynomial fraction.
Here are some examples solved using a Slant Asymptote Calculator:
Example 1
While completing his assignment, a college student comes across the following equation:
\[ f(x)= \frac{x^{2}-5x+10}{x-2} \]
The student must find the slant asymptote of the polynomial function given above. Use the Slant Asymptote Calculator to solve the equation.
Solution
We can use the Slant Asymptote Calculator to solve the polynomial fraction quickly. First, we enter the polynomial with the higher degree into the numerator box, which is $x^{2}-5x+10$. After entering the first polynomial, we enter the second polynomial equation in the denominator box; the equation is x-2.
Once we input all the equations in the Slant Asymptote Calculator, we click the “Submit” button. The calculator computes the results and displays them in a new window.
The following results shown below are extracted from the Slant Asymptote Calculator:
Input Interpretation:
\[ Oblique \ asymptotes: \ y= \frac{x^{2}-5x+10}{x-2} \]
Results:
\[ y= \frac{x^{2}-5x+10}{x-2} \ is \ asymptotic \ to \ x-3 \]
Plot:
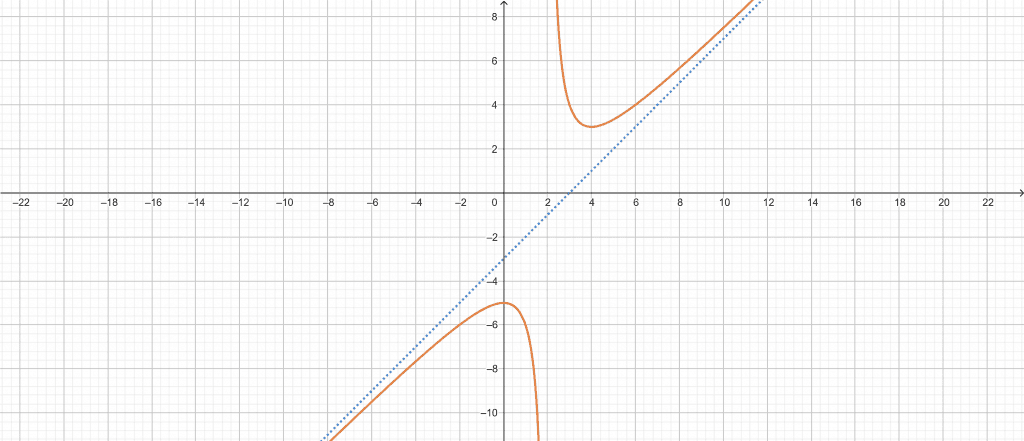
Figure 2
Example 2
A scientist, while conducting an experiment, needs to find the slant asymptote value of the following polynomial fraction:
\[ f(x) = \frac{x^{2}-6x}{x-4} \]
Using the Slant Asymptote Calculator, find the slant asymptote value of the polynomial fraction.
Solution
Using the Slant Asymptote Calculator, we can instantly find the asymptomatic slant value of a polynomial fraction. First, we input the higher degree polynomial in the numerator box; the polynomial value is $x^{2}-6x$. After entering the first polynomial equation, we enter the second polynomial function into the denominator box; the polynomial function is x-4.
After all the inputs are added to the Slant Asymptote Calculator, we click the “Submit” button on our Slant Asymptote Calculator. The calculator will start its calculation and quickly displays the asymptomatic slant value along with its graphical representation.
The following results are calculated using the Slant Asymptote Calculator:
Input Interpretation:
\[ Oblique \ asymptotes: y= \frac{x^{2}-6x}{x-4} \]
Results:
\[ y= \frac{x^{2}-6x}{x-4} \ is \ asymptotic \ to \ x-2 \]
Plot:
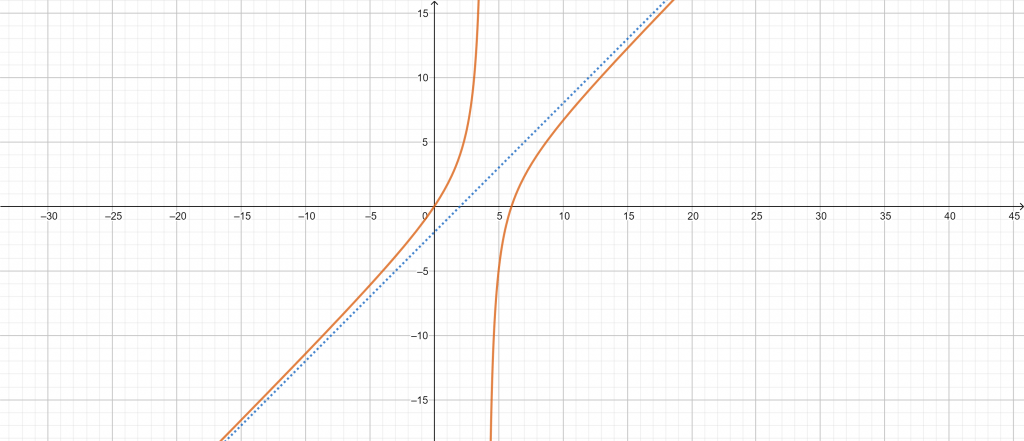
Figure 3
Example 3
While solving a complex mathematical problem, a student must compute a polynomial fraction’s slant asymptote value. The equation is as follows:
\[ f(x) = \frac{x^{2}-7x-20}{x-8} \]
Using the Slant Asymptote Calculator, find the asymptomatic slant value of the polynomial fraction above.
Solution
With the help of the Slant Asymptote Calculator, we can calculate the slant asymptote value of the polynomial equations. Initially, we plug the higher degree polynomial in the numerator box on the Slant Asymptote Calculator; the polynomial equation is $x^{2}-7x-20$. After the numerator’s polynomial equation, we add the second polynomial equation into the denominator box; the polynomial equation is x-8.
Finally, after entering the polynomial equations into the Slant Asymptote Calculator, we click the “Submit” button. The calculator calculates the slant asymptote values, and a graph is plotted for the polynomial equations.
Below are the results from the Slant Asymptote Calculator:
Input Interpretation:
\[ Oblique \ asymptotes: y = \frac{x^{2}-7x-20}{x-8} \]
Results:
\[ y = \frac{x^{2}-7x-20}{x-8} \ is \ asymptotic \ to \ x-1 \]
Plot:
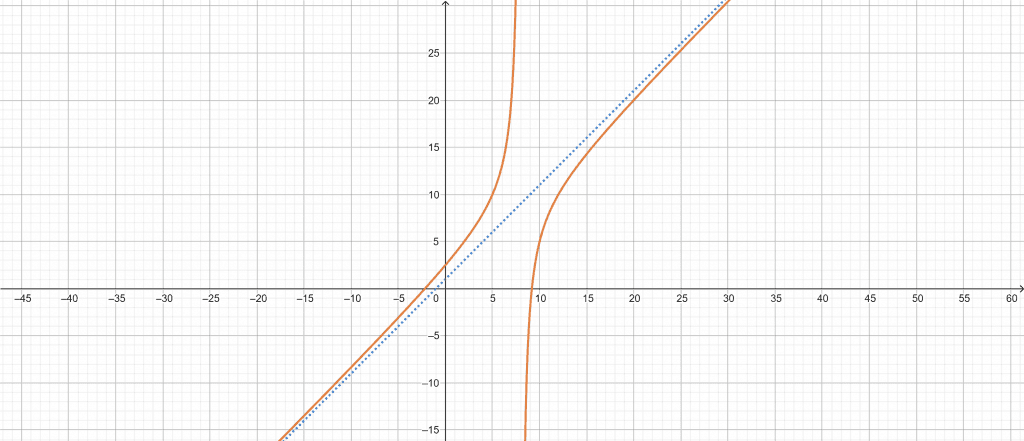
Figure 4
Example 4
Consider the following polynomial fraction:
\[ f(x) = \frac{x^{2}+3x-10}{x-1} \]
Find the slant asymptote of the polynomial fractions above.
Solution
To find the slant asymptote, we can use the Slant Asymptote Calculator. Initially, you input the first polynomial equation into the numerator box. Then you enter the second polynomial equation into the denominator box.
Finally, you click the “Submit” button on the calculator. The Slant Asymptote Calculator computes the results and displays them in a window.
The following results are from the Slant Asymptote Calculator:
Input Interpretation:
\[ Oblique \ asymptotes: y = \frac{x^{2}+3x-2}{x-1} \]
Result:
\[ y = \frac{x^{2}+3x-10}{x-1} \ is \ asymptotic \ to \ x + 4 \]
Plot:
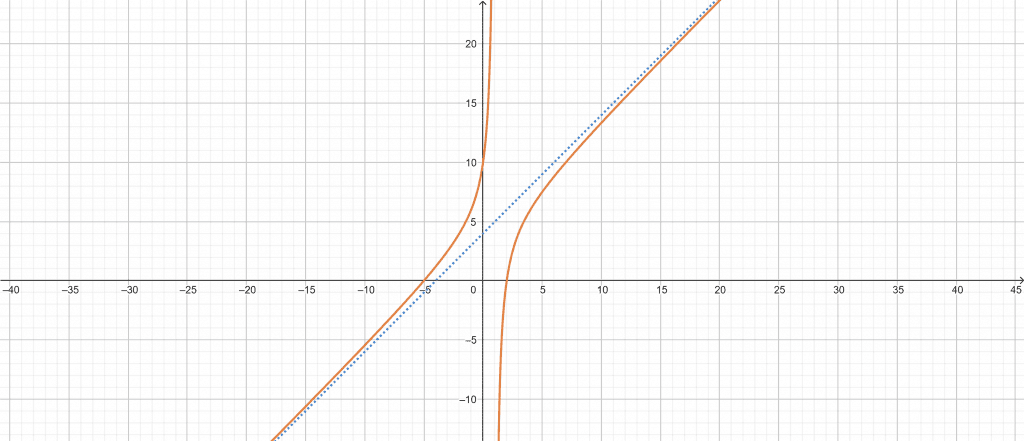
Figure 5
All Images/Graphs are made using GeoGebra.
