JUMP TO TOPIC
Multiplicity Calculator + Online Solver With Free Steps
The online Multiplicity Calculator allows you to find the zeros of an equation.
The online Multiplicity Calculator is a powerful tool used by mathematicians and physicists to find the zeros or roots of an equation. The Multiplicity Calculator plays a vital role in solving complex mathematical problems.

What Is a Multiplicity Calculator?
A Multiplicity Calculator is an online calculator that allows you to find the zeros or roots of a polynomial equation you provide.
The Multiplicity Calculator requires a single input, an equation you provide to the Multiplicity Calculator. The equation must be a polynomial function for the Multiplicity Calculator to work. The Multiplicity Calculator calculates the results instantly and displays them in a new window.
The Multiplicity Calculator displays several results such as the roots of the equation, root plot of the equation, number line of the equation, the sum of roots, and the product of roots.
How To Use a Multiplicity Calculator?
You can use the Multiplicity Calculator by entering your polynomial equation and clicking the “Submit” button. The results would be instantly displayed on your screen.
The step-by-step instructions on how to use a Multiplicity Calculator are given below:
Step 1
In the first step, you plug your polynomial equation into the input box provided in your Multiplicity Calculator.
Step 2
After entering your polynomial equation in the Multiplicity Calculator, you click the “Submit” button. The calculator will display the results in a separate window.
How Does a Multiplicity Calculator Work?
A Multiplicity Calculator works by calculating the zeros or the roots of a polynomial equation. A polynomial equation $ax^{2} + bx + c $ usually intercepts or touches the x axis of a graph; the equations are solved and are put equal to zero to calculate the roots of the equation.
Let’s discuss some important concepts related to the working of this calculator.
What Are Zeros of Polynomials?
Zeros of polynomials are points where the polynomial equations become equal to zero. In layman’s terms, we can state that a polynomial’s zeros are variable values at which the polynomial equals 0.
The zeros of a polynomial are often referred to as the equation’s roots and are frequently written as $\alpha$,$\beta$, and $\gamma$.
In mathematical terminology, the values of x that fulfill the polynomial f(x) = 0 equation are the zeros of polynomial. In this case, the polynomial’s zeros are the x values for which the function’s value, f(x), equals zero. The degree of equation f(x) = 0 determines how many zeros a polynomial has.
How To Find Zeros of Polynomials?
You can find zeros of the polynomial by substituting them equal to 0 and solving for the values of the variable involved that are the zeros of the polynomial.
Finding a polynomial’s zeros can be done in a variety of ways. The degree of the polynomial equation determines how many zeros the polynomial has.
To determine the zeros of the polynomial, each of the numerous equations—which have been categorized as linear, quadratic, cubic, and higher degree polynomials—is individually examined.
The different polynomial equations with the methods to solve them are given below:
Finding Zeros for Linear Equations
Linear equations are generally written as y = ax + b. You may find the solution to this equation by substituting y = 0, and when we simplify, we get ax + b = 0, or $x = \frac{-b}{a} $.
Finding Zeros for Quadratic Equations
A quadratic equation can be factored in by using either of the two methods. It is possible to factor the quadratic equation of the type $x^{2} + x(a + b) + ab = 0$ as (x + a)(x + b) = 0, with the polynomial’s zeros being x = -a and x = -b.
And since the zeros in a quadratic equation of the type $ax^{2}+ bx + c = 0$ cannot be factorised, the formula approach can be used to get the zeros is $ x = \frac {[-b \pm \sqrt{(b^{2}-4ac)}]}{2a}$.
Finding Zeros for Cubic Equations
By using the remainder theorem, the cubic equation of the form $y = ax^{3} + bx^{2} + cx + d$ can be factorized. The variable x = $\alpha$ can be replaced with any lower values according to the remainder theorem, and if the value of y results in zero, y = 0, then the (x – $\alpha$ ) is one root of the equation.
We can divide the cubic equation by $(x – \alpha )$ using long division to create a quadratic equation.
The quadratic equation can finally be solved using either the formula approach or factorization to achieve the required two roots for the quadratic equation.
Finding Zeros for Higher Degree Polynomials
Higher degree polynomials can be factorized using the remainder theorem to create a quadratic function. Higher degree polynomials are generally represented as $y = ax^{n}+ bx^{n-1}+cx^{n-2} + ….. px + q$.
After calculating the quadratic formula from these higher-degree polynomials, they can be factorized to obtain the roots of the equation.
What Is a Multiplicity of Polynomial?
The multiplicity of a polynomial means the number of times the root values appear in a polynomial equation. If we have the factored version of the polynomial, figuring out the number of roots is simple. Alternately, it is also feasible to ascertain the number of roots by examining the polynomial graph.
The $x$-intercepts of the polynomial’s graph are the real roots of the polynomial. As a result, we can learn how many real roots it has by examining a polynomial graph.
Similarly, by examining the polynomial’s zeros or its factored form, we may predict how often the graph will touch or cross the x-axis. The multiplicity of a zero or a root is the number of times its related factor appears in the polynomial.
For example, a quadratic equation (x+5)(x-3) has the root x= -5 and x = 3. This explains that the line of the equation passes through x= -5 and x = 3 once.
If the polynomial is not factored in, we must factor it or obtain a graph of the polynomial to examine how it behaves while crossing or contacting the x-axis.
Solved Examples
The Multiplicity Calculator is an efficient way to calculate the zeros or roots of a polynomial equation.
Here are some solved examples that are solved using a Multiplicity Calculator.
Solved Example 1
A high school student is given the following polynomial equation:
\[ 3x^{2} – 6x \]
The student must figure out the zeros and create a graph using this polynomial equation. Find the zeros and plot a graph using the polynomial equation.
Solution
Using the Multiplicity Calculator, we can calculate the zeros of the polynomial equation and plot a graph. First, we enter the polynomial equation into the Multiplicity Calculator.
After entering the polynomial equation, we click the “Submit” button on the Multiplicity Calculator. The calculator opens a new window and displays the results of our equation.
The results from the Multiplicity Calculator are given below:
Input interpretation:
\[ Roots \ 3x^{2} – 6x = 0 \]
Results:
x = 0
x = 2
Root Plot:
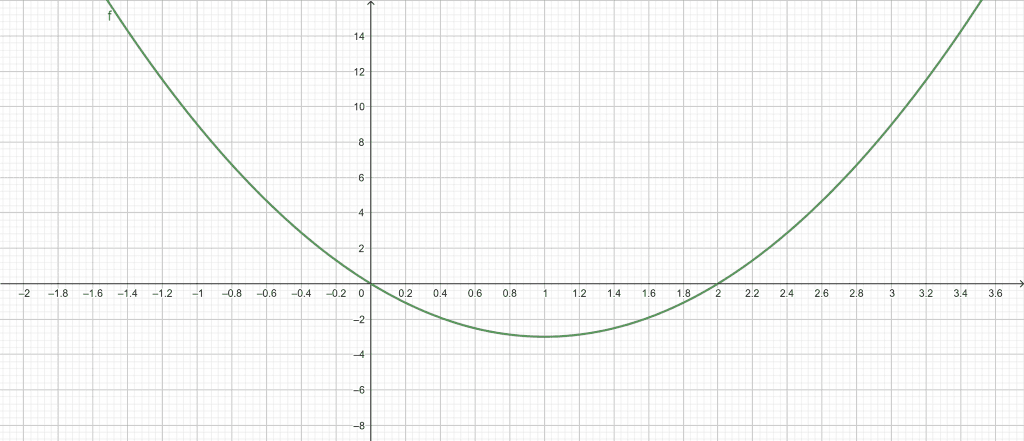
Figure 1
Number Line:
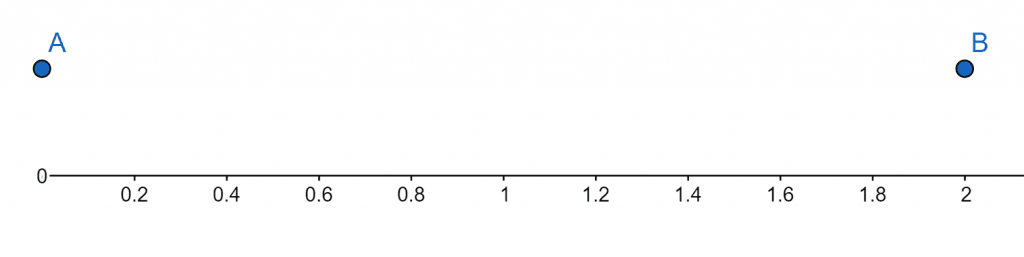
Figure 2
Sum of Roots:
2
Product of Roots:
0
Solved Example 2
While researching, a mathematician comes across a higher degree polynomial equation $y = x(x+1)^{2}(x+2)^{3}$. To complete his research, the mathematician needs to find the roots of the polynomial equation.
Find the roots of the higher degree polynomial.
Solution
To solve the equation and find the roots by using the Multiplicity Calculator, first we plug in the polynomial equation we are provided into its respective input box.
After plugging in the polynomial equation, all we need to do is click the “Submit” button on the Multiplicity Calculator. The Multiplicity Calculator instantly provides the result for the polynomial equation.
The following are the results calculated by the Multiplicity Calculator:
Input interpretation:
\[ Roots \ x(x+1)^{2}(x+2)^{3} = 0 \]
Results:
x = -2 (multiplicity 3)
x = -1 (multiplicity 2)
x = 0 (multiplicity 1)
Root plot:
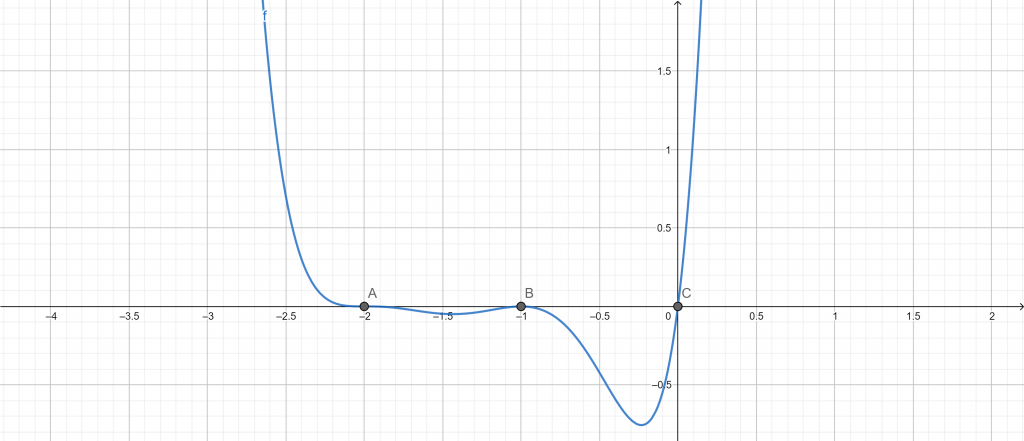
Figure 3
Number Line:
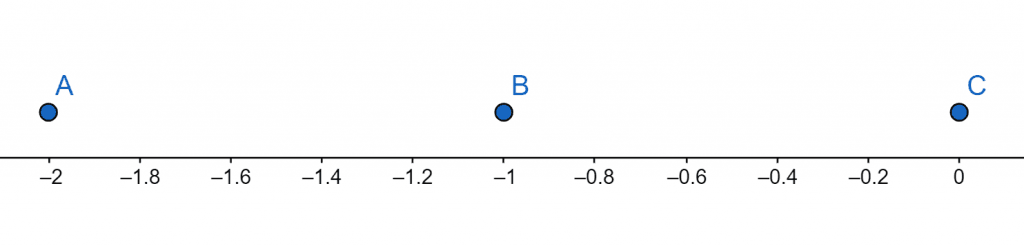
Figure 4
Sum of Roots:
-8
Product of Roots:
0
Solved Example 3
While working on an assignment, a college student stumbled upon the following equation:
\[ y = \frac{1}{6} (x-1)^{3}(x+3)(x+2) \]
The student must find the multiplicity of zeros in the polynomial equation. Find the multiplicity of zeros of the polynomial equation given.
Solution
We can use the Multiplicity Calculator to find the multiplicity of zeros of the polynomial equation. To use the calculator, we first add the polynomial equation in the input box.
After adding the polynomial equation into the Multiplicity Calculator, we click the “Submit” button and let the calculator do its job. The Multiplicity Calculator provides us with the roots of the polynomial equation in a fraction of a second.
The results of the Multiplicity Calculator are given below:
Input Interpretation:
\[ Roots \ \frac{1}{6} (x-1)^{3}(x+3)(x+2) = 0 \]
Results:
x = -3 (multiplicity 3)
x = -2 (multiplicity 2)
x = 1 (multiplicity 1)
Root plot:
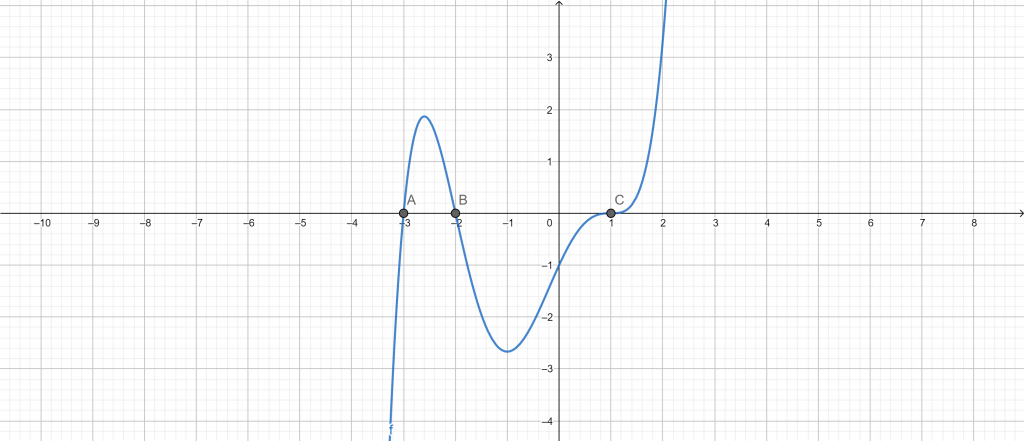
Figure 5
Number Line:
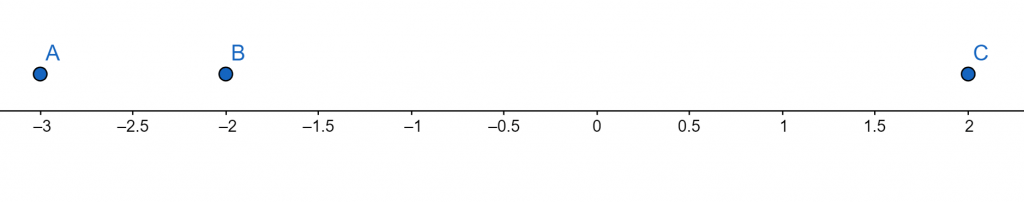
Figure 6
Sum of Roots:
-2
Product of Roots:
6
Solved Example 4
Consider the following polynomial equation:
\[ ( x + 3 ) ( x – 2 )^{2} ( x + 1 )^{3} \]
Using the equation above, calculate the multiplicity of zeros.
Solution
The Multiplicity Calculator can be used to find the multiplicity of zeros in the polynomial equation we are provided. To use the calculator, we enter the polynomial equation first.
Once we enter the polynomial equation, we click the “Submit” button on the Multiplicity Calculator.
The Multiplicity Calculator gives us the following results:
Input interpretation:
\[ Roots \ ( x + 3 ) ( x – 2 )^{2} ( x + 1 )^{3} = 0 \]
Results:
x = -3 (multiplicity 3)
x = -1 (multiplicity 2)
x = 2 (multiplicity 1)
Root plot:
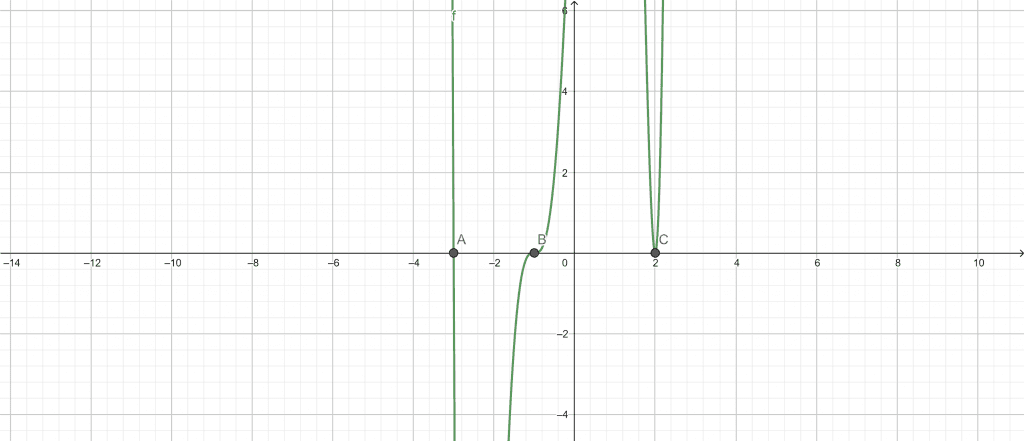
Figure 7
Number Line:
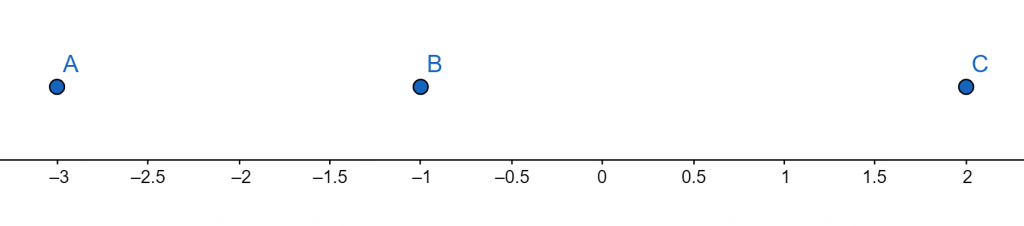
Figure 8
Sum of Roots:
-2
Product of Roots:
12
All images/graphs are created using GeoGebra.
