JUMP TO TOPIC
Multivariable Critical Point Calculator + Online Solver With Free Steps
The Multivariable Critical Point Calculator is a tool that is used to determine the local minima, local maxima, critical points, and stationary points by applying the power and derivative rule.
The critical point can be defined as the one in the function domain where the function is not differentiable or in case the variables are a bit too complex. It is the point where whether the first partial derivative of the function is zero or the function domain is not holomorphic (complex-valued function).

What Is the Multivariable Critical Point Calculator?
The Multivariable Critical Point Calculator is an online Calculator for solving complex equations and calculating the critical points. As the name suggests, the Multivariable Critical Point Calculator is used to find the critical points (also called the stationary points), the maxima and minima, and also the saddle point (the ones which are not a local extremum).
All maxima and minima and the tangent plane of points z=f(x,y) are horizontal and critical points.
In a few cases, the critical points might not be presented as well which is an indication that the slope of the graph will not change. In addition to this, the critical points on a graph can be increased or decreased by applying the method of differentiation and substitution of the value x.
In a function that has multiple variables, the partial derivatives (used to find the critical points) are equal to zero in the first order. The critical point is the point where the given function becomes undifferentiable. While dealing with the complex variables critical point of the function is the point where its derivative is zero.
Though finding the critical points is considered a tough job but plays a major role in math so you can easily find them using a few easy steps through the Multivariable Critical Point Calculator.
How To Use the Multivariable Critical Point Calculator?
Here is an easy-to-follow guideline on how to use the Multivariable Critical Point Calculator.
By applying these few simple steps you can find out multiple things using the Multivariable Critical Point Calculator e.g. the distance, parallel, the given slope and points, and the main thing, the critical points. Just make sure you have all the values to get the desired results.
Step 1:
Use the calculator to find the critical and saddle points for the given function.
Step 2:
You have to find the derivative using the calculator by putting in the correct values of x. If there are any values of $x$ that are still to be found in the function, you have to set the calculator as F(x).
Click on the button ‘Enter’ to get your answer after each step. The derivative will be found using the power rule through the calculator.
Step 3:
Next, if any values of x are mentioned you will find them where f ‘(x) will not be defined.
Step 4:
All of the values of x that will be in the domain of f(x) (refer to Step 2 and Step 3) are the x-coordinates of the critical points so the last step will be to find the corresponding y-coordinates which will be done by substituting each of them into the function y = f(x).
(Noting down each of the points and making pairs will give us all the critical points i.e. (x,y).)
How Does the Multivariable Critical Point Calculator Work?
The Multivariable Critical Point Calculator works by finding the x values for which the derivative of the given function is equivalent to zero and the x values for which the derivative of the function is undefined.
The Critical Point Calculator is also known as the saddle point calculator and can help us to solve multiple math functions with multiple variables. The calculator works by first calculating the derivate using the power rule for all the coordinates and then helps you find the critical points with great ease.
You can also create a graph using the found coordinates on the Critical Point Calculator.
What Are Critical Points and What Role Do They Play While Constructing Graphs?
In terms of the graphical representation, the points that form a vertical, horizontal tangent or do not exist at the given point on the drawn curve are known as critical points. Each point that has a sharp turning point can also be defined as a critical point.
Depending on the critical points the graph either decreases or increases which demonstrates how the curve might have been at a local minimum or a local maximum. It is a matter of fact that linear functions do not have critical points whereas the critical point of a quadratic function is its vertex.
In addition to this, as critical points are defined as the points where the first derivative vanishes the endpoints of graphs can never be the critical points.
What Is a Saddle Point and How Do You Calculate These Points Without a Calculator?
In the light of the saddle point in calculus, the saddle point is the point on the curve where the slopes are equivalent to zero and it is not the local extremum of the function (neither minima nor maxima).
The saddle point can also be calculated using the second partial derivative test. If the second partial derivative is less than zero, then the given point is regarded as a saddle point.
We can find out the critical points from a function but it can be difficult with complex functions. To find the saddle points without a calculator, you first need to calculate the derivative. Factor solving is the key to solving such questions quicker and by hand.
Now, that our derivative will be polynomial (will have variables and coefficients both) thus, the only critical points will be those values of X which is an instance that makes the derivative equivalent to zero.
Solved Examples:
Example 1:
Calculate the critical points for the following function using the calculator:
\[ f(x) = x^{3}+7x^2+16x \]
Solution:
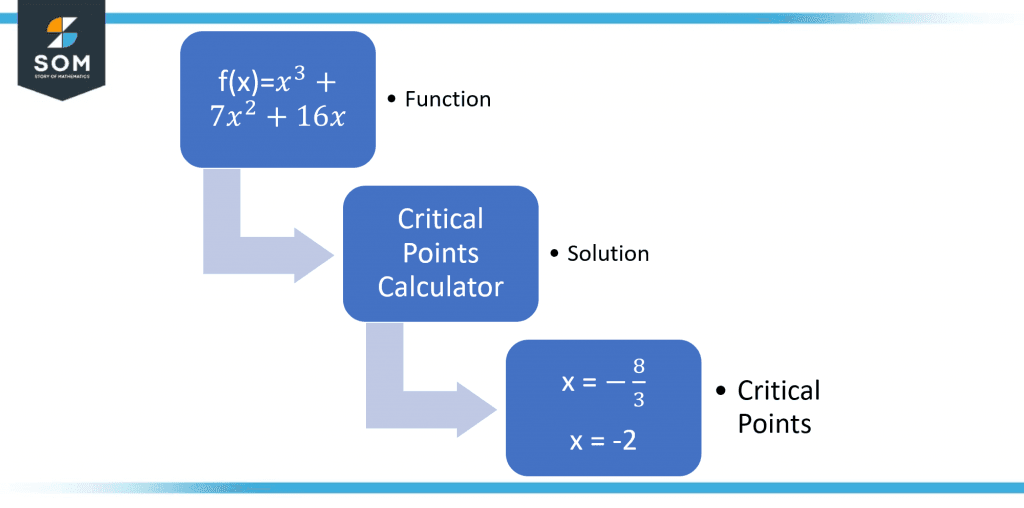
Figure 2 – Procedure of Critical Points
Differentiate the equation
\[ f(x) = x^{3}+7x^2+16x\]
term by term w.r.t x.
The derivative of the function is given as:
\[ f”(x) = 3x^2 + 14x + 16 \]
Now, find the values of $x$ such that f'(x) = 0 or f'(x) is undefined.
Put the equation in the calculator to find out the critical points.
After solving, we get:
\[ x = \dfrac{-8}{3} \]
x = -2
Plugging the value of x in the f(x) gives:
\[ f(x) = x^{3}+7x^2+16x\]
f(-8/3) = -11.85
f(-2) = -12
Since, the function exists at $x=-\dfrac{8}{3}$ and x=-2 therefore, $x = \dfrac{-8}{3}$ and x=-2 are critical points.
Example 2:
Find the critical points of the function:
\[f(x, y) = 3x^2+8xy+4y\]
Solution:
Partial Differentiate the equation
\[ f(x , y) = 3x^2+8xy+4y\]
term by term w.r.t x.
The partial derivative of the function is given as:
f”(x) = 6x + 8y
Now, find the values of $x$ such that f'(x) = 0 or f'(x) is undefined.
Put the equation in the calculator to find out the critical points.
After solving,
\[ x = \dfrac{-1}{2} \]
\[ y = \dfrac{3}{8} \]
Plugging the value of x in the f(x) gives:
\[ f(x,y) = 3x^2+8xy+4y\]
\[ f(-1/2 , 3/8 ) = \dfrac{3}{4} \]
Since, the function exists at $x=-\dfrac{1}{2}$ and $y=\dfrac{3}{8}$.
Therefore, the critical points are $x=\dfrac{-1}{2}$ and $y=\dfrac{3}{8}$.
