JUMP TO TOPIC
Zeros Calculator + Online Solver With Free Steps
A Zero Calculator is an online calculator for determining the zeros of any function including linear, polynomial, quadratic, trigonometric functions, etc. on the specified interval.
The calculated zeros can be real, complex, or exact. The zeros of the real or complex functions are the numerical values at which the function f(x) becomes zero, or in other terms can be written as:
f(x) = 0
such that x is the zero of the given function in the specified domain.

What Is the Zeros Calculator?
A Zeros Calculator is a calculator that can find the zeros of any type of function on any given interval, even the most complicated ones as well.
The Zeros Calculator helps to determine the zeros of the various functions on any given interval. The following is a list of different functions whose zeros can be computed easily and quickly by using this Zeros Calculator:
- Linear Functions
- Quadratic Functions
- Cubic Functions
- Polynomials
- Rational Value Functions
- Irrational Value Functions
- Exponential Functions
- Hyperbolic Functions
- Absolute Value Functions
Hence, the Zeros Calculator helps to solve tedious equations in just seconds. The Zeros Calculator finds the zeros of the given polynomial function with some additional features as well, including the root plot, the sum of the roots, and the product of the roots of the specified function.
How To Use the Zeros Calculator
Let’s discuss how to use the Zeros Calculator to find the zeros of any given function.
The Zeros Calculator helps to find the zeros of any kind of function easily. You can also find the zeros of any function manually, but it requires a lot of time and is a very lengthy procedure in terms of numerical calculations.
Figure-1 Methods to find Zeros
Therefore, with the help of this calculator, you can step toward your desired results smartly and save much more time. You just have to follow these simple steps to find the zeros of any function.
Step 1:
Use the Zero Calculator to find the zeros of the desired function.
Step 2:
There is an expression tab in the calculator. Input the function here for which the zeros are required to be calculated.
Step 3:
After you have entered the function for which you want to find the zeros, press the submit button placed just below the expression tab.
Step 4:
Once you have pressed the submit button, a new window will appear in front of you displaying the results. Zeros Calculator finds the zeros of the given function along with a root plot, zeros represented on a number line, sum of zeros, and product of zeros.
Step 5:
Lastly, for the detailed and step-by-step solution, you just have to click on the appropriate button given for the detailed solution and you can view the steps. If you want to find the roots of any other function, enter the new equation in the expression tab and follow the same procedure as mentioned above.
How Does a Zero Calculator Work?
A Zeros Calculator works by setting the function equivalent to zero and calculating the zeros. It works by segregating the variable x on one side of the equation or modifying the specified equation several times to find out all the zeros of the function. Let’s have a deep insight into the concept of function zeros.
Finding the roots or zeros of any type of function manually is very cumbersome and error-prone. There can be a polynomial with lots of roots that can be nearly impossible for you to calculate by hand, but this online zeros calculator has got you covered. You can calculate the zeros quickly by just simply entering the desired function into it.
What Is a Zero of a Function?
The zero of the function is the point that corresponds to the values of the variable of a function that when put in the function, the function becomes zero. Graphically, zero of the function is the point where it intersects the x-axis. In other terms, it can also be called x-intercepts of the graph of the function.
To find the value of the zero for the given function, set the function equal to zero and then calculate the value of the variable of the function; the corresponding values are called Zeros. To further simplify the concept, Zero of the function is defined as the point where the function becomes zero or crosses the x-axis of the graph of a function.
Another important thing to consider is that a function can have more than one zero depending upon the degree of the polynomial or function. A degree of function is defined as the highest degree of its variable. Therefore, the total number of zeros of any function depends upon the degree of the function.
For instance, to further clarify this concept, a Linear function is a degree 1 function. Hence, all the linear functions have only one zero. Similarly, a Quadratic function is a second-degree function, therefore all the quadratic functions have two zeros or it intersects the x-axis of the graph of a function at two points.
What Is a Real Zero?
A zero is said to be a Real zero if it belongs to the set of a real number provided that the function of value becomes zero. If f(x) = 0 where x $\in$ $\mathbb{R}$, then x is called a real zero of the function.
What Is the Difference Between Zero and Root?
The main difference between zero and root is that zero is associated with a function whereas a root refers to an equation. A zero of a function is a value at which the function becomes zero as x is referred to as a root of the function f(x) if and only if the f(x) becomes equal to zero.
A root of an equation is the value of its variable x at which the equation is satisfied or both sides of the equation become equal. A polynomial equation can also have more than one root depending upon the degree of the polynomial equation.
Features of a Zeros Calculator
A Zeros Calculator is a very useful tool as it not only provides you with the roots of the function, but it also has some additional features listed below:
Figure-2 Features of Zeros
Root Plot
A root plot is a graphical representation of all the roots of the function. It shows the graph of a function with the indication of x-intercepts that are the zeros of the function.
Number Line Representation
The zeros calculator also represents the zeros of the function on the number line. A number line is defined as the line on which various points are marked at various intervals.
Sum of Roots
The zeros calculator also provides the sum of all the roots of the function.
Product of Roots
Lastly, it also calculates the product of all the roots of the function.
Solved Examples
Example 1:
Find the roots of the given function using the Zeros Calculator. Draw the root plot and number line representation of the zeros. Also, find the sum and product of the roots of the function.
\[ f(x) = x^2-8 \]
Enter the given function in the expression tab of the Zeros Calculator.
It will display the following results:
The roots of the function are given as:
\[ x = + 2 \sqrt{2} \]
\[ x = – 2 \sqrt{2} \]
The root plot is shown in Figure 1:
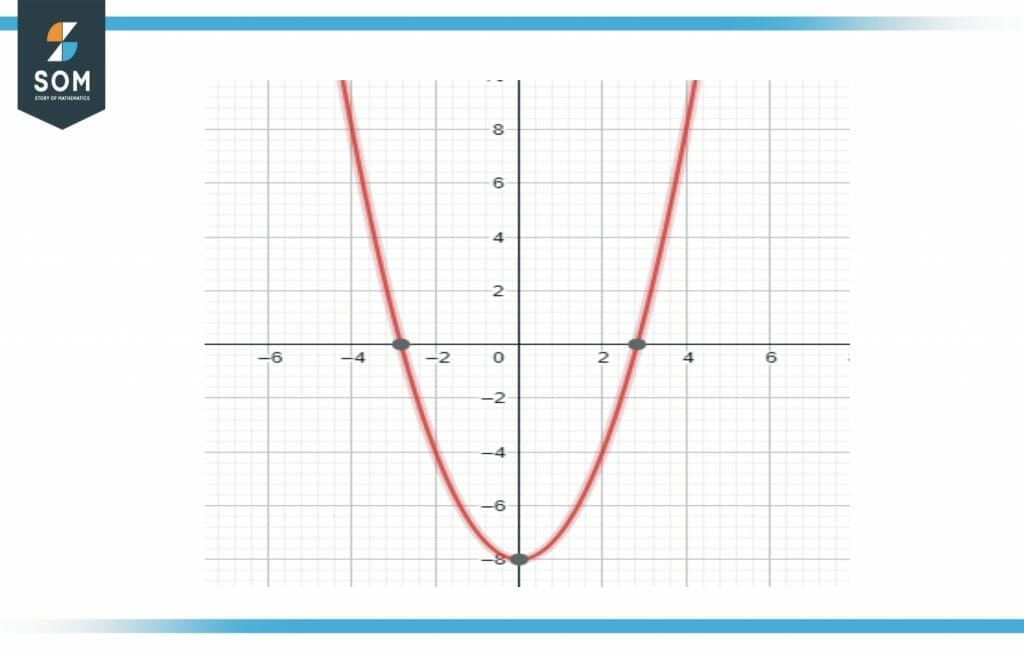
Figure 3 Zeros of function three
Zeros represented on Number Line are shown in Figure 2:
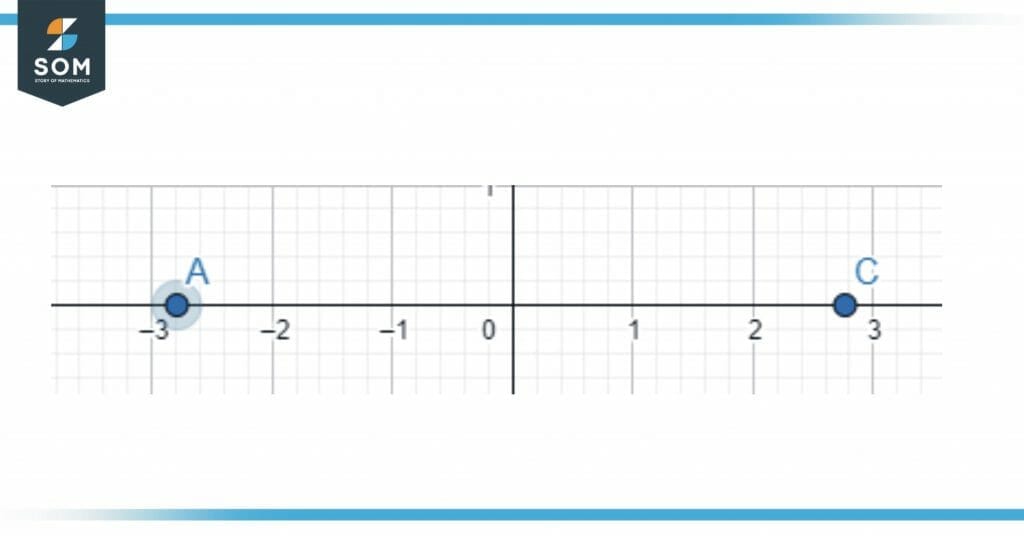
Figure 4 Zeros of function four
The sum of all the roots:
sum = 0
product = – 8
Example 2:
Find the zeros of the following trigonometric function:
\[ f(x) = 2 sin x + \sqrt{3} \]
Use the calculator to find the roots.
Enter the given function in the expression tab of the Zeros Calculator to find the zeros of the function.
It will display the following results:
The roots of the function are given as:
\[ x = \dfrac{2}{3} \pi ( 3n + 2) \]
\[ x = \dfrac{1}{3} \pi ( 6n – 1) \]
Example 3:
Find the zeros of the following function given as:
\[ f(x) = x^4 – 16 \]
Enter the given function in the expression tab of the Zeros Calculator to find the zeros of the function.
This polynomial function has 4 roots (zeros) as it is a 4-degree function. It has two real roots and two complex roots
It will display the results in a new window.
The roots of the function are given as:
x = + 2
x = – 2
x = + 2i
x = – 2i
Example 4:
Find the zeros of the following polynomial function:
\[ f(x) = x^4 – 4x^2 + 8x + 35 \]
Use the calculator to find the roots.
Enter the given function in the expression tab of the Zeros Calculator to find the zeros of the function.
This is a polynomial function of degree 4. Therefore, it has four roots.
All the roots lie in the complex plane.
The roots of the function are given as:
x = -2 – i
x = -2 + i
\[ x = 2 – \iota \sqrt{3} \]
\[ x = 2 + \iota\ \sqrt{3} \]
Previous < Math Calculator List > Next
All, the images are created using Geogebr
