JUMP TO TOPIC
Parabola Calculator + Online Solver With Free Steps
The Parabola Calculator computes various properties of a parabola (focus, vertex, etc.) and plots it given an equation of a parabola as input. A parabola is visually a U-shaped, mirror-symmetrical open plane curve.
The calculator supports 2D parabolas with an axis of symmetry along the x or y-axis. It is not intended for generalized parabolas and will not work for 3D parabolic shapes (not parabolas) such as parabolic cylinders or paraboloids. If your equation is of the form $z = \frac{x^2}{a} + \frac{y^2}{b}$ and the like, the calculator will not work for it.

What Is the Parabola Calculator?
The Parabola Calculator is an online tool that uses the equation of a parabola to describe its properties: focus, focal parameter, vertex, directrix, eccentricity, and semi-axis length. Additionally, it draws the parabola’s plots as well.
The calculator interface consists of a single text box labeled “Enter the equation of the parabola.” It is self-explanatory; you just enter the equation of the parabola here. It could be in any form as long as it depicts a parabola in two dimensions.
How To Use the Parabola Calculator?
You can use the Parabola Calculator to determine the various properties of a parabola and visualize it by simply entering the equation of that parabola into the text box. For example, suppose you want to determine the properties of the parabola described by the equation:
\[ y = x^2 + 4x + 4 \]
The step-by-step guidelines to do so with the calculator follow.
Step 1
Ensure the equation represents a parabola in 2D. It could be in the standard form or even in the form of a quadratic equation. In our case, it is a quadratic equation.
Step 2
Enter the equation into the text box. For our example, we type “x^2+4x+4”. You can also use mathematical constants and standard functions here, such as absolute, by typing “abs,” $\pi$ with “pi,” etc.
Step 3
Press the Submit button to get the results.
Results
The results show up in a new pop-up window that contains three sections:
- Input: The input equation as the calculator understands it in LaTeX format. You can use it to verify that the calculator correctly interpreted the input equation or if there was any mistake.
- Geometric Figure: The type of geometry described by the equation. If it is a parabola, its properties will also appear here. Otherwise, only the name of the geometry shows up. You also have the option to hide the properties if you want.
- Plots: Two 2D graphs with the parabola drawn. The difference between the plots is the range over the x-axis: the first shows a zoomed-in view for convenient closer inspection, and the second a zoomed-out view to analyze how the parabola opens up eventually.
How Does the Parabola Calculator Work?
The Parabola Calculator works by determining the properties of a parabola by analyzing the equation and rearranging it into the standard form of a parabola. From there, it uses the known equations to find the values of the various properties.
As for plotting, the calculator just solves the provided equation over a range of values of x (if the parabola is y-symmetric) or y (if the parabola is x-symmetric) and displays the results.
Definition
A parabola is a set of points on a plane that depicts an open, mirror-symmetrical, U-shaped plane curve. One can define a parabola in multiple ways, but the two most common are:
- Conic Section: The intersection of a 3D cone with a plane such that the 3D cone is a right-circular conic surface and the plane is parallel to another plane that is tangential to the conical surface. Then, a parabola represents a section of the cone.
- Locus of a Point And Line: This is the more algebraic description. It states that a parabola is a set of points in a plane such that every point is equidistant from a line called the directrix and a point not on the directrix called the focus. Such a set of describable points is called a locus.
Keep the second description in mind for the upcoming sections.
Properties of Parabolas
To better understand how the calculator works, we first need to know about the properties of a parabola in more detail:
- Axis of Symmetry (AoS): The line bisecting the parabola into two symmetrical halves. It passes through the vertex and can be parallel to the x or y-axis in certain conditions.
- Vertex: The highest (if the parabola opens downwards) or the lowest (if the parabola opens upwards) point along the parabola. A more concrete definition is the point where the derivative of the parabola is zero.
- Directrix: The line perpendicular to the axis of symmetry such that any point on the parabola is equidistant from it and the focus point.
- Focus: The point along the axis of symmetry such that any point on the parabola is equidistant from it and the directrix. The focus point does not lie on the parabola or the directrix.
- Semi-axis Length: The distance from the vertex to the focus. Also called the focal length. For parabolas, this is equal to the distance from the vertex to the directrix. Therefore, the semi-axis length is half the value of the focal parameter. Notated with $f = \frac{p}{2}$.
- Focal Parameter: The distance from the focus and the corresponding directrix. Sometimes also called the semi-latus rectum. For parabolas, this is double the semi-axis/focal length. Notated as p = 2f.
- Eccentricity: The ratio of the distance between the vertex and focus to the distance between the vertex and directrix. It determines the type of conic (hyperbola, ellipse, parabola, etc.). For a parabola, eccentricity e = 1, always.
Equations of Parabolas
Multiple equations describe parabolas. However, the easiest ones to interpret are the standard forms:
\[ y = a(x-h)^2 + k \tag*{(y-symmetric standard)} \]
\[ x = a(y-k)^2 + h \tag*{(x-symmetric standard)} \]
Quadratic equations also define parabolas:
\[ y = ax^2 + bx + c \tag*{(y-symmetric quadratic)} \]
\[ x = ay^2 +by + c \tag*{(x-symmetric quadratic) } \]
Evaluating Parabola Properties
Considering the equation:
\[ y = a(x-h)^2 + k \]
The axis of symmetry (AoS) for a parabola described in the standard form is parallel to the axis of the non-square term in the equation. In the above case, this is the y-axis. We will find an exact equation of the line once we have the vertex.
The direction in which the parabola opens is towards the positive end of the AoS if a > 0. If a < 0, the parabola opens towards the negative end of the AoS.
The values of h and k define the vertex. If you rearrange the equation:
\[ y-k = a(x-h)^2 \]
You can see that h and k represent offsets along the x and y-axis. When both are zero, the vertex is at (0, 0). Otherwise, it is at (h, k). As the AoS passes through the vertex and we know it is parallel to either the x or y-axis, we can say that AoS: y=k for x-symmetric and AoS: x=h for y-symmetric parabolas.
The semi-axis length is given by $f = \frac{1}{4a}$. The focal parameter is then p = 2f. The focus F and directrix D values depend on the axis of symmetry and the direction in which the parabola opens. For a parabola with vertex (h. k):
\[ F = \left\{ \begin{array}{rl} \text{x-symmetric :} & \left\{ \begin{array}{rcl} (h-f,\, k) & \text{for} & a < 0 \\ (h + f,\, k) & \text{for} & a > 0 \end{array} \right. \\ \text{y-symmetric :} & \left\{ \begin{array}{rcl} (h,\, k-f) & \text{for} & a < 0 \\ (h,\, k+f) & \text{for} & a > 0 \end{array} \right. \end{array} \right. \]
\[ D = \left\{ \begin{array}{rl} \text{x-symmetric :} & \left\{ \begin{array}{rcl} y=h+f & \text{for} & a < 0 \\ y = h-f & \text{for} & a > 0 \end{array} \right. \\ \text{y-symmetric :} & \left\{ \begin{array}{rcl} x=k+f & \text{for} & a < 0 \\ x=k-f & \text{for} & a > 0 \end{array} \right. \end{array} \right. \]
Solved Examples
Example 1
Consider the quadratic equation:
\[ f(x) = \frac{1}{4}x^2 + 15x + 220 \]
Given that quadratic functions represent a parabola – find the focus, directrix, and the length of the semi-latus rectum for f(x).
Solution
First, we bring the function into the standard form of a parabola equation. Putting f(x) = y and completing the square:
\[ y = \frac{1}{4}x^2+15x+225-5 \]
\[ y = \left( \frac{1}{2}x \right)^2 + 2 \left( \frac{1}{2} \right) \left( 15 \right)x + 15^2-5 \]
\[ y = \left( \frac{1}{2}x + 15 \right)^2-5 \]
\[ y = \frac{1}{4} \left(x + 30 \right)^2-5 \]
Now that we have the standard form, we can find the properties easily by comparing:
\[ y = a(x-h)^2 + k \]
\[ \Rightarrow a > 0 = \frac{1}{4}, h= -30, k = -5 \]
\[ \text{vertex} = (h, k) = (-30, -5) \]
The axis of symmetry is parallel to the y-axis. Since a > 0, the parabola opens upwards. The semi-axis/focal length is:
\[ f = \frac{1}{4a} = 1 \]
\[ \text{Focus :} \,\, (-30,\, -5+f) = \mathbf{(-30,\, 4)} \]
The directrix is perpendicular to the AoS and hence a horizontal line:
\[ \text{Directrix :} \,\, y = -5-f = \mathbf{-6} \]
The length of the semi-latus rectum equals the focal parameter:
\[ \text{Focal Param :} \,\, p = 2f = \mathbf{2} \]
You can visually verify the results in Figure 1 below.
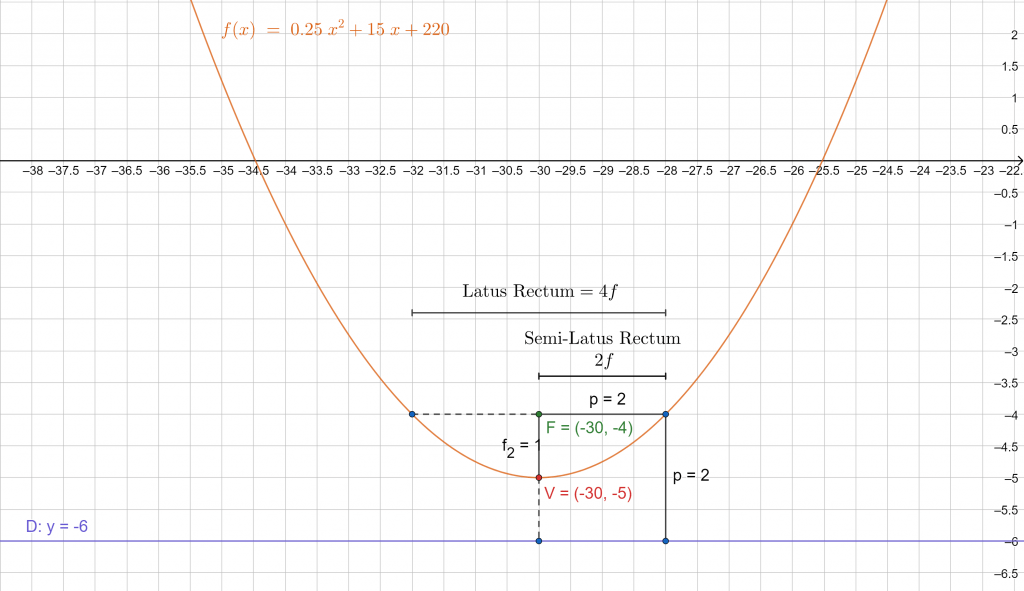
Figure 1
All graphs/images were created with GeoGebra.
