JUMP TO TOPIC
Projectile Motion Calculator + Online Solver With Free Steps
The online Projectile Motion Calculator is a calculator that calculates the time and distance an object moves when thrown.
The Projectile Motion Calculator is a powerful tool used by physicists that helps them quickly find and graph the results of a moving projectile.

What Is a Projectile Motion Calculator?
A Projectile Motion Calculator is an online calculator that finds the motion of a projectile given its velocity and angle.
The Projectile Motion Calculator requires two inputs; the initial velocity of the projectile and the degree at which the projectile is thrown.
After inputting the values in the Projectile Motion Calculator, the calculator finds the projectile’s motion.
How To Use a Projectile Motion Calculator?
To use the Projectile Motion Calculator, you input the required values in the calculator and click the “Submit” button.
The detailed instructions on using the Projectile Motion Calculator are given below:
Step 1
First, we enter the projectile’s initial velocity into the Projectile Motion Calculator.
Step 2
After entering the projectile’s initial velocity, we add the angle at which the object is thrown in the Projectile Motion Calculator.
Step 3
Finally, after adding both the input values in the Projectile Motion Calculator, we click the “Submit” button. This quickly displays the results and plots a graph for the projectile’s motion.
How Does a Projectile Motion Calculator Work?
The Projectile Motion Calculator works by taking in the inputs and applying different formulas to it, which allows the calculator to derive the horizontal distance traveled, the maximum height of the projectile, and the time taken for the projectile to reach its destination.
Here are the different formulas used by the Projectile Motion Calculator:
\[ h = \frac{y^{2}\sin^{2}{(2\alpha)}}{2g}, \]
Where, h = maximum height of the projectile
\[ x = \frac{y^{2}\sin{(2\alpha)}}{g}\]
Where, x = horizontal distance traveled by the projectile
\[ T = \frac{2y\sin{(\alpha)}}{g} \]
Where, T = time traveled by the projectile
What Is a Projectile?
A projectile is an object in which gravity is the only force at work. Projectiles come in a variety of examples. A projectile is an object launched from rest (provided that the influence of air resistance is negligible).
A projectile is something that is thrown straight up in the air and is also anything hurled upward at an angle to the horizontal. A projectile is any object that, after being launched or dropped, continues to move due to its inertia and is only affected by the downward gravitational force.
The force of gravity is the only force that can be said to act on a projectile. An object wouldn’t be a projectile if another force exerted itself on it. An object travels along a route known as the trajectory after being launched.
Projectile Motion
Projectile motion, which simply depends on the beginning velocity, the launch angle, and the acceleration due to gravity, characterizes the projectile’s trajectory.
The speed an object is moving at when it is initially launched into the air is known as its initial speed or velocity. The angle at which an object is launched is referred to as the launch angle.
An object’s maximum height, range, and flight time depend on its speed and curve when it leaves the launchpad. It is significant to remember that, under the assumption of negligible air resistance, an object launched into the air is simply affected by the force of gravity.
An object moving in a projectile motion will follow a predictable path. Only the initial circumstances (launch angle, initial velocity, and acceleration due to gravity) determine the object’s parabolic course.
The maximum height and range of the projectile will fluctuate as the initial velocity or launch angle changes. A higher beginning velocity will produce a larger size and coverage.
The maximum height and range are affected differently by increasing the launch angle. The angle that makes the most significant range is probably not the one that produces the most significant maximum height.
The predictable trajectory has led to the formulation of kinematic equations that relate to the essential elements of projectile motion. These motion equations describe the projectile’s starting and terminal velocities, as well as its displacement, time of flight, and acceleration. They can be used to calculate these variables provided the appropriate information is known.
If the initial velocity, acceleration, and duration of flight are known, the final velocity can be computed using the following equation:
v = u +at
Here, u is the initial velocity, t is the time, and a is the projectile’s acceleration.
The initial velocity, acceleration, and time of flight can also be used to determine the displacement according to the following formula:
\[ s = ut + \frac{1}{2}at^{2} \]
The final velocity can be computed using this displacement if only the displacement is provided and not the flight time, by using the following formula:
\[ v^{2}=u^{2}+2as \]
Solved Examples
The Projectile Motion Calculator instantly calculates the projectile motion of an object. Here are some examples solved using the Projectile Motion Calculator.
Example 1
A football player kicks a football at a speed of 20 (meters per second) with an angle of 45(degrees). Using the Projectile Motion Calculator, find the horizontal distance, time traveled, and the maximum height of the football.
Solution
We can quickly find the football’s motion using the Projectile Motion Calculator. First, we input the initial velocity of the football into the Projectile Motion Calculator; the initial velocity is 20 (meters per second). After adding the initial velocity, we add the angle at which the football is kicked; the angle is 45(degrees).
After adding both inputs to our Projectile Motion Calculator, we click the “Submit” button. The Projectile Motion Calculator quickly displays the results and plots a graph for the football’s trajectory.
The following results are extracted from the Projectile Motion Calculator:
Input Information:
Projectile Path:
initial speed = 20 (meter per second)
release angle relative to horizontal = 45(degrees)
Results:
Travel Time = 2.88 seconds
Maximum Height = 10.2 meter = 33.46 feet
Horizontal distance traveled = horizontal distance traveled = 40.79 meters = 133.8 feet
Equation:
\[ h = \frac{y^{2}\sin^{2}{(2\alpha)}}{2g}, \]
\[ x = \frac{y^{2}\sin{(2\alpha)}}{g} \]
\[ T = \frac{2y\sin{(\alpha)}}{g} \]
T = travel time
v = initial speed
$\alpha$ = release angle relative to horizontal
h = maximum height
x = horizontal distance traveled
g = standard acceleration due to gravity of earth ($\approx$ 9.807 $\frac{m}{sec^{2}}$)
Projectile Path:
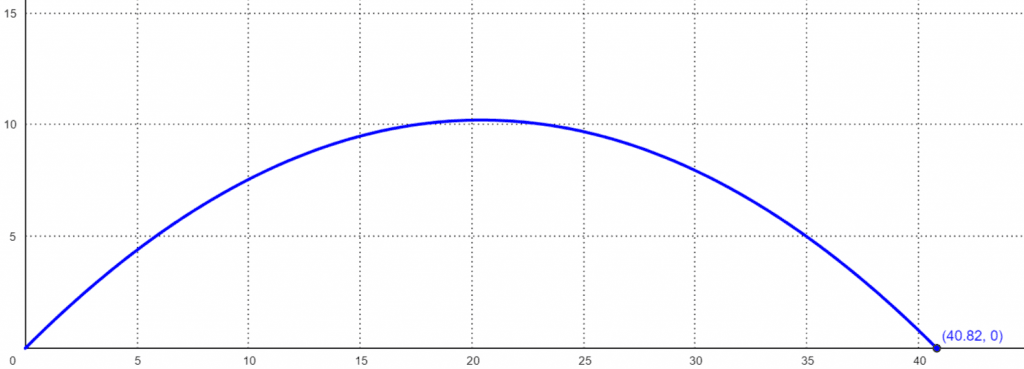
Figure 1
Example 2
A student is given the following values:
Initial velocity = 30 (meter per sec)
angle = 60 (degrees)
Use the equations to find the projectile motion.
Solution
We can use the Projectile Motion Calculator to solve this equation. First, we plug the initial velocity and the angle into the calculator. We then click the “Submit” button, which displays the result and plots the graph of the projectile.
The following results are taken from the Projectile Motion Calculator:
Input Information:
Projectile Path:
Initial speed = 30 (meter per second)
Release angle relative to horizontal = 60 (degrees)
Results:
Travel time = 5.299 seconds
Maximum height = 34.42 meter = 112.9 feet
Horizontal distance traveled = horizontal distance traveled = 79.48 meters = 260.8 feet
Equation:
\[ h = \frac{y^{2}\sin^{2}{(2\alpha)}}{2g}, \]
\[ x = \frac{y^{2}\sin{(2\alpha)}}{g} \]
\[ T = \frac{2y\sin{(\alpha)}}{g} \]
T = Travel time
v = initial speed
$\alpha$ = release angle relative to horizontal
h = maximum height
x = horizontal distance traveled
g = standard acceleration due to gravity of earth ($\approx$ 9.807 $\frac{m}{sec^{2}}$)
Projectile Path:
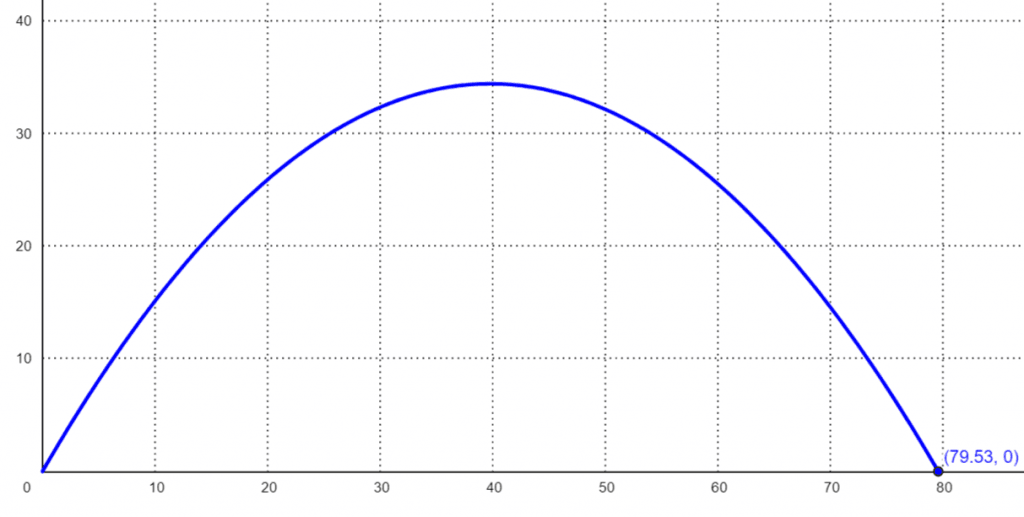
Figure 2
All images/graphs are created using GeoGebra
