JUMP TO TOPIC
Partial Derivative Calculator + Online Solver With Free Steps
A Partial Derivative Calculator is used to calculate a given function’s partial derivatives. Partial derivatives are much like the normal derivatives, but these are specific to problems involving more than one independent variable.
When differentiating a function for one variable, everything not associated with the variable is considered a constant and treated as such. This, therefore, does not change even when dealing with partial differentiation.

What Is a Partial Derivative Calculator?
A Partial Derivative Calculator is a calculator that is used to solve your partial differentiation problems right here in your browser. You can run this calculator online and solve as many problems as you like. The calculator is very simple to use and is designed to be extremely intuitive and straightforward.

Figure 1 Partial Derivative Formula
Partial differentiation is a partial derivative calculator that takes place for a function expressed by more than one independent variable. When solving for one of these variables, the rest are considered constants.
How To Use a Partial Derivative Calculator?
You can start using this calculator by first entering the given functions then selecting the variables you want to differentiate against. The Partial Derivative Calculator can easily be used following the steps given below.
To use this calculator, you must first have a problem involving a multivariable function and have a variable of choice for which you want to calculate the partial derivative.
Step 1:
You start by entering the given function with its variables expressed in terms of x, y, and z.
Step 2:
This step is followed by a selection of the variable you would like to differentiate your given function of x, y, and z against.
Step 3:
Then, you simply press the button labelled “Submit” to get your calculated results. Your result will show in the space given below the input boxes of the calculator.
Step 4:
Finally, to use the calculator again you can simply change the entries in the input boxes and keep solving as many problems as you want.
It is important to note that this calculator only works for as many as three independent variables. Therefore, for problems involving more than three variables this calculator would not be very effective.
How Does the Partial Derivative Calculator Work?
The Partial Derivative Calculator works by applying differentiation on the given function separately for each variable in question. A standard differential d is applied to a simple equation involving only one independent variable.
Differentiation
Differentiation is described as the act of finding a difference, as differentiation of a time signal is interpreted as the change in time i.e., the difference in time. Differentiation is used heavily in the field of engineering and mathematics under the subject of calculus.
Calculus, therefore, research change to build a bridge between the physical and the theoretical world of science. So a difference in the distance with respect to time in physics as well as mathematics would result in a value called speed, where speed is defined as the change in distance in a given amount of time.
\[v = \frac{ds}{dt}\]
Differential
A differential is always applied to an expression for a variable, and the derivative of any expression is therefore taken by applying a differential concerning the variable the expression depends upon.
Thus, for an expression given as:
\[y = 2x^2 + 3\]
The derivative would look like this:
\[ \frac{dy}{dx} = 2 \frac{dx^2}{dx} + 3 \frac{d}{dx} = 2 \times 2 x = 4x\]
Partial Differential
A partial differential as described above is used for equations relying on more than one variable. This complicates matters a lot as now, there is no one variable to differentiate the whole expression with.
Therefore, under such circumstances, the best course of action is to break the differential into as many pieces as variables in the given function. Thus, we begin to differentiate the expression partially. The partial derivative for a function is denoted by a squiggly d, “$\partial$”.
Now take the following equation as a test function:
\[ a = 3x^2 + 2y – 1\]
Applying partial derivative with respect to x would result into:
\[ \frac {\partial a}{\partial x} = 3\frac {\partial x^2}{\partial x} + 2\frac {\partial y}{\partial x} – 1\frac {\partial }{\partial x} = (3 \times 2)x + 0 – 0 = 6x \]
Whereas if you were to solve for y, then the result would become:
\[ \frac {\partial a}{\partial y} = 3\frac {\partial x^2}{\partial y} + 2\frac {\partial y}{\partial y} – 1\frac {\partial }{\partial y} = (3 \times 0) + 2 – 0 = 2 \]
So, when you are solving for any one variable out of the many given in your function, the one for which you are differentiating is the only one used. The rest of the variables behave like constants and can be differentiated to zero as there is no change in a constant value.
History of Partial Derivative
The partial Derivatives symbol was first used in the 1770s by the renowned French mathematician and philosopher Marquis de Condorcet. He had used the symbol expressed as $\partial$ for partial differences.
The notation being used to this day for partial derivatives was then introduced in 1786 by Adrien-Marie Legendre. Although this notation did not become popular until as late as 1841 when the German mathematician Carl Gustav Jacob Jacobi normalized it.
The inception of the partial differential equations occurred during the golden year of 1693. This was the year in which Leibniz discovered a way to solve a differential equation and Newton brought forth the publication of these equations’ older solution methods.
Solved Examples
Example 1
Consider the given function $f(x, y) = 3x^5 + 2y^2 – 1$, solve for partial derivatives with respect to both x, and y.
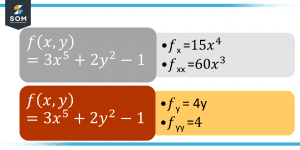
Figure 3 Partial Derivatives of given function with respect to x and y
First, we express the following expression in terms of partial derivative of f(x, y) with respect to x, given as fx.
\[f_x = 3\frac {\partial x^5}{\partial x} + 2\frac {\partial y^2}{\partial x} – 1\frac {\partial}{\partial x}\]
Now solving the differentials results in the following expression representing a partial derivative with respect to $x$:
\[f_x = (3 \times 5)x^4+ (2 \times 0) – (1 \times 0) = 15x^4\]
Following the x derivative, we solve for the partial differential of f(x, y) with respect to y. This results in the following expression, given as fy.
\[f_y = 3\frac {\partial x^5}{\partial y} + 2\frac {\partial y^2}{\partial y} – 1\frac {\partial}{\partial y}\]
Solving this partial derivative problem would result into the following expression:
fx = (3 x 0)+ (2 x 2)y – (1 x 0) = 4y
Hence, we can compile our results as follows:
\[f_x = 15x^4, f_y = 4y \]
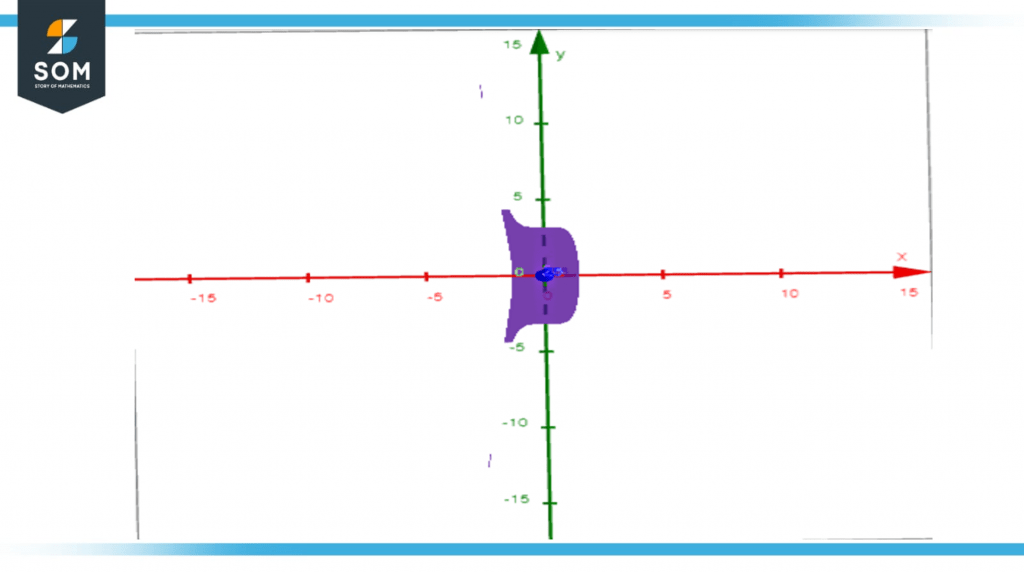
Figure-3 Graph of f(x, y) = 3x^5 + 2y^2 – 1
Example 2
Consider the given function $f(x, y, z) = 2x^2+y+5z^3-3$, solve for partial derivatives with respect to x, y, as well as z.
First, we express the following expression in terms of partial derivative of f(x, y, z) with respect to $x$, given as fx.
\[f_x = 2\frac {\partial x^2}{\partial x} + \frac {\partial y}{\partial x} + 5\frac {\partial z^3}{\partial x} – 3\frac {\partial}{\partial x}\]
Now solving the differentials results in the following expression representing a partial derivative with respect to $x$:
fx = (2 x 2)x+ (1 x 0) + (5 x 0) – (3 x 0) = 4x
Following the x derivative, we solve the partial differential with respect to y therefore producing a result expressed as fy.
\[f_y = 2\frac {\partial x^2}{\partial y} + \frac {\partial y}{\partial y} + 5\frac {\partial z^3}{\partial y} – 3\frac {\partial}{\partial y}\]
Solving this partial derivative problem would result into the following expression:
fy = (2 x 0)+ 1 + (5 x 0) – (3 x 0) = 1
Finally, we solve f(x, y, z) for z.
\[f_z = 2\frac {\partial x^2}{\partial z} + \frac {\partial y}{\partial z} + 5\frac {\partial z^3}{\partial z} – 3\frac {\partial}{\partial z}\]
Solving the partial differentials results into:
\[f_z = (2 \times 0)+ (1 \times 0) + (5 \times 3)z^2 – (3 \times 0) = 15z^2\]
Hence, we can compile our results as follows:
fx = 4x, fy = 1, fz = $15z^2$
Example 3:
Consider the given function $f(x, y, z) = 4x+y^3+2z^2+6$, solve for partial derivatives with respect to x, y, as well as z.
First, we express the following expression in terms of partial derivative of f(x, y, z) with respect to x, given as fx.
\[f_x = 4\frac {\partial x}{\partial x} + \frac {\partial y^3}{\partial x} + 2\frac {\partial z^2}{\partial x} + 6\frac {\partial}{\partial x}\]
Now solving the differentials results in the following expression representing a partial derivative with respect to x:
fx = 4 + (1 x 0) + (2 x 0) + (6 x 0) = 4
Following the x derivative, we solve the partial differential with respect to y therefore producing a result expressed as fy.
\[f_y = 4\frac {\partial x}{\partial y} + \frac {\partial y^3}{\partial y} + 2\frac {\partial z^2}{\partial y} + 6\frac {\partial}{\partial y}\]
Solving this partial derivative problem would result into the following expression:
\[f_y = (4 \times 0)+ (1 \times 3)y^2 + (2 \times 0) + (6 \times 0) = 3y^2\]
Finally, we solve f(x, y, z) for z.
\[f_z = 4\frac {\partial x}{\partial z} + \frac {\partial y^3}{\partial z} + 2\frac {\partial z^2}{\partial z} + 6\frac {\partial}{\partial z}\]
Solving the partial differentials results into:
fz = (4 x 0)+ (1 x 0) + (2 x 2)z + (6 x 0) = 4z
Hence, we can compile our results as follows:
fx = 4, fy = $3y^2$, fz = 4z
