JUMP TO TOPIC
Cylindrical Coordinates Integral + Online Solver With Free Steps
A Cylindrical Coordinates Calculator acts as a converter that helps you solve functions involving cylindrical coordinates in terms of a triple integral.

Such a calculator works on the provision of cylindrical coordinates parameters and utilizes them for the solution of triple integrals. One thing to note about cylindrical coordinates triple integrals is that they are written as shown below:
\[ \iiint_{V} f dV \]
Or you can even write it as:
\[\iiint_{V} f dV = \int^{\beta}_{\alpha} \int^{r_{2}}_{r_{1}} \int^{z_{2}}_{z_{1}} r f z dz dr d\theta \]

Figure 1 Labelled Diagram for Cylindrical coordinates
What Is a Cylindrical Coordinate Integral Calculator?
The Cylindrical Triple Integral Calculator is a calculator that plays an immense role in solving geometry-related questions, specifically about cylindrical figures. For efficient functioning of the triple integral calculator, you need to have the correct values of the cylindrical coordinates.
If you have those already, simply input those values and your function. The answer to your question will be just one step away. You can even view the graphical representation of some of the functions.
Using this calculator not only saves your time but also keeps you away from problem-solving troubles. The calculator can support integrating functions involving cylindrical variables and you can also use it to check your answers.
Another feature is that you can obtain your answers in fewer as well as more digits, whichever suits your requirement.
How To Use a Cylindrical Coordinate Integral Calculator
A Cylindrical Integral Coordinate calculator is very easy-to-use. There are a few very basic steps to use the calculator and get the answer to your questions.
The important thing is to have all the inputs before you start working. You may proceed with solving your question using the cylindrical coordinates integral calculator by following the steps mentioned below:
Step 1:
Consider your function and analyze the cylindrical variables.
Step 2:
Before you start putting in values, make sure your concept regarding cylindrical coordinates and triple integrals is clear. Type in your function and put in the values of the parameters of the cylindrical coordinate.
Step 3:
It is recommended to do the steps one by one and not all together to avoid confusion.
Once you are done putting in values in the triple integral calculator, press the button that says “Submit” at the bottom of the calculator and you will get your answer.
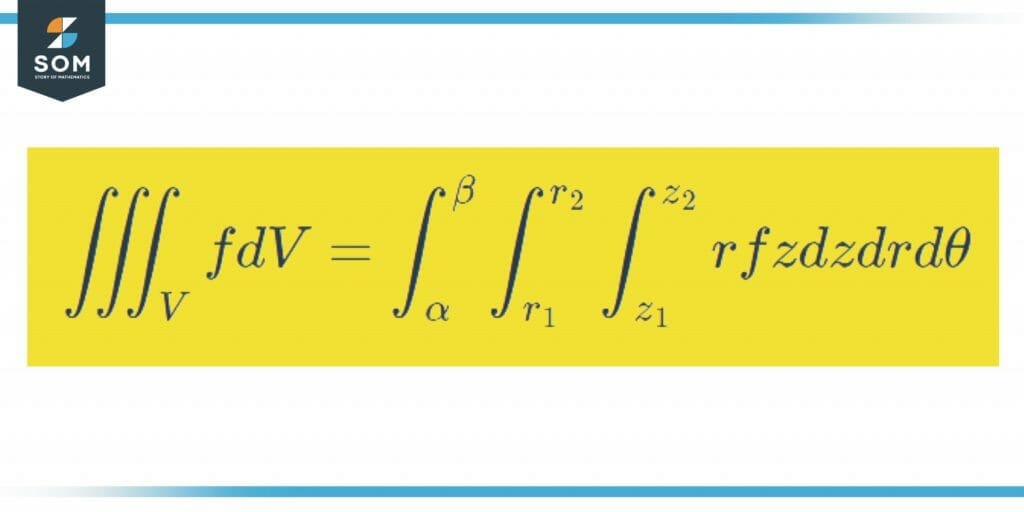
Figure 2 Formula to calculate the cylindrical coordinates
How Does a Cylindrical Coordinates Integral Calculator Work?
A Cylindrical Coordinate Integral Calculator works by computing the triple integral of the given function in the specified domain.
Let’s have a detailed overview of some important concepts.
What Is a Cylindrical Coordinates System?
A cylindrical coordinate system is an extended polar system, which means that it adds up the third axis to the polar system to create a 3-dimensional system. This system of 3 coordinates is known as a cylindrical coordinate system.
The three parameters or coordinates of a cylindrical coordinate system, about any point within the system, are given below:
- Radial distance r from the z-axis to the point.
- Height of z depicts the distance from the plane you choose to the point.
- $\theta$ is an angle between directions given as reference on the plane chosen. It is also the angle on the line from the origin to the projection of the point.
What Are Cylindrical Coordinates?
Cylindrical coordinates are the coordinates created when we add up the third axis to form a three-dimensional polar system. Defined shortly, it is the extension of a two-dimensional system to a three-dimensional system by adding up an axis.
An interesting fact about the cylindrical coordinates is that they are used to specify the positions of stars in the galaxy. In cartesian coordinates, the dV in the formula represents a tiny unit of volume and it is expanded as:
dV = dz dr d$\theta$
You can simply add up all the small volumes and find the volume of the three-dimensional regions with great ease.
What Is the Difference Between Cylindrical and Spherical Coordinates?
The main difference between the Spherical and Cylindrical Coordinates is based on the location of the point, as the location of a point is determined using two distances e.g. y and z, and an angle measure i.e. $/theta$ in the cylindrical coordinate system. However, in the spherical coordinate system, an ordered triple is used to describe the location of a point.
Another clear difference is that a spherical coordinate system is a two-dimensional system and the cylindrical coordinate system is three-dimensional.
In addition to this, if you set your height constant in cylindrical coordinates, you get the polar coordinates, but spherical coordinates are obtained by setting the height in a polar angle constant, also known as azimuth angle.
Solved Examples
Example 1:
Evaluate the triple integral given below:
\[ \iiint_{R} (zr sin\theta) r dz dr d\theta \]
Where,\[ R = {(z, r, \theta) | 0\leqslant z\leqslant 3, 1\leqslant r \leqslant 2, 0\leqslant \theta \leqslant \pi} \]
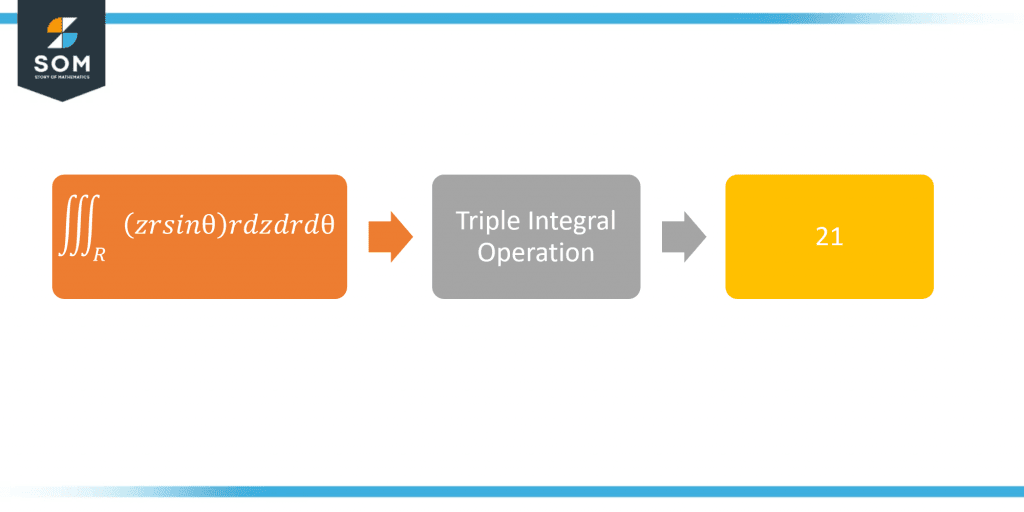
figure 3 Tripple integral solved example
Solution:
For the given integral, the parameters of the cylindrical coordinates are already given. Inserting them in the integral gives us the following equation:
\[ \iiint_{R} (zr sin\theta) r dz dr d\theta = \int^{\pi}_{0} \int^{2}_{1} \int^{3}_{0}(zr sin\theta) r dz dr d\theta\]
Now, each variable will be integrated independently from the others. Integrating each variable separately gives us the following equation:
\[ \iiint_{R} (zr sin\theta) r dz dr d\theta = (\int^{\pi}_{0} sin\theta d\theta) (\int^{2}_{1} r^{2} dr) (\int^{3}_{0}z dz) \]
Integrating these variables separately and inserting the values of the parameters in the calculator gives us the following result:
\[ \iiint_{R} (zr sin\theta) r dz dr d\theta = 21\]
Example 2:
Evaluate the triple integral for which the function f and the cylindrical coordinates are given below:
\[ f = r^{2} + z^{2} \]
The given cylindrical coordinates are:
\[ R = {0 \leqslant z\leqslant \sqrt{16-r^{2}}, 0\leqslant r \leqslant 2 sin\theta, 0\leqslant \theta \leqslant \pi } \]
Solution:
For the given function, the parameters of the cylindrical coordinates are already given. We need to evaluate the triple integral for this function and these coordinates. The triple integral can be written as:
\[ \iiint_{R} (r^{2}+z^{2}) r dz dr d\theta \]
Or:
\[ \iiint_{R} (r^{2}+z^{2}) r dz dr d\theta = \int^{\pi}_{0} \int^{2sin\theta}_{1} \int^{\sqrt{16-r^{2}}}_{0} (r^{2}+z^{2}) r dz dr d\theta \]
Now, each variable will be integrated independently from the others. Integrating these variables separately and inserting the values of the parameters in the calculator gives us the following result:
\[ \iiint_{R} (r^{2}+z^{2}) r dz dr d\theta = 40.3827 \]
