Summation Calculator + Online Solver With Free Steps

The Summation Calculator is a calculator that uses a single variable function with the upper and lower limit of summation. It gives the outputs as the resultant sum by adding the function values. These function values are obtained by placing the sequence in the function and solving it.

The calculator also displays a graph that shows the individual partial sums obtained from the function.

The summation symbol is represented by a Greek capital letter $\Sigma$, known as the sigma notation. It denotes the sum of various terms.

What Is Summation Calculator?

The Summation calculator is a calculator that computes the summation of the given function values by providing the initial and final values of a sequence to it. The starting and ending values for the sequence are entered by the user.

A sequence is a set of numbers that is written in a definite order. The addition of the entities of a particular sequence results in a finite series. This calculator can compute the result of any finite series.

Summation or $\Sigma$ requires an index that varies to enclose all terms to be considered in the sum. The index provides the starting and the ending values for the series. This index is denoted by k written in subscript under the sigma notation. It can also be described by any other variable used in the function.

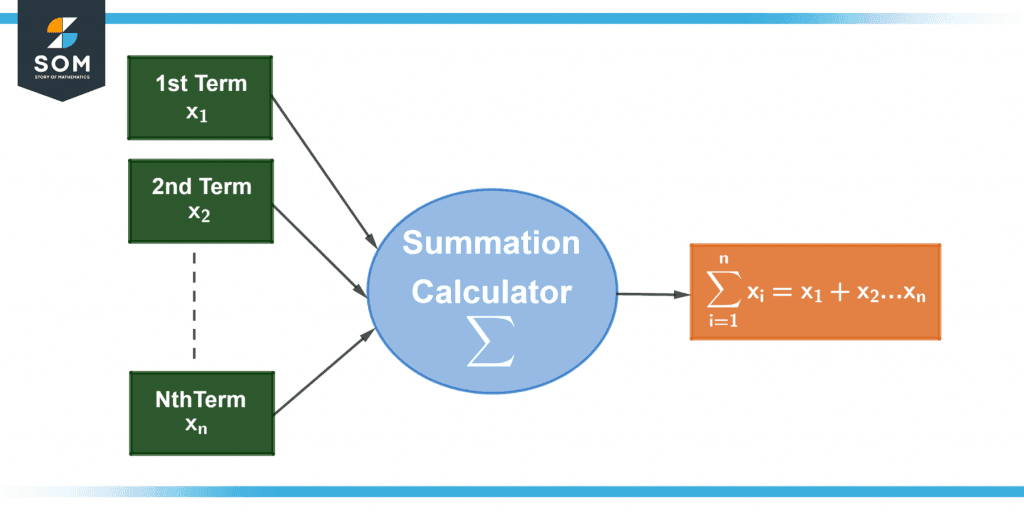
Figure 1: Summation Calculator Function

For instance, in $ \sum_{k=1}^{4} 2k$, the index of summation is $k$, the first value of k is 1, and the last value of k is 4. The function written with the summation is 2k. The values of k from 1 to 4 are placed in the function and the resulting sequence is added simultaneously to give the final sum.

How To Use the Summation Calculator

Using the Summation Calculator is not a difficult job at all. Just follow the simple steps mentioned below and you can compute the sum of any series or a function.

Let’s find out how to use the Summation Calculator:

Step 1:

Enter the function against the block titled Sum of. It can be any function of a single variable (alphabet). The default example shows the simple function k.

Step 2:

In the block titled from, enter the function variable . For example, in the function 2n+1, the variable used is n, so n should be entered.

Step 3:

In the block titled =, enter the starting value of the sequence. This number will determine the first value of the series when put into the given function.

Step 4:

In the last block titled to, enter the ending value of the sequence. This number makes the resulting series finite. This will be the last value placed in the function for the total sum.

Step 5:

Press the submit button to get the final result.

Result

The results will be displayed in two blocks, the Sum and the Partial sums.

Sum

The Sum indicates the final result of the series obtained by putting all the values from the start to the end in the function. It will show the equation including the summation symbol.

Partial Sums

The Partial Sums are the individual sums obtained by putting all the individual values in the function from the lower limit to the upper limit. The result will display a graph with the x-axis as the variable of the function and the y-axis as the sum of functions with varying values of the variable. The blue dots indicate all the partial sums in the total summation.

Solved Examples

Example 1:

For the function $3k^2$

such as the k = 1 to 4.

The summation calculator will calculate the partial sums as follows:

\[ S_{1} = \sum _{k=1} ^{4} { 3(1)^2 } = 3 \]

\[ S_{2} = \sum _{k=1} ^{4} { 3(2) ^2 } = 12 \]

\[ S_{3} = \sum _{k=1} ^{4} { 3(3) ^2 } = 27 \]

\[ S_{4} = \sum _{k=1} ^{4} { 3(4) ^2 } = 48 \]

So the resultant sum will be:

Sk = S1 + S2 + S3 + S4 = 90 

The graph is shown below in Figure 3:

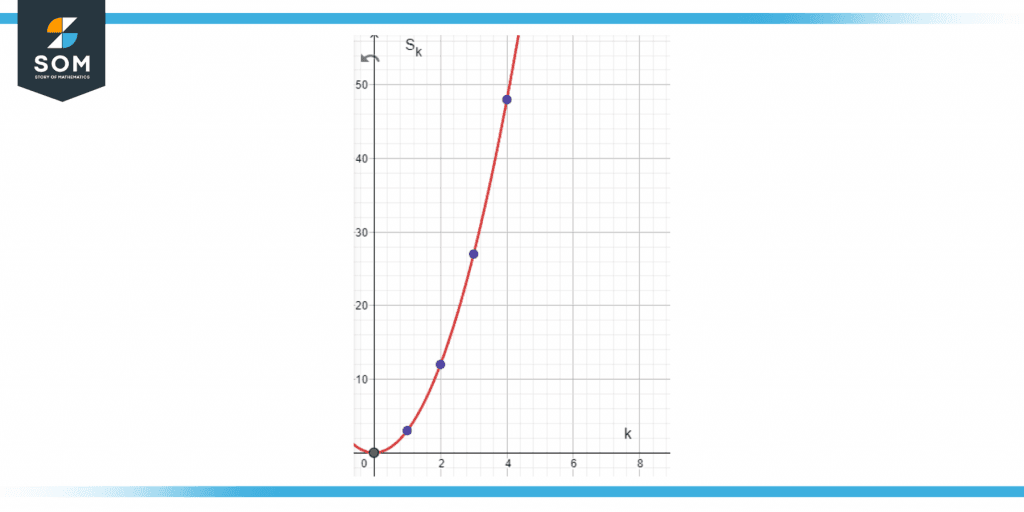
Figure 2: Example Solution

Example 2:

For the function (4n+1)

Where n = 2 to 6. 

Compute the Sum using Summation Calculator.

The summation calculator will compute the partial sums as follows:

\[ S_{2} = \sum _{n=2} ^{6} { 4(2) + 1 } = 9 \]

\[ S_{3} = \sum _{n=2} ^{6} { 4(3) + 1 } = 13 \]

\[ S_{4} = \sum _{n=2} ^{6} { 4(4) + 1 } = 17 \]

\[ S_{5} = \sum _{n=2} ^{6} { 4(5) + 1 } = 21 \]

\[ S_{6} = \sum _{n=2} ^{6} { 4(6) + 1 } = 25 \]

So the final sum will be:

Sn = S2 + S3 + S4 + S5 + S6 = 85 

The graph is shown below in Figure 4:

(x,y) = (2,9) , (3,13) , (4,17) , (5,21) , (6,25)

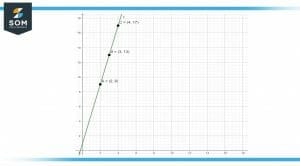
Figure-4 : Graph of function f(4n+1)

Previous < Math Calculator List > Next

All the images are created using Geogebra.