JUMP TO TOPIC
Nth Derivative Calculator + Online Solver With Free Steps
An nth Derivative Calculator is used for calculating the nth derivative of any given function. This type of calculator makes complex differential calculations fairly easy by computing the derivative answer in a matter of seconds.
Nth derivative of a function refers to the differentiation of the function iteratively for n times. It means computing successive derivatives of the specified function for n number of times, where n can be any real number.
The $nth$ derivative is denoted as shown below:
\[ \frac{d^{n}}{dx^{n}} \]

What Is Nth Derivative Calculator?
An nth Derivative Calculator is a calculator that is used for computing the $nth$ derivatives of a function and to calculate the higher-order derivatives.
This calculator takes away the trouble of manually calculating the derivative of any given function for n times.
Often, we encounter certain functions for which the derivative calculations become quite lengthy and complex, even for the first derivative. The nth derivative calculator is the ideal solution for calculating the derivatives for such functions, where $n$ can be 3, 4, and so on.
Taking iterative derivatives of a function assists in predicting the behavior of the function, over time which is of great significance, especially in physics. The $nth$ Derivative Calculators can prove to be quite handy in such situations where the variating behavior of a function needs to be determined.
How To Use the Nth Derivative Calculator
The nth Derivative Calculator is quite simple to use. Apart from its speedy calculations, the best feature of the nth derivative calculator is its user-friendly interface.
This calculator consists of two boxes: one for inputting the number of times the derivative needs to be calculated, i.e, n, and the other for adding the function. A “Submit” button is present just below these boxes, which provides the answer upon clicking.
Given below is a step-by-step guide for using the nth derivative calculator:
Step 1:
Analyze your function and determine the value of n for which you need to calculate the derivative.
Step 2:
Insert the value of n in the first box. The value of n needs to lie in the domain of real numbers. This value corresponds to the number of differential iterations that need to be performed on the function.
Step 3:
In the next box, insert your function f(x). There is no restriction on the type of function that needs to be evaluated.
Step 4:
Once you have entered your value of n and your function, simply click on the button that says “Submit.” After 2-3 seconds, your solved answer will appear in the window below the boxes.
Solved Examples
Example 1:
Calculate the first, second, and third derivative of the function given below:
\[ f(x) = 3x^{4} + 16x^{2} – 3x \]
Solution:

Figure 2 First, second and third derivative
In the given question, we need to calculate the first, second, and third derivatives of the function. So, $n$ = $1$, $2$, and $3$.
Calculating the first derivative:
\[ n = 1\]
\[ f’(x) = \frac{d}{dx} (3x^{4} + 16x^{2} -3x) \]
Upon inserting the value of $n$ and $f(x)$ in the $nth$ derivative calculator, we get the following answer:
\[ f’(x) = 12x^{3} + 32x -3 \]
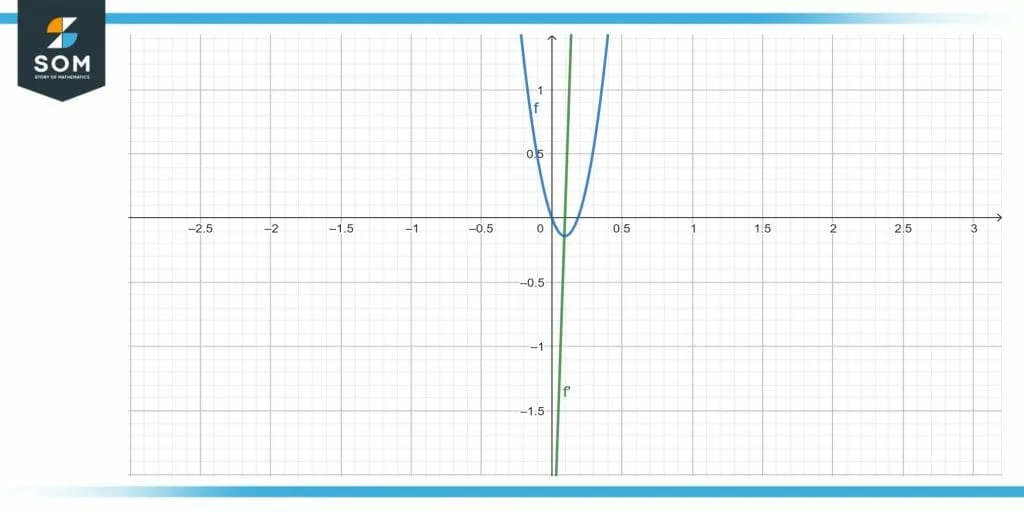
Figure-3 Graph
Now calculate the second derivative:
\[ n = 2 \]
\[ f’’(x) = \frac{d^{2}}{dx^{2}} (3x^{4} + 16x^{2} -3x) \]
Upon inserting the value of $n$ and $f(x)$ in the $nth$ derivative calculator, we get the following answer:
\[ f’’(x) = 4(9x^{2} + 8) \]
Now calculate the third derivative:
\[ n = 3 \]
\[ f’’’(x) = \frac{d^{3}}{dx^{3}} (3x^{4} + 16x^{2} -3x) \]
Upon inserting the value of $n$ and $f(x)$ in the $nth$ derivative calculator, we get the following answer:
\[ f’’’(x) = 72x \]
Example 2:
Find the 7th order derivative of the following function:
\[ f(x) = x. cos(x) \]
Solution:
In the given question, both the value of $n$ and the function $f(x)$ are specified as below:
\[ n = 7 \]
And:
\[ f(x) = x.cos(x) \]
The question demands to calculate the 7th order derivative of this function. For doing so, simply insert the values of $n$ and the function $f(x)$ in the $nth$ derivative calculator. The answer turns out to be:
\[ f^{7} (x) = \frac {d^{7}}{dx^{7}} (x.cos(x)) \]
\[ \frac {d^{7}}{dx^{7}} (x.cos(x)) = x.sin(x) – 7 cos(x) \]
