JUMP TO TOPIC
Least Squares Solution Calculator + Online Solver With Free Steps
A Linear Squares Solution Calculator is used to solve a system of linear equations which do not have a full rank in their matrix form. A full rank for a matrix corresponds to a square matrix with a nonzero determinant.
Therefore, the Least Squares method is used to solve the matrices which are not square but rather rectangular. Solving such matrices can be a bit tricky but the Least Squares calculator is here to help with that.

What Is a Least Squares Solution Calculator?
A Least Squares Solution Calculator is a tool that will provide you with your rectangular matrices’ least-squares solutions right here in your browser. You can use this calculator online and solve your Least Squares method problems very easily.
This Calculator is designed to solve specifically 3 x 2 matrix problems as they can’t be solved using the conventional square matrix method. This 3 x 2 order of matrix describes a matrix with 3 rows and 2 columns. You can simply enter place matrix entries into the input boxes of the calculator for use.
How To Use a Least Squares Solution Calculator?
A Least Squares Solution Calculator can be used by first setting up a problem that you would like to solve, and then following the steps provided for its use. It is important to note that this calculator works only for 3 x 2 matrix problems.
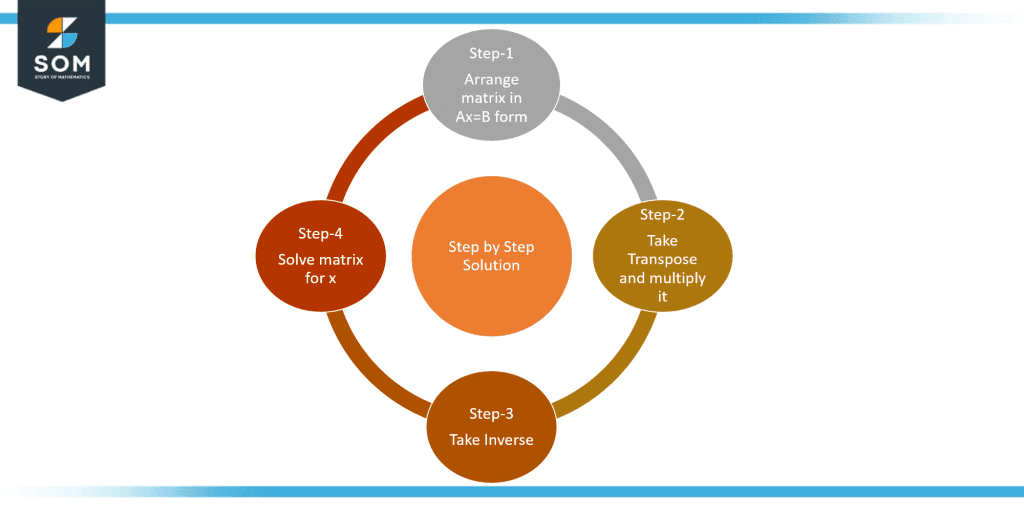
Figure-1 Step By Step Procedure of least Square solution
To find a solution using this calculator, you must have a 3 x 2 A matrix and a 3 x 1 b matrix which is necessary to solve for the resulting 2 x 1 X matrix. Now follow the given steps below to get the best results from this calculator:
Step 1:
You may start by entering the given A matrix’s entries into the input boxes, namely “Row 1 of A”, “Row 2 of A”, and “Row 3 of A”, respectively.
Step 2:
This is followed by a step involving the entry of the b matrix into the input box labeled “b”.
Step 3:
Once you have entered all the inputs, you can simply press the “Submit” button to get the desired solution from the calculator. This step opens the solution to the problem in a new interactable window.
Step 4:
Finally, you can keep solving your problems in the new interactable window if you wish to. You can also close this window by clicking the cross button on the top-right corner at any time.
It is important to note that this calculator won’t be effective against problems with an order of matrix other than 3 x 2. The order 3 x 2 of a matrix is a very common order for problems without a full rank. Therefore, it serves as a great tool for solving such problems.
How Does a Least Squares Solution Calculator Work?
A Least Squares Solution Calculator works by solving a 3 x 2 matrix A’s system of linear equations for a value of vector b. To solve a matrix without a full rank, it is important to note whether the matrix has a rank equal to 2.
The Rank of a Matrix
A matrix A’s rank is defined as its corresponding vector space’s dimension. To solve for rank, one first applies the elementary transformations on the matrix. The transformation should lead to the normal form of the matrix, including an identity matrix I.
The order of the resulting identity matrix I represents the numerical value of the Rank of the given matrix.
Least Squares Method
The least-squares method is used for solving a system of linear equations which don’t have a square matrix associated with them. Another important fact to remember is that you can only apply the Least Squares method on matrices with a Rank higher than 1.
Now, assume there is a 3 x 2 matrix A, and a vector b, which can also be represented as a 3 x 1 matrix. These two can be tied together using a third matrix, namely X of order 2 x 1, which is unknown.
AX = b
To solve this equation for a rectangular matrix, you must convert the matrix A into its least-squares form. This is done by introducing the transpose of A on both sides of the equation.
\[A^{T}AX = A^{T}b\]
Solving the matrix multiplication $A^{T}A$, you get a square matrix of order $2×2$. This matrix is then solved further here:
\[ \hat{X}= (A^{T}A)^{-1}A^{T}b\]
The above equation is the Least Squares solution to the initial system of linear equations given.
Solved Examples
Example No. 1
Consider the matrix A and the vector b given as:
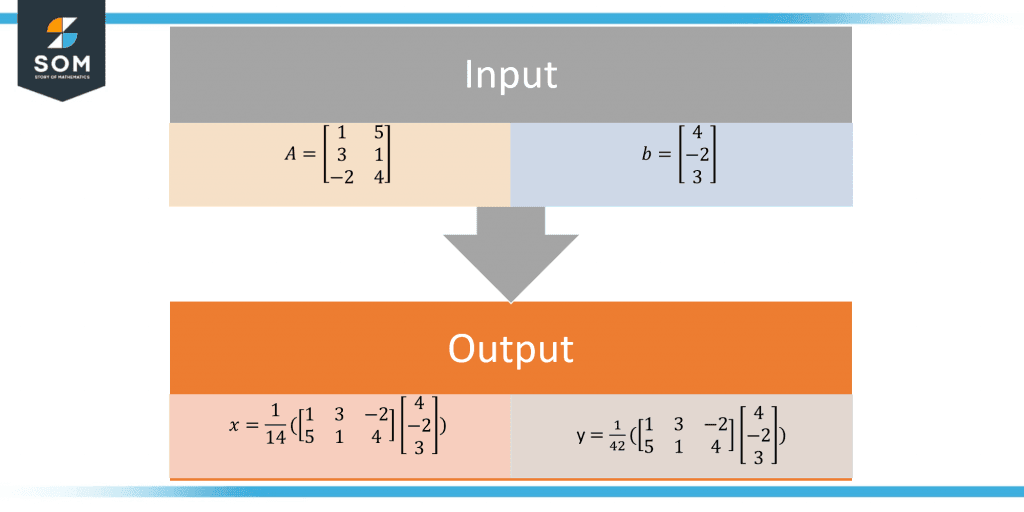
Figure-2 Least Square Solution
\[A=\begin{bmatrix}1&5 \\ 3&1 \\ -2&4\end{bmatrix}, b=\begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\]
Find the matrix X for the above problem.
Solution
We start by arranging the matrices in the form of the equation AX = b.
\[\begin{bmatrix}1&5 \\ 3&1 \\ -2&4\end{bmatrix} X = \begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\]
Now take the transpose of A and multiply it on both sides of the equation:
\[\begin{bmatrix}1&5 \\ 3&1 \\ -2&4\end{bmatrix}^{T} \begin{bmatrix}1&5 \\ 3&1 \\ -2&4\end{bmatrix} X = \begin{bmatrix}1&5 \\ 3&1 \\ -2&4\end{bmatrix}^{T} \begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\]
\[\begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix} \begin{bmatrix}1&5 \\ 3&1 \\ -2&4\end{bmatrix} X = \begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix}\begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\]
Once the matrix multiplications take place, an inverse must be taken, and the values of X can be calculated.
\[\hat{X} = \bigg(\begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix} \begin{bmatrix}1&5 \\ 3&1 \\ -2&4\end{bmatrix}\bigg)^{-1} \begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix}\begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\]
Finally, the solution to this equation leads to the Least Squares answer of the 3 x 2 matrix. It can be expressed as:
\[x = \frac{1}{14} \bigg( \begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix}\begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\bigg), y = \frac{1}{42} \bigg( \begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix}\begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\bigg) \]
Example No. 2
Consider the matrix A and the vector b given as:
\[A=\begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix}, b=\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]
Find the matrix X for the above problem.
Solution
We start by arranging the matrices in the form of the equation AX = b.
\[\begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix} X = \begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]
Now take the transpose of A and multiply it on both sides of the equation:
\[\begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix}^{T} \begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix} X = \begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix}^{T} \begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]
\[\begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix} \begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix} X = \begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]
Once the matrix multiplications take place, an inverse must be taken, and the values of X can be calculated.
\[\hat{X}= \bigg(\begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix} \begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix}\bigg)^{-1} \begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]
Finally, the solution to this equation leads to the Least Squares answer of the 3 x 2 matrix. It can be expressed as:
\[x = \frac{5}{256} \bigg( \begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\bigg), y = \frac{13}{256} \bigg( \begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\bigg) \]
