JUMP TO TOPIC
Reflection Calculator + Online Solver With Free Steps
A Reflection Calculator is used to find a point’s inversion, also referred to as a point reflection. A point reflection is generally described as an isometric transformation of the Euclidean space.
An isometric transformation is a movement that preserves the geometry, whilst Euclidean space is associated with the physical world. This calculator is therefore used to calculate the transformed coordinates for a point about a line.

What Is a Reflection Calculator?
A Reflection Calculator is an online calculator that is used to solve your Euclidean space problems involving point inversions. This calculator will provide you with the solved step-by-step solution for your line transformation associated with a point and its point reflection.
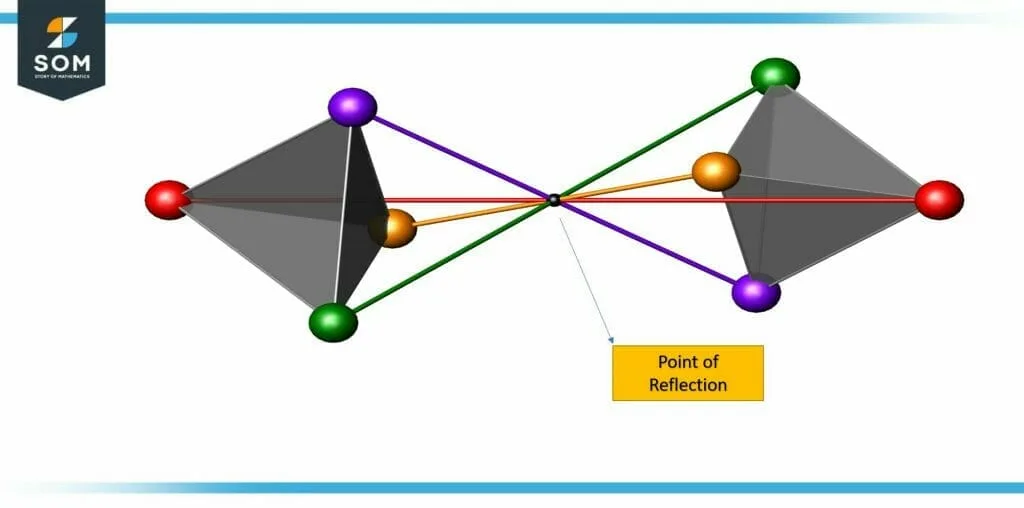
Figure-1 Point of Reflection
The input boxes are available in the calculator, and it is very intuitive to use. The solution can be expressed in several different forms for the user.
How To Use a Reflection Calculator
A Reflection calculator is very straightforward to use, and here is how. You may start by setting up the problem that you want to solve. This problem should have a point for which you intend to calculate the inversion and an equation describing the line on whose side it may lie.
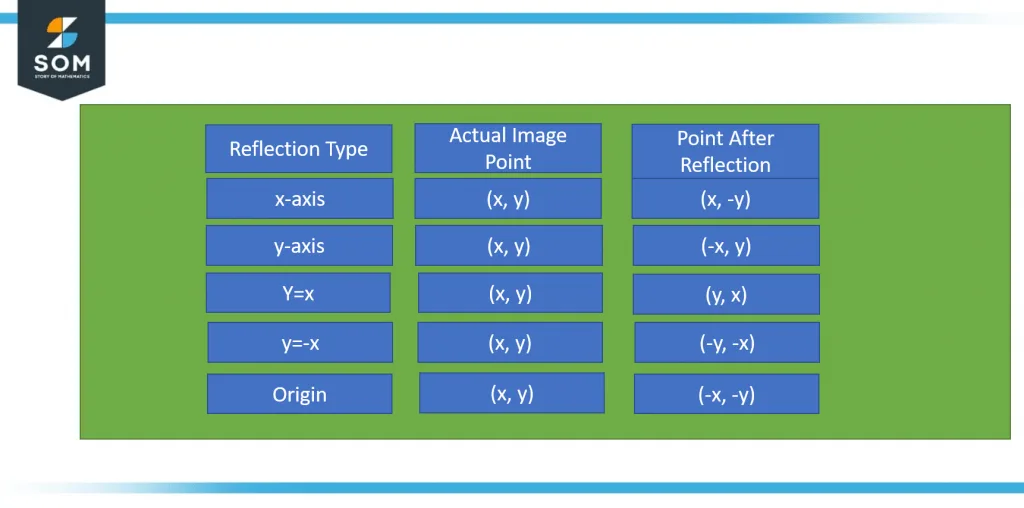
Figure-2 Image Behavior before and after Reflection
Now follow the given steps to achieve the best results for your problems:
Step 1:
You may begin by entering the coordinates of the point of interest.
Step 2:
Follow it up with the entry of the equation of your specified line.
Step 3:
Once the entry is complete, finish up by pressing the “Submit” button. This will open the resulting solution in a new interactable window.
Step 4:
Finally, if you want to solve any more problems of a similar nature, you can do that by entering the new values while in the new window.
It must be noted that this calculator is designed to only work with linear equations and their linear transformations. Any equation above the degree of one will not give a valid solution.
But that doesn’t lower the reliability of this calculator, as it has an in-depth step-by-step solution generator inside it. Therefore, it is a great tool to have up your sleeve.
How Does the Reflection Calculator Work?
The Reflection calculator works by drawing a perpendicular to the line g(x), which is given to us. You draw the line according to the equation and then take the perpendicular to the line so that it includes the point of interest P.
Now, this perpendicular can be elongated over to the point $P^{not}$ on the other side of the line, which we refer to as the point reflection of the original point P. This method can also be called the drawing method. This is used by drawing this graph and measuring the results following the steps given above.
How To Solve Point Reflection Using the Mathematical Approach
The solution to a point reflection problem for a given point and a line segment is very straightforward, and this is how it’s done. You may assume a point P = (x, y), which is the point whose reflection you want to find.
Now, you may also assume a line given by the function, g(x) = m. x + t, on either side of which your original point lies. Finally, you may consider the point reflection that exists for the line g(x), referred to as $P^{not}$. With all these given quantities, one can easily solve for point inversion using the following steps:
- We start off by first calculating the equation of perpendicular s(x) for the given line g(x). This perpendicular is given as: s(x) = ms .x + t. One thing to note is that ms = – 1/m, hinting that P may lie on a line s that coincides with the line g.
- After rearranging the equation, you may get t = y – ms . x as the resulting expression.
- Comparing this final expression with the definition of g(x) would now give us the value of x, considering that g and s would have a point in common.
- Finally, solving the equation g(x) = s(x) would lead to a viable result for the values of x and y. Once you have those values, you can eventually find out the coordinates of $P^{not}$.
Solved Examples
Example 1
Consider the point of interest P(3, -4), and find its reflection around the line y = 2x – 1.
Figure 3 Basic steps to solve reflection point problems
Solution
We start with the description of the mirror line, which would be described as y = -1 + 2x.
Now solving for the transformation of the point $P$, we get:
\[Transformed Points : (3, -4) \rightarrow \bigg ( \frac{-21}{5} , \frac{-2}{5}\bigg )\]
Then the system describes a reflection matrix, which is given as:
\[Reflection Matrix : \begin{bmatrix} -\frac{3}{5} & \frac{4}{5} \\ \frac{4}{5} & \frac{3}{5} \end{bmatrix} \]
Following the reflection matrix is the transformation itself:
\[Transformation : (x, y) \rightarrow \bigg ( \frac{1}{5}(-3x + 4y + 4) , \frac{1}{5}(4x + 3y – 2)\bigg )\]
Finally, the transformation is expressed in its matrix form, and it is as follows:
\[Matrix Form : \begin{bmatrix} x \\ y \end{bmatrix} \rightarrow \begin{bmatrix} \frac{4}{5} \\ -\frac{2}{5} \end{bmatrix} + \begin{bmatrix} -\frac{3}{5} & \frac{4}{5} \\ \frac{4}{5} & \frac{3}{5} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]
Example 2
Consider the point of interest P(4, 2), and find its reflection around the line y = 6x – 9.
Solution
We start with the description of the mirror line, which would be defined as y = 9 + 6x.
Now solving for the transformation of the point P, we get:
\[Transformed Points : (4, 2) \rightarrow \bigg ( \frac{-224}{37} , \frac{136}{37}\bigg )\]
Then, the system describes a reflection matrix, which is given as:
\[Reflection Matrix : \begin{bmatrix} -\frac{35}{37} & \frac{12}{37} \\ \frac{12}{37} & \frac{35}{37} \end{bmatrix} \]
Following the reflection matrix is the transformation itself:
\[Transformation : (x, y) \rightarrow \bigg ( \frac{1}{37}(12(y – 9) – 35x) , \frac{1}{37}(12x + 35y + 18)\bigg )\]
Finally, the transformation is expressed in its matrix form, and it is as follows:
\[Matrix Form : \begin{bmatrix} x \\ y \end{bmatrix} \rightarrow \begin{bmatrix} -\frac{108}{37} \\ \frac{18}{37} \end{bmatrix} + \begin{bmatrix} -\frac{35}{37} & \frac{12}{37} \\ \frac{12}{37} & \frac{35}{37} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]
