JUMP TO TOPIC
Point Slope Form Calculator + Online Solver With Free Steps
The online Point Slope Form Calculator is a calculator that allows you to represent a straight line in a linear equation form.
The Point Slope Form Calculator is a powerful tool that helps mathematicians and scientists to find the point-slope form of a line.

What Is a Point Slope Form Calculator?
A Point Slope Form Calculator is an online tool that helps you determine the point-slope form of a calculator of a straight line.
The Point Slope Form Calculator requires two inputs: the value of the slope and the points the line passes. Using the inputs, the Point Slope Form Calculator quickly calculates the point slope from the line.
How To Use a Point Slope Form Calculator?
To use the Point Slope Form Calculator, you will need to input the data of the line in their respective boxes and click the “Submit” button. The calculator will display the results in a new window.
The detailed instructions for using a Point Slope Form Calculator are given below:
Step 1
First, we add the value of the slope into the Point Slope Form Calculator.
Step 2
After adding the value of the slope, we add the points where the line passes through in the Point Slope Calculator.
Step 3
Once we have entered both these inputs, we click the “Submit” button present on the Point Slope Form Calculator. The calculator displays the point-slope form and a graph in a separate window.
How Does a Point Slope Form Calculator Work?
The Point Slope Form Calculator works by taking in the inputs and turning the line equation into the point-slope form. The point-slope form is generally represented as the following equation:
y – y1 = m ( x – x1 )
What Are Linear Equations?
A linear equation is an equation in which the variable’s maximum power is consistently 1; another name for this is a one-degree equation. A linear equation with one variable has the following standard form:
Ax + B = C
A is a coefficient, B is constant, and x is a variable in this situation. A linear equation is also known as a linear equation because it always produces a straight line when all possible solutions are graphed.
It makes no difference if you use whole integers, fractions, decimals, etc., for the x and y values. Each answer pair is on the graphed line. Nearly every part of life can benefit from using linear equations.
Examples include computing distance, calculating hourly pay, figuring out how much to charge in banking and engineering, and calculating how much medication to administer to a patient based on their weight and age.
A linear equation for a graph is usually represented by:
y = mx + c
Point Slope Form
The point-slope form calculates the equation of a straight line inclined to the x-axis at a certain angle and passes through a particular point. The equation of a line is an equation that is satisfied by every point on the line. This indicates that a linear equation with two variables represents a line.
Multiple methods are used to find the equation of a line depending on the information given. When we know the slope of a line and a point on it, we may utilize the point-slope formula.
The point-slope form expresses a straight line by using its slope and a point on the line. The equation of a line with slope m and passing through a point (x1, y1) is determined using the point-slope form.
Formula for Point Slope Form
The point-slope form formula is used to calculate the equation of a line. The point-slope form is used to calculate the equation of a line with a specified slope and a given point.
This formula is only utilized when the slope of the line and a point on the line are known. Other formulas for determining the equation of a line include slope-intercept form, intercept form, and so on. The point-slope formula is as follows:
y – y1 = m ( x – x1 )
Where:
Random point on line = (x,y)
Fixed point on the line = (x1, y1)
m = Slope of the line
Deriving the Point Slope Form Formula
The point-slope formula is derived using the equation for the slope of the line. Consider a line with slope m. Assume that (x1, y1) is a known point on the line. Let (x, y) be any other random point on the line with unknown coordinates.
We know that the equation for a line’s slope is:
\[ m = \frac{(y-y_{1})}{(x-x_{1})}\]
We multiply (x- x1) on both sides and get:
m(x – x1) = (y – y1)
Which can be written as:
y – y1 = m ( x – x1 )
Hence this derivation proves the formula.
Solved Examples
The Point Slope Form Calculator instantly allows you to find the point-slope form of a linear graph.
The following are some examples solved using the Point Slope Form Calculator:
Solution
Using the Point Slope Form Calculator, we can easily find the point-slope form of the graph. Initially, we enter the value of the slope into the Point Slope Form Calculator; the value of the slope is 4. After entering the slope value, we enter the point where the line passes through in our calculator; the point where the line passes through is (2,5).
After entering the slope’s value and the point where the line passes through in their respective boxes, we click the “Submit” button on the Point Slope Form Calculator. The calculator immediately displays the results and plots the graph in a separate window.
The following results are extracted from the Point Slope Form Calculator:
Input Interpretation:
Line:
Slope = 4
Through = (2,5) Cartesian Plane
Result:
y = 4x – 3
Visual Representation:
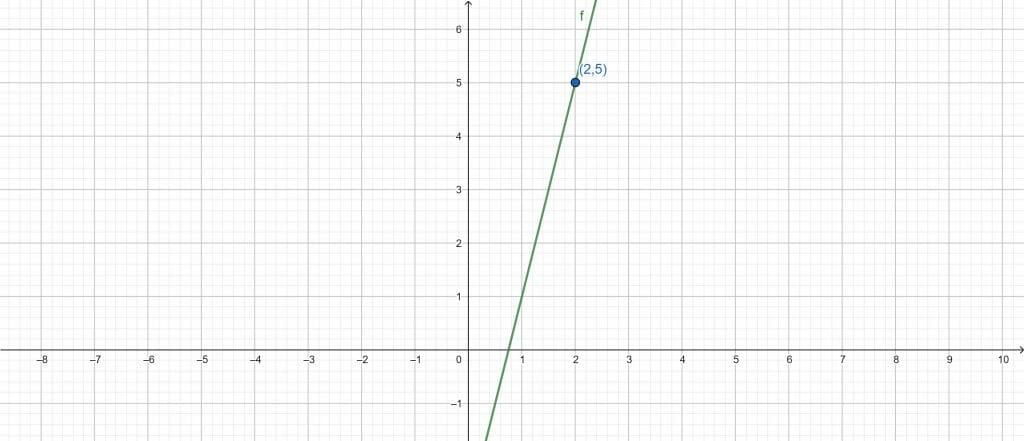
Figure 1
Properties of line:
x intercept : $\frac{3}{4}$ = 0.75
y intercept : -3
Example 2
During an assignment, a college student came across a linear graph with a slope value of 3, and the line passed through the point (-1,2). To complete his assignment, the student had to find the point-slope form of the linear graph. With the help of the Point Slope Form Calculator, find the point-slope form of the linear graph.
Solution
Using the Point Slope Form Calculator, we can quickly determine the graph’s point-slope form. First, we enter the slope value into the Point Slope Form Calculator; the slope value is 3. We input the point where the line passes through our calculator after entering the slope value; the point where the line goes through is (-1,2).
We press the “Submit” button on the Point Slope Form Calculator after entering the slope’s value and the point where the line passes through their corresponding boxes. The calculator displays the findings immediately and plots the graph in a separate window.
The Point Slope Form Calculator produced the following results:
Input Interpretation:
Line:
Slope = 3
Through = (-1,2) Cartesian Plane
Results:
y = 3x + 5
Visual Representation:
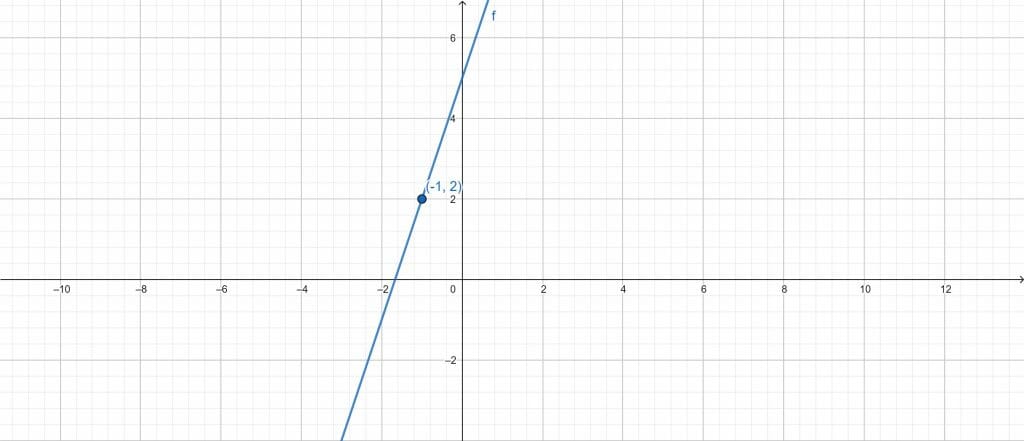
Figure 2
Properties of line:
x intercept : – $\frac{5}{3}$ $\approx$ 1.66667
y intercept : 5
Example 3
A mathematician needs to find the point-slope form of a linear graph. The linear graph has a slope value of -5 and passes through the point (4,-3). Using the information provided, find the point-slope form of the linear graph.
Solution
We can quickly determine the point-slope form of the graph using the Point Slope Form Calculator. First, we enter the slope’s value into the Point Slope Form Calculator; the value of the slope is -5. After entering the slope value, we enter the point where the line goes through into the Point Slope Calculator. The point where the line goes through is (4,-3).
The slope value and the point where the line intersects are entered into the corresponding fields on the Point Slope Form Calculator before clicking the “Submit” button. The Point Slope Form Calculator shows the results immediately, and a separate window is used to plot the graph.
The following results are generated using the Point Slope Form Calculator:
Input Interpretation:
Line:
Slope = -5
Through = (4,-3) Cartesian Plane
Results:
y = 17 – 5x
Visual Representation:
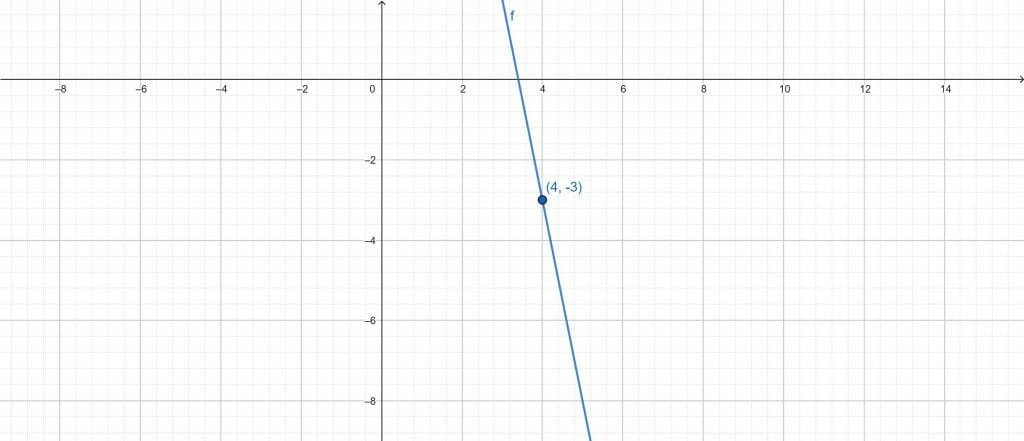
Figure 3
Properties of line:
x intercept : – $\frac{17}{5}$ = 3.4
y intercept : 17
Example 4
Consider the following values of a linear graph:
Slope = 2
Line passing through = (1,2)
Use the information above to find the point-slope form of the linear graph.
Solution
We can easily find the point-slope form using the Point Slope Form Calculator. We add the information we are provided into their respective boxes in the Point Slope Form Calculator. Click the “Submit” button, and the calculator will generate the results.
The following results are generated from the Point Slope Form Calculator:
Input Interpretation:
Line:
Slope = 2
Through = (1,2) Cartesian Plane
Results:
y = 2x
Visual Representation:
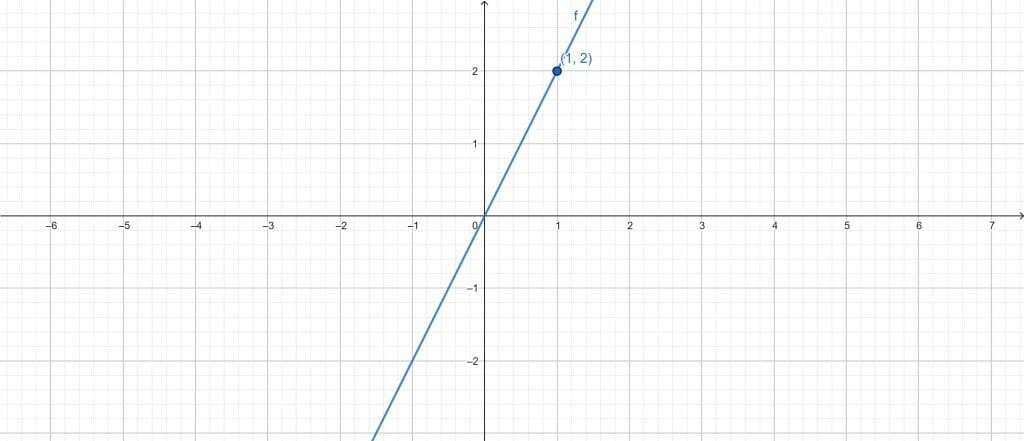
Figure 4
Properties of line:
x intercept : 0
y intercept : 0
All images/graphs are made using GeoGebra.
