JUMP TO TOPIC
Product Calculator + Online Solver With Free Steps
The online Product Calculator helps you find the product of any given series of numbers. The value and number are provided as input to the calculator.
Product means the multiplication of a number with numbers up to a specific value. This product is represented by the symbol of the pie (𝝥).
The calculator shows the final value after series multiplication. It also outputs graphs that show the partial product of numbers.

What Is the Product Calculator?
The Product Calculator is an online calculator that calculates the finite multiplication from one specific value to a certain given value with an increment of 1 from starting value to the end value in each step.
To calculate the product for a series of values we need to input two values into the calculator. The first one will be the starting value and the second will be the end value.
The calculator will multiply all the numbers from the first value to the second value with an increment of 1 unless it reaches the second value.
The concept of the Product is widely used in solving mathematics problems, calculations, and life problems like pricing the products.
Simple product Calculations can be made easily but if we have a huge set of data, it becomes very complex and difficult to handle. But with this online free Product Calculator, we can perform complex calculations in a few seconds easily.
Also, to display the multiplication of a series of products we need to plot the graph which is again a tedious task. But this Product Calculator also performs this task quickly.
There is no prior requirement of installing apps or other formalities, you can just use your browser to use this calculator.
How To Use the Product Calculator?
You can use the Product Calculator by putting two different values in the given boxes. You need to follow the user-friendly steps below to use the Product Calculator correctly.
Step 1
Enter the variable name in the box with the name ‘Product of’ and enter the same variable in the second box with the name ‘from’. Otherwise, you can leave the boxes in default condition with the variable name ‘k’.
Step 2
Now, enter your initial value in the next box which is represented by =. In the last box with the name ‘to’ enter the value up to which you want to find the product.
Step 3
Now simply click the Submit button to get the calculator’s answer.
Result
The result consists of two sections. The first section shows the direct answer of the product with the symbolic representation of the product in the pie symbol.
The next section shows the Partial Graph of the product. The X-axis represents the values being multiplied while the Y-axis represents the result of the product. This plot for the product can help you better understand the process of series multiplication.
How Does the Product Calculator Work?
The product calculator works by finding the product of a series of values between the given range and plotting it on the cartesian coordinate system. This calculator can find the product of any type of value including exponential, trigonometric, and absolute values.
Before going into the detailed workings of the Product calculator, we should know about multiplication.
What Is Multiplication?
Multiplication is the short method of addition. It is the addition of the same numbers many times. For example:
3 x 6 = 18
It is the same as:
3+3+3+3+3+3 =12
Or:
6+6+6 =18
Series Multiplication
Series Multiplication is the multiplication of several numbers between two know values with the increment of 1.
This Product Calculator performs the series multiplication. This calculator performs the multiplication with the Pi symbol, Ⲡ. The product is a repeated multiplication with a start value and an end value.
Running Variable
A running variable is also used which is increased by 1 in each step. Only this variable occurs in terms of the product. All the basic arithmetic operations can be performed.
Process
The calculator first multiplies the start number with an increment of one in itself, then the result of the first multiplication is multiplied with another increment of 1 in the start value and this process continues till the end value reaches.
Result
The result is the product of all the terms of the series from the start value to the end. The answer can be a whole number or a decimal number depending on the input values.
Pi ( 𝝥 ) Symbol Representation
The upper case pi symbol tells that the expression begins at a value, which is written below the product, and evaluates it till a value is written on the top.
Graph
The graph is plotted for the series multiplication which shows the trend of multiplication throughout the process.
Solved Examples
Now let’s solve some examples by using Product Calculator. Each example is described below.
Example 1
Find the product of k from k equals 2 to 10.
Solution
It finds the values of the expression at each value of k as follows
2 x 3=6
6 x 4=24
24 x 5=120
120 x 6=720
720 x 7=5040
5040 x 8=40320
40320 x 9=362880
362880 x 10=3628800
Result
So, the product of k from k=2 to 10 is 3628800
\[\prod_{k=2}^{10}k=3628800\]
Graph
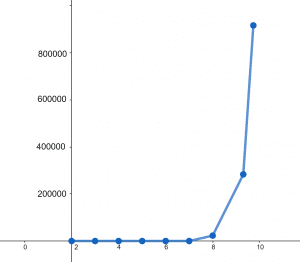
Figure 1
Example 2
Find the product of k from k equals 3 to 9.
Solution
The Product calculator finds the values of the expression at each value of k as follows
3 x 4=12
12 x 5=60
60 x 6=360
360 x 7=2520
2520 x 8=20160
20160 x 9=181440
Result
So, the product of k from k=3 to 9 is 181440
\[\prod_{k=3}^{9}k=181440\]
Graph
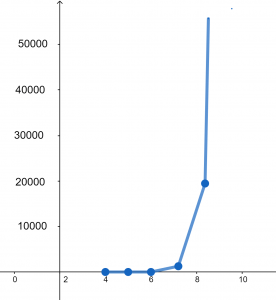
Figure 2
Example 3
Find the product of k from k equals 1 to 4.
Solution
The Product calculator finds the values of the expression at each value of k as follows
1 x 2=2
2 x 3=6
6 x 4=24
Result
So, the product of k from k=1 to 4 is 24
\[\prod_{k=1}^{4}k=3628800\]
Graph
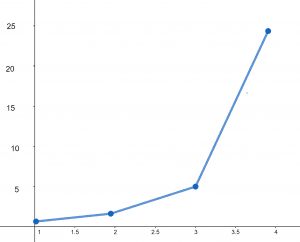
Figure 3
All the mathematical images/graphs are created using GeoGebra.
