Polar Form Calculator + Online Solver With Free Easy Steps

The online Polar Form Calculator helps you easily convert a complex number into its polar form.

The Polar Form Calculator proves to be a powerful tool for mathematicians, allowing them to convert a complex number into its polar form instantly. This time-consuming conversion is done in an instant using the Polar Form Calculator.

What Is a Polar Form Calculator?

The Polar Form Calculator is an online calculator that takes complex numbers and expresses them in their polar form.

The Polar Form Calculator only needs a single input. This input is a complex number. After you plug in your complex number, you must click the “Submit” button. The Polar Form Calculator will display the polar form of the complex number you provided. 

The Polar Form Calculator displays several results, such as the type of conversion, polar coordinates, cartesian coordinates, and a graph representing the position of a complex number in the complex plane.

How To Use a Polar Form Calculator?

You can use a Polar Form Calculator by just entering the complex number and clicking the Submit button. You are instantaneously presented with the results in a separate window. 

The step-by-step instructions on how to use a Polar Form Calculator are given below:

Step 1

First, you plug your complex number into the Polar Form Calculator box.

Step 2

After entering your complex number, click on the “Submit” button. Once you click the button, the Polar Form Calculator gives you the results in a new window.

How Does a Polar Form Calculator Work?

The Polar Form Calculator works by converting a given complex number into a polar form through calculations. The complex number z = a +ib is changed to its polar form by applying the Pythagoras theorem and trigonometric ratios to the complex number.

To further understand the working of a calculator, let’s explore some important concepts involved.

What Are Complex Numbers?

Complex numbers are the numbers that are the combination of a real number and an imaginary number. Complex numbers serve as the foundation for more complex math, including algebra. They have various practical applications, particularly in electronics and electromagnetism.

A complex number is typically symbolized by the symbol z and has the form a + ib, where a and b are real numbers, and i is the imaginary number. The i is called the iota, which has a value of $ \sqrt{-1} $. Technically, any real number or imaginary number can be regarded as a complex number. Hence, either portion could be 0.

Complex does not imply complicated; rather, it indicates that the two types of numbers combine to create a complex, similar to a housing complex, which is a collection of connected structures.

Real numbers, including fractions, integers, and any other countable number you can conceive, are quantifiable quantities that may be plotted on a horizontal number line. In contrast, imaginary numbers are abstract values used when you need the square root or use a negative number.

Complex numbers allow us to solve any polynomial equation. For example the equation $x^{2} – 2x + 5 = 0 $ does not have any real or imaginary solutions. However, it does have a complex solution which are 1 + 2i and 1 – 2i.

How Is a Complex Number Graphed?

A complex number is graphed using both its real and imaginary numbers, which can be thought of as an ordered pair (Re(z), lm(z)) and can be visualized as coordinate pairs on a Euclidean plane.

The complex plane, often known as the Argand Plane after Jean-Robert Argand, is the term given to the Euclidean plane with respect to complex numbers. The real part, $a$, and the imaginary part, ib, are used to depict the complex number z = a + ib about the x-axis and the y-axis, respectively.

What Is a Modulus of a Complex Number?

The modulus of a complex number is the distance between a complex number and a point on the argand plane (a, ib). This distance, which is measured as $r = \sqrt{| a^{2} + b |}$, is a linear one from the origin (0, 0) to the point (a, ib).

Additionally, this can be seen as deriving from the Pythagoras theorem, where the modulus represents the hypotenuse, the real component represents the base, and the imaginary portion represents the altitude of the right-angled triangle.

What Is an Argument of a Complex Number?

The argument of a complex number is the anticlockwise angle formed by the positive x-axis and the line connecting the complex number’s geometric representation and the origin. The complex number’s argument is the inverse of the tan result of the imaginary part divided by the real part, as shown below:

\[ Arg z(\theta ) = \tan^{-1}(\frac{b}{a}) \]

What Is a Polar Form of a Complex Number?

The polar form of a complex number is another form of representing complex numbers. The rectangular form of a complex number is represented by the formula z = a+bi, where (a, b) are its rectangular coordinates. The modulus and argument of the complex number are used to indicate the polar form. The polar form coordinates were invented by Sir Isaac Newton.

Complex numbers are expressed as the complex number’s modulus r and argument $\theta$ when they are in polar form. Complex number z = x + iy with coordinates (x, y) has the following polar form:

z=r cos{$\theta$}+ir sin{$\theta$}= r (cos{$\theta$} + i sin{$\theta$}) 

How Are Polar Forms Used in Real-Life?

Polar forms of numbers are used in several scientific applications such as physics, mathematics, and electronics. Polar coordinates (r and $\theta$ ) are helpful from a physicist’s perspective in computing the equations of motion from numerous mechanical systems.

A technique known as the Lagrangian and the Hamiltonian of a system can be used to analyze the dynamics of objects that frequently move in circles. For this technique, polar coordinates are a far better way to simplify things than cartesian coordinates.

Polar coordinates can be used in 3D(spherical coordinates) systems and mechanical systems. This will much aid calculations on fields. Examples include magnetic, electric, and thermal areas.

Polar coordinates simplify calculations for physicists and engineers, to put it briefly. We now have more advanced machinery and a better knowledge of the principles of electricity and magnetism, which are crucial for producing power.

Solved Examples

The Polar Form Calculator can easily convert a complex number into its polar form. Here are some examples that were solved using the Polar Form Calculator.

Example 1

A college student is given a complex number: 

7 – 5i 

The student needs to find the polar form of the complex number. Find the polar form of the complex number given above.

Solution

We can quickly solve this example by using the Polar Form Calculator. First, we enter the complex number 7 – 5i into its respective box. 

After entering the equation, we click the “Submit” button. A new window is opened, displaying the polar coordinates of the complex number, the cartesian points, and a graphical representation of the complex numbers.

The Polar Form Calculator shows the following results:

Input interpretation:

Convert 7 – 5i from rectangular form to polar form 

Polar Trigonometric:

\[ \sqrt{74} (\cos(\tan^{-1}(\frac{5}{7}))+i\sin(\tan^{-1}(\frac{5}{7}))) \]

Polar Exponential:

\[ \sqrt{74}\ e^{\tan^{-1}(\frac{5}{7})i} \]

Polar Coordinates:

\[ (r,\theta)=(\sqrt{74},\tan^{-1}(\frac{5}{7})) \]

Cartesian Coordinates:

(x,y) = (7,-5) 

Position in the complex plane:

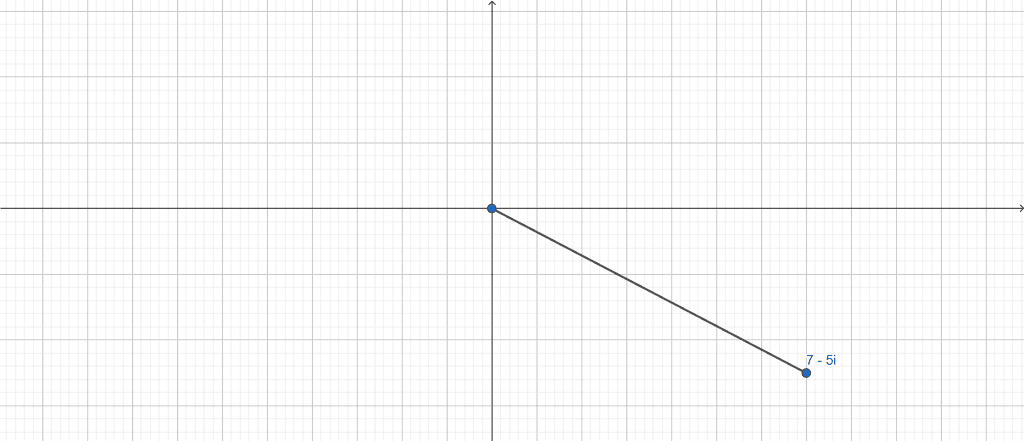
Figure 1

Example 2

While researching electromagnets, a scientist derived the following complex number:

3 –  2i 

To further complete his research, the scientist needs to convert the complex number into a polar form. Find the polar form of the given complex number.

Solution

By using the help of our Polar Form Calculator, we can instantly convert the complex number into its polar form. First, we plug our complex number 3-2i into our Polar Form Calculator.

After entering our equation into the calculator, we click the “Submit” button. The Polar Form Calculator performs the necessary calculations and displays all the results.

The Polar Form Calculator gives us the following results:

Input interpretation:

Convert 3 – 2i from rectangular form to polar form 

Polar Trigonometric:

\[ \sqrt{13} (\cos(\tan^{-1}(\frac{2}{3}))+i\sin(\tan^{-1}(\frac{2}{3}))) \]

Polar Exponential:

\[ \sqrt{13}\ e^{\tan^{-1}(\frac{2}{3})i} \]

Polar Coordinates:

\[ (r,\theta)=(\sqrt{13},\tan^{-1}(\frac{2}{3})) \]

Cartesian Coordinates:

(x,y) = (3,-2) 

Position in the complex plane:

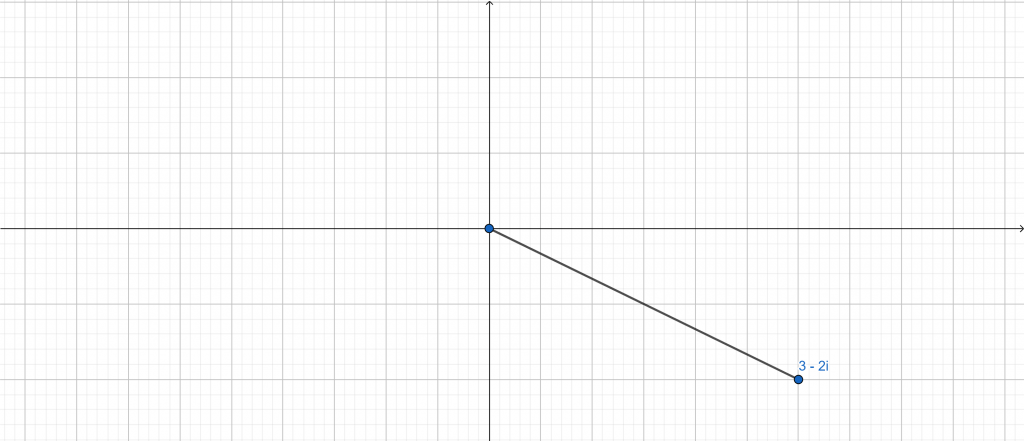
Figure 2

Solved Example 3

While completing his assignment, a student comes across the following complex number:

10 + 8i 

To complete his assignment, the student must find the complex number’s polar form and plot it in a graph. Find the polar form and plot a graph.

Solution

To solve this particular example, we will use our Polar Form Calculator. Initially, we input our complex number 10 + 8i in the Polar Form Calculator. Once the complex number is added to our calculator, we can easily find the results by clicking the “Submit” button.

The Polar Form Calculator opens a new window and gives us the following results:

Input interpretation:

Convert 10 + 8i from rectangular form to polar form 

Polar Trigonometric:

\[ \sqrt[2]{41} (\cos(\tan^{-1}(\frac{4}{5}))+i\sin(\tan^{-1}(\frac{4}{5}))) \]

Polar Exponential:

\[ \sqrt[2]{41}\ e^{\tan^{-1}(\frac{4}{5})i} \]

Polar Coordinates:

\[ (r,\theta)=(\sqrt[2]{41},\tan^{-1}(\frac{4}{5})) \]

Cartesian Coordinates:

 (x,y) = (10,8) 

Position in the complex plane:

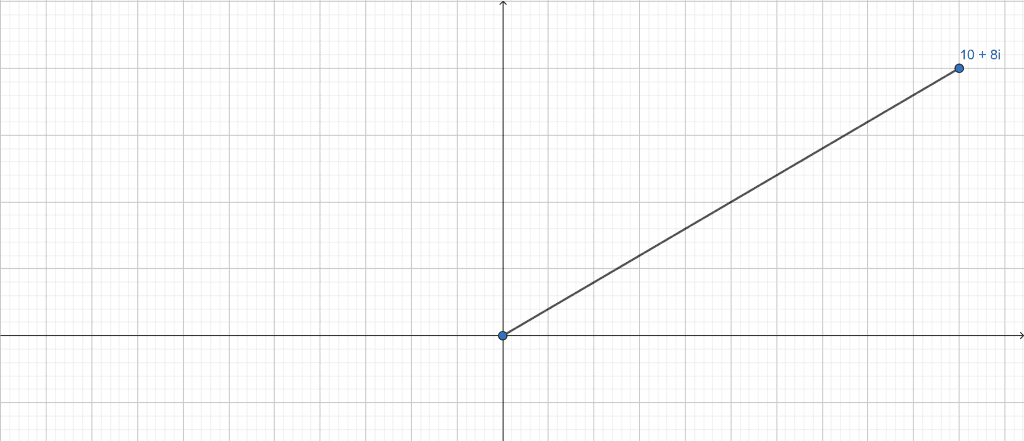
Figure 3

All Mathematical images/graphs are created using GeoGebra.

Lewis Structure Calculator < Math Calculators List > Solids Of Revolution Calculator