JUMP TO TOPIC
Solids of Revolution Calculator + Online Solver With Free Steps
The Solids of Revolution Calculator is an online calculator that is used to calculate the volume of solids that revolved around any particular axis, either horizontal or vertical.
This calculator provides quick and accurate results for calculating the volumes of such solids. The Solids of Revolution Calculator is a free tool that uses the formula incorporating the definite integral to calculate the volume of solids of revolutions.
This calculator takes the function, the boundaries, and the axis around which the solid is revolved from the user as input.
What Is the Solids of Revolution Calculator?
The Solids of Revolution Calculator is an extremely handy online calculator that is used to calculate the volume of solids that undergo revolution around a specific axis, be it x, y, or z.
This calculator uses the definite integral to calculate the volume of such solids.
The Solids of Revolution Calculator provides the results in both mathematical as well as graphical forms. This calculator simply takes the function and the boundaries from the user as input, along with the axis around which the solid is revolved.
The best feature of the Solids of Revolution Calculator is that it presents the answer in three-dimensional graphical form so that the user can visually interpret the desired results. Moreover, this calculator provides accurate and quick results which further enhances its efficiency.
The Solids of Revolution Calculator makes use of the following formula for calculating the volume of solids undergoing revolution:
\[ V = \pi \int_{a}^{b} f(x)^{2} dx \]
In this formula, the $a$ and $b$ limits correspond to the axis around which the solid undergoes a revolution. The function f(x) in this formula, corresponds to the curve of the solid.
Moreover, the integral also corresponds to the axis around which the solid is rotated. In this case, the solid undergoes revolution around the x axis.
For instance, if a solid undergoes revolution around the y axis, then the following formula is used:
\[ V = \pi \int_{a}^{b} g(x)^{2} dy \]
Usage of this formula gives the volume of the solid under the action of revolution.
How To Use the Solids of Revolution Calculator?
You can use the Solid of Revolution calculator by directly entering the function and specifying the axis about which the curve occurs. It is fairly easy and simple to use due to its user-friendly interface. Its interface is quite simple and the user can easily navigate through it to get the desired output.
The Solids of Revolution Calculator is not only easy to use, but also provides quick results within a matter of a few seconds. This calculator consists of 4 input boxes and a button that says “Submit.”
The four input boxes of this calculator are used to take different inputs from the user. The first input box is titled “Curves” and it is used to enter the function of the solid. This function corresponds to the curve of the solid.
The next input box has the title “Axis” and it prompts the user to enter the axis around which the revolution takes place.
The third and fourth input boxes are labeled with “To” and “From” respectively and they prompt the user to enter the starting initial boundary and the final boundary of the function of the solid.
For a much more comprehensive understanding, given below is a step-by-step guide for using the Solids of Revolution Calculator.
Step 1
Analyze the function, which is the curve of the solid, and the axis around which you need to revolve your solid.
Step 2
Enter the first input into the calculator. This first input is the function of the solid. This function is also known as the curve of the solid and it goes into the box entitled “Curves.”
Step 3
Next up, insert the axis around which you need to revolve your solid.
Step 4
Moving on, enter the boundaries of the revolution of the solid. Enter the starting boundary point a into the “From” input box and the ending boundary point b into the “To” input box.
Step 5
Once all the input values have been inserted, click the “Submit” button. The calculator will take a few seconds to load the solution and then it will present the solution in both mathematical and graphical terms.
How Does the Solids of Revolution Calculator Work?
The Solids of Revolution Calculator works by using the most fundamental principle of calculus, the definite integral. to determine the volumes of various solids once they are revolved around a particular axis.
To enhance your concept of using the Solids of Revolution Calculator, let’s review the concept of solids of revolution.
What Is Solids of Revolution?
The Solids of Revolution is a 3-D figure obtained by revolving the curve along any axis of revolution. It is one of the most crucial concepts in calculus and also in geometry. It deals with volumes of solids existing in a three-dimensional space.
The solids are obtained by revolving their curves or lines around a particular axis, either horizontal or vertical. The revolution of these functions generates a three-dimensional solid whose volume can then be calculated,
The concept of solids of revolution can be extended to the Washer method as well as the Shell method.
Solved Examples
Given below is a solved example that can help you develop a better understanding of using the Solids of Revolution Calculator.
Example 1
Find the volume of the following function, given that the function is revolved around the $y$ axis from 0 to 1. The function is given below:
\[ y = x^{2} \]
Solution
Before using the calculator, the first step is to analyze the function and the axis around which the function is revolved.
The function is given below:
\[ y = x^{2} \]
It is also stated that the function is revolved around the y axis, which is the vertical axis.
Moreover, the boundary of the function is also given which is from 0 to 1.
Next up, simply insert all the values in the designated input boxes.
Once all the values have been inserted, simply click on the Submit button. The calculator will take a few seconds to load and then it will make use of the following formula for the volume calculation:
\[ V = \pi \int_{a}^{b} f(x)^{2} dx \]
The following solid revolution plot is obtained because of the revolution of the curve around the y-axis as shown in figure 1:
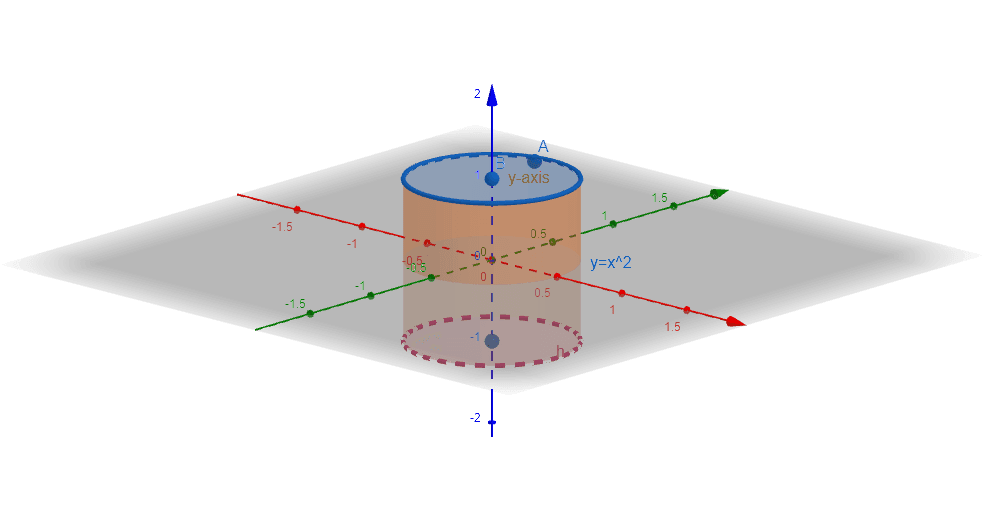
Figure 1
All the Mathematical Images/Graphs are created using GeoGebra.
