JUMP TO TOPIC
Profit Function Calculator + Online Solver With Free Steps
The Profit Function Calculator determines the profit function P(q) and its derivative P’(q) from the given revenue and cost functions R(q) and C(q). The variable q can be considered the quantity of the product.
The calculator does not support multi-variable functions for any of the three quantities. If some other variable replaces q (such as x or y), the calculator performs differentiation with respect to that variable. Some characters such as ‘a,’ ‘b,’ and ‘c’ are considered constants and do not affect the calculations.
The cost function models the various costs associated with the product’s creation and marketing, while the revenue function goes through all the channels that generate income through sales (revenue). Depending on the models used, the functions themselves, and various complex real-world scenarios, the cost function may be linear or non-linear.
You can use the profit function to find the break-even condition by setting P(q)=0 for zero profit. Furthermore, you can find the maximum profit condition by finding the derivative P’(q), setting it equal to zero, and solving for q. The second derivative test can then be applied to ensure this is the maximum profit condition.

What Is the Profit Function Calculator?
The Profit Function Calculator is an online tool that finds an expression for the profit function P(q) as well as its derivative P’(q) given the revenue R(q) and cost C(q) functions.
The calculator interface consists of two text boxes labeled “R(q)” and “C(q).” They take the expression for revenue and cost function respectively as input, after which the calculator computes the profit function.
The profit function represents the difference between the revenue and cost function:
P(q) = R(q)-C(q)
The calculator further differentiates the above equation with respect to q:
\[ P’(q) = \frac{d}{dq} \left( R(q)-C(q) \right) \]
That can be used to find the maximum profit condition if it exists. Thus, the calculator helps solve optimization problems.
How To Use the Profit Function Calculator?
You can use the Profit Function Calculator by entering the revenue and cost functions into the two text boxes and pressing the submit button to have the calculator evaluate the expression for the profit function.
For example, let us assume we have:
R(q) = -$5q^2$ + 37q
C(q) = 10q + 400
And we want to find the profit function and its derivative for optimization at a later stage. The step-by-step guidelines to do so using the calculator are below:
Step 1
Enter the revenue function into the first text box labeled “R(q).” For our example, we enter “-5q^2+37q” without quotes.
Step 2
Enter the cost function into the second text box labeled “C(q).” We enter “10q+400” without quotes in our case.
Step 3
Press the Submit button to get the resulting profit function P(q) and its derivative P’(q).
Results
For our example, the result turns out to be:
\[ P’(q) = \frac{d}{dq} \left\{ -5q^2 + 37q-\left( 10q + 400 \right) \right\} \]
P’(q) = 27-10q
Where $R(q) = 5q^2 + 37q-\left( 10q + 400 \right) = -5q^2 + 27q + 400$ is the revenue function. The results also display the input interpretation, which you can use to verify that the calculator handles the input as intended.
Solved Examples
Example 1
As a fedora lover, Mr. Reddington hopes to revive the once mighty age of the dapper hats in the contemporary world. To sustain the business, he has to maximize the profit on the initial sales. The per-unit cost to produce a fedora with the people he currently works with is 15 USD. Additionally, a fixed cost of 200 USD on other expenditures is expected.
The price-demand function in dollars per hat has been set as p(q) = 55-1.5q. Mr. Reddington wants you to find the number of hats q to manufacture that would maximize his profit. In case of any hiccups in the supply chain, he also wants you to find the break-even cost.
Solution
Note that we do not have the revenue and cost function right now. Using the information from the example statement, we find the cost function:
C(q) = 15q + 200
And from the price-demand function p(q), we can get the revenue function by simply multiplying the number of hats q:
R(q) = q . p(q) $\Rightarrow$ R(q) = q(55-1.5q)
R(q) = 55q-1.5$q^2$ = -$1.5q^2$+55q
Now that we have the pre-requisites, we find the profit function:
P(q) = R(q)-C(q)
P(q) = -$1.5q^2$+55q-(15q+200) = -$1.5q^2$+55q-15q-200
$\Rightarrow$ P(q) = -1.5$q^2$+40q-200
Break Even Cost
Setting P(q)=0, we get the quadratic equation in q:
1.5$q^2$-40q+200 = 0
With the quadratic formula at a=1.5, b=-40 and c=200, we get:
\[ q = \frac{-(-40) \pm \sqrt{(-40)^2-4(1.5)(200)}}{2(1.5)} \]
\[ q = \frac{40 \pm 20}{3} = \left( 20, 6.6667 \right) \]
Taking the smallest root as the solution:
No. of hats to break-even = 7
Maximizing Profits
For this, we first find P’(q), the derivative of the profit function:
\[ P’(q) = \frac{d}{dq}\left( -1.5q^2+40q-200 \right) = -3q + 40 \]
Note that this value is also the result of the calculator for the inputs “-1.5q^2+55q” and “15q+200” in the text boxes R(q) and C(q).
Setting P’(q)=0 to find the extrema:
\[ 40-3q = 0 \, \Rightarrow \, q = \frac{40}{3} = 13.333\ldots \]
no. of hats for maximum profit = 13
Thus, to obtain zero profit, at least seven fedoras must be manufactured. For maximum profit with the given model, no more or less than thirteen fedoras should be sold.
Let us verify this visually:
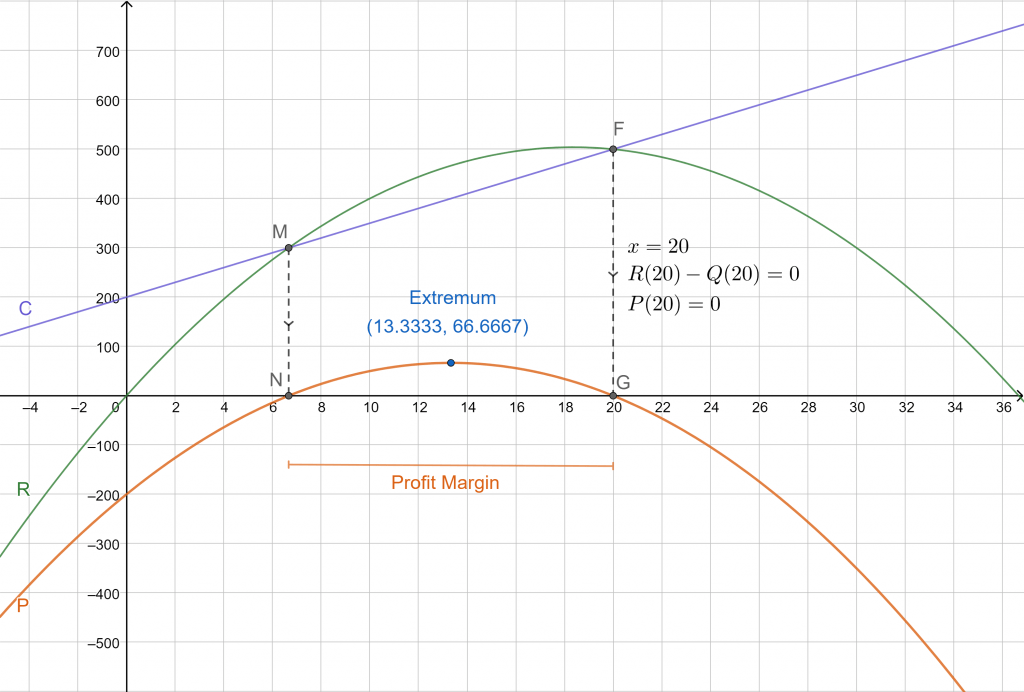
Figure 1
All graphs/images were drawn with GeoGebra.
