JUMP TO TOPIC
Quadratic Graph Calculator + Online Solver With Free Steps
The online Quadratic Graph Calculator is a calculator that helps you plot the graph of a quadratic equation. The Quadratic Graph Calculator is a powerful tool that helps students and professionals to plot and solve a complex quadratic equation quickly.
What Is a Quadratic Graph Calculator?
A Quadratic Graph Calculator is an online calculator that allows you to quickly plot complex quadratic functions irrespective of their complexity.The Quadratic Graph Calculator needs only one input; the quadratic equation of the graph. After inputting the quadratic equation, the Quadratic Graph Calculator instantly plots a graph when you click the “Submit” button.How To Use a Quadratic Graph Calculator?
To use the Quadratic Graph Calculator, you only need to plug in the input in its respective box and click the “Submit” button.The step-by-step instructions on how to use the Quadratic Graph Calculator are given below:Step 1
You first need to input the quadratic equation or function into the calculator.Step 2
After entering the quadratic equation into the calculator, click the “Submit” button. The Quadratic Graph Calculator will plot the graph of the equation and display it in a separate window.How Does a Quadratic Graph Calculator Work?
The Quadratic Graph Calculator works by using the quadratic equation as input and computing its graph. The calculator can also easily plot graphs for complex and higher degree polynomials.Quadratic equations used in the calculator must be similar to the following equation:\[ ax^{2}+bx+c=0 \tag*{(1)}\]What Are Quadratic Equations?
Quadratic equations are second-degree algebraic statements of the form given in equation (1). From the term “Quad,” which means square, comes the word “Quadratic.” A quadratic equation is a degree two equation, in other words.A second-degree algebraic equation in x is a quadratic equation. In equation (1), a and b are the coefficients, x is the variable, and c is the constant term. This is the quadratic equation in its standard form.The first requirement is the presence of a non-zero term in the coefficient of x$^\mathsf{2}$ i.e., a $\neq$ 0, which defines a quadratic equation. The x$^\mathsf{2}$ term is written first, then the x term, and finally, the constant term is written when constructing a quadratic equation in standard form. The numerical values of a, b, and c are typically expressed as integral values rather than fractions or decimals.Quadratic Formula
The quadratic formula is the most basic method for determining the solutions of a quadratic equation. Some quadratic equations are difficult to factor in; in these cases, we can quickly discover the roots using the quadratic formula. Finding the sum of the roots and the product of the roots of the quadratic equation is also made easier by using the roots of the equation. A single expression is used to represent the quadratic formula’s two roots. The two separate roots of the equation can also be obtained using the positive and negative signs.The following equation is a general representation of the quadratic formula:\[ ax^{2} + bx + c = 0 \]\[ x = \frac{-b \pm \sqrt{b^{2}-4ac}}{2a} \]What Are the Roots of a Quadratic Equation?
A quadratic equation’s roots are the two values of x obtained by solving the quadratic equation. The symbols alpha ($\alpha$) and beta ($\beta$) are used to denote a quadratic equation’s roots. The zeros in the equation are another name for these quadratic equation roots.Without actually locating the roots ($\alpha$, $\beta$) of the equation, the nature of the roots of a quadratic equation can be determined. We use the discriminant value, a component of the quadratic equation solution formula that is made achievable.The discriminant of a quadratic equation is denoted by the letter D and is equal to the value b$^\mathsf{2}$ – 4ac. It is possible to predict the nature of the quadratic equation’s roots based on the discriminant value.Solved Examples
The Quadratic Graph Calculator quickly provides a plotted graph of the quadratic equation you input into the calculator.Here are some examples of quadratic graphs solved using the Quadratic Graph Calculator:Example 1
While solving his assignment, a high school student needs to plot a graph using the following quadratic equation:\[ -x^{3}-2x^{2}+ 5x+25 \]Use the Quadratic Graph Calculator to plot the graph of the quadratic equations given above.Solution
We can easily use the Quadratic Graph Calculator to plot the graph for the given quadratic equations quickly. First, we enter the quadratic equation provided to us in the Quadratic Graph Calculator; the quadratic equation is -x$^\mathsf{3}$ – 2x$^\mathsf{2}$ + 5x + 25. After entering the quadratic equation in its respective box, we click the “Submit” button present on the Quadratic Graph Calculator. The calculator computes the results and displays the graph in a new window.The following results are extracted from the Quadratic Graph Calculator:Input Interpretation: plot $\boldsymbol{\rightarrow}$ –x$^\boldsymbol{\mathsf{3}}$ – 2x$^\boldsymbol{\mathsf{2}}$ + 5x + 25Plot: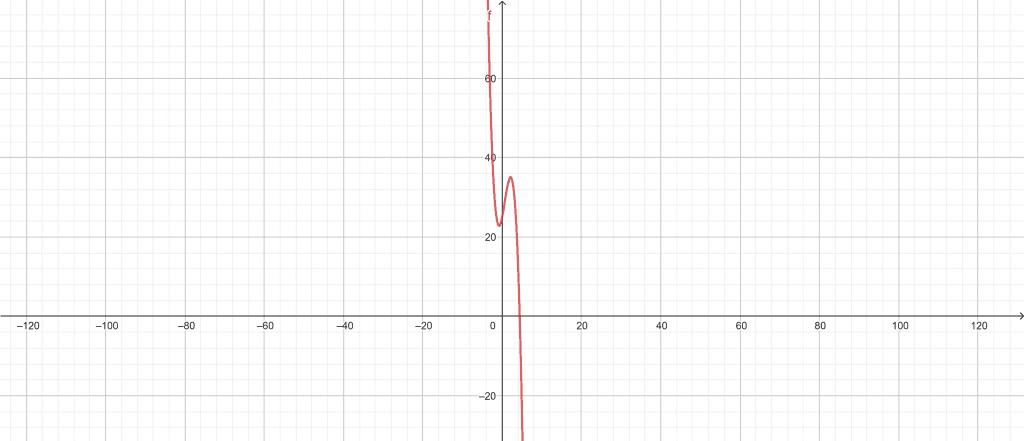
Figure 1
Example 2
During his research, a mathematician needs to plot the graph of a complex quadratic function. The equation is shown below: \[ 5x^{2}+2\sin{(x)}+6 \]Using the Quadratic Graph Calculator, plot the graph of the quadratic function given above.Solution
We can instantly use the Quadratic Graph Calculator to plot the graph of the quadratic equation given above. To use the calculator, we first need to plug the quadratic equation given to us in its respective box; the quadratic equation is 5x$^\mathsf{2}$ + 2sin(x) + 6. After adding the quadratic equation into the Quadratic Graph Calculator, we click the “Submit” button. The calculator will instantly plot a graph for the given quadratic equation.The following results are extracted from the Quadratic Graph Calculator:Input interpretation: plot $\boldsymbol{\rightarrow}$ 5x$^\boldsymbol{\mathsf{2}}$ + 2sin(x) + 6Plot: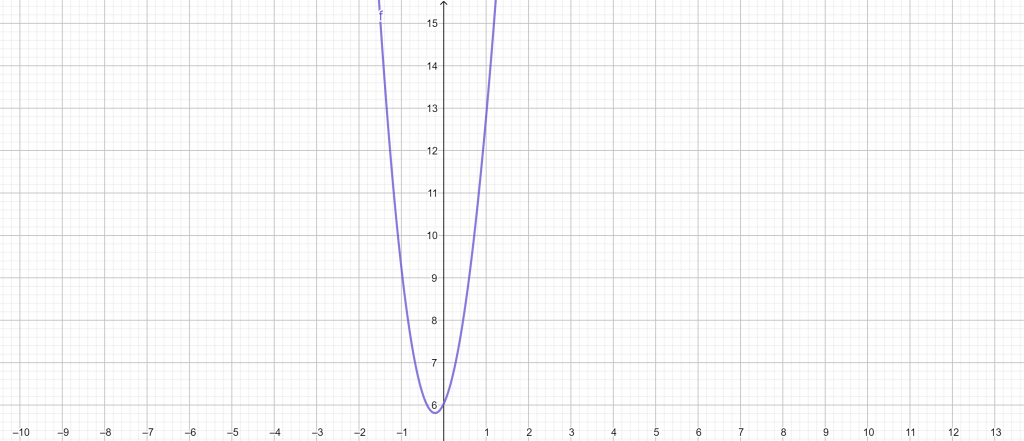
Figure 2
Example 3
Consider the following quadratic equation:\[ -7x^2+cos(2x)-4 \]Use the Quadratic Graph Calculator to plot a graph for the quadratic equations given.Solution
Using the Quadratic Graph Calculator, we can plot the graph easily. First, we enter the quadratic equation into the calculator. After entering the equation, we click the “Submit” button. The calculator will plot the graph and display it in a separate window.Here are the results derived from the Quadratic Graph Calculator:Input Interpretation: plot $\boldsymbol{\rightarrow}$ -7x$^\boldsymbol{\mathsf{2}}$ + cos(2x) – 4Plot: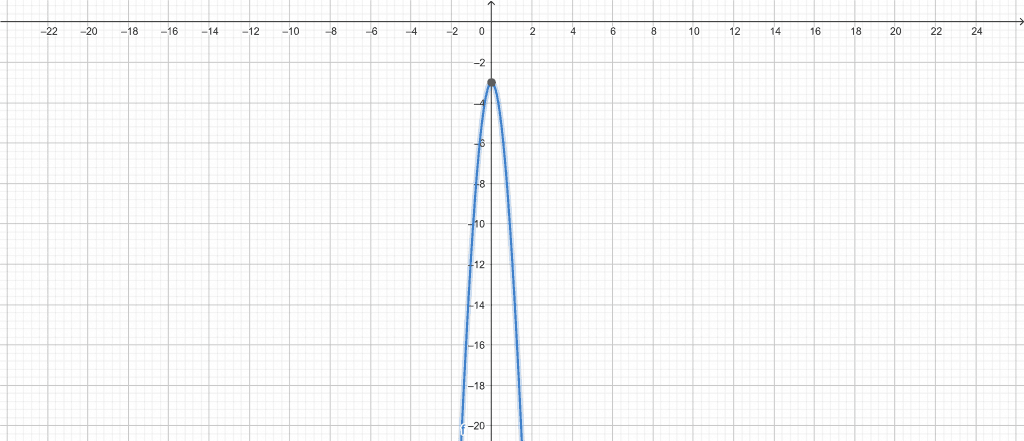
Figure 3
