JUMP TO TOPIC
Rearranging Equations Calculator + Online Solver With Free Steps
Rearranging Equations Calculator is also known as an Equation Solver Calculator. It can rearrange any kind of equation and gives the value of the desired variable in just a few seconds. All you have to do is to input the equation and you will get the results. The Rearranging Equations Calculator helps to solve all the algebraic equations, be it linear, quadratic, cubic, polynomial rational, exponential, and many more. It can also provide step-by-step solutions just by clicking the appropriate option given on the screen presenting the solution.
What Is a Rearranging Equations Calculator?
A Rearranging Equations Calculator is a calculator that is used to arrange the equation for an unknown variable so that its value can be determined. In other words, it can also be called an equation solver calculator. Rearranging Equations involves the modification of the equation to represent it in a different form to find the expression for the desired variable. For instance, the given equation a = b+ c can be rearranged in different ways depending upon the variable that needs to be addressed. For calculating b, the equation becomes b = c – a and for c, the equation becomes c = a – b. Therefore, an equation can be manipulated or rearranged to display it concerning a different subject. The variable of interest in an equation is referred to as a subject.How To Use the Rearranging Equation Calculator
The Rearranging Equation Calculator can be used by following the simple steps mentioned below. All you need to do is be aware of the equation to be solved and determine the changing subject of the equation.
Figure-1 Step by Step Re-Arranging Process
Step 1:
First of all, input the desired equation in the Equation tab.Step 2:
In the next step, you have to select the variable of choice or the subject which needs to be isolated on the one side of the equation.Input the variable in the Subject tab.Step 3:
Once you are done with the steps mentioned above, simply click the submit button.Step 4:
After clicking the submit button, a window will appear in front of you displaying the desired results. If you want to have a step-by-step solution, click the button “Need a step by step solution for this problem?” and you can view the detailed solution for the given problem.Step 5:
If you want to find the solution for any other equation, just simply change the Equation and Subject tab entries and keep solving as many equations as you want.What Is Rearranging Equations?
Rearranging Equations is a mathematical technique of manipulating the equation to solve it for the variable of interest. It involves rearranging the equation so that any other variable of interest becomes the subject, provided that both sides of the equality remain the same.Here are some steps involved in rearranging an equation:- Identify the variable in the equation that needs to be the subject.
- Segregate the subject on one side of the equation such that all other variables and constants are on the other side of the equation.
- Apply the “Inverse Operation” such that the subject is on one side of the equation.
Solved Examples
Here are some examples of rearranging equations using the Rearranging Equation Calculator.Example 1
Rearrange the following equation for variable c.\[ 2x^2 + 4cy + 5xc = 10 \]Solution
First, input the given equation in the calculator and specify the subject as c.It will show the following results:\[ c = \dfrac{-2(x^2 – 5)}{ 5x + 4y } \]Where:\[ 5x + 4y \neq{0} \]Hence, the above-mentioned equation has been solved for variable c.Example 2
Solve the given equation to make z as the subject:\[ \sqrt{4xyz + 12} = 12 \]Solution:
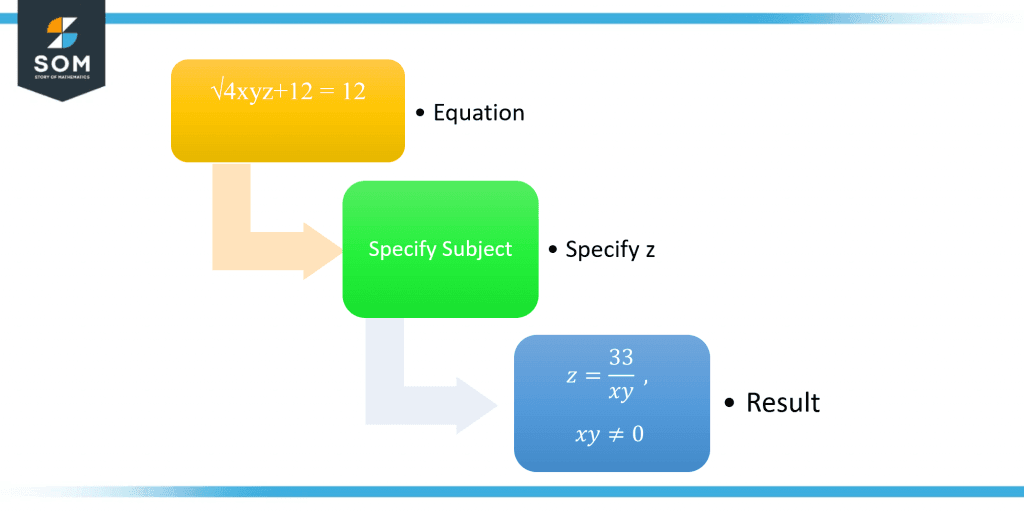
Figure-2 Solved Example 2
