Rectangular to Polar Equation Calculator + Online Solver With Free Steps

The Rectangular to Polar Equation calculator deals with two coordinate systems: the rectangular or the Cartesian Coordinate System and the Polar Coordinate System.

These two systems are used to determine the position of a point in a 2D plane. The Rectangular to Polar Equation calculator is used to determine the position of the point P(x,y) by finding the polar coordinates (r,θ).

What Is a Rectangular to Polar Equation Calculator?

A rectangular to polar equation calculator is an online calculator that converts two-dimensional rectangular coordinates into polar coordinates.

This calculator takes rectangular components x and y as input where x is the distance of a point P from the origin (0,0) along the x-axis and y is the distance of the point P from the origin along the y-axis.

The polar coordinates r and θ give the position of point P where r is the radius of the circle or the distance traveled from the center of the circle to the point P. θ is the angle from the positive x-axis in the counterclockwise direction.

Polar equation is given as:

\[ y = r (e)^{ι.θ} \]

It is obtained from the rectangular coordinate equation (x+ιy).

How To Use Rectangular to Polar Equation Calculator

Here are the steps required to use the rectangular to polar equation calculator.

Figure-2 Step by Step Conversion Method

Step 1:

Enter the x and y coordinate values against the blocks titled x and y respectively.

Step 2:

Press the submit button for the calculator to process the polar coordinates r and θ.

Output:

The output will show four windows as follows:

Input Interpretation:

The calculator shows the interpreted values for the x and y coordinates for which the polar coordinates are determined. The default values set for the x and y coordinates are 3 and -2, respectively.

Result:

The result block shows the values for r and θ. The value of r is obtained by putting the values of x and y in the following equation:

\[ r = \sqrt{ (x)^2 + (y)^2 } \]

The value of r shows the vector length or magnitude of the resultant vector which is always a positive value.

Also, the value of θ is obtained by putting the values of x and y in the following equation:

\[ \theta = \arctan (\frac{y}{x}) \]

The positive value of θ shows a counter-clockwise direction from the x-axis and the negative value shows a clockwise direction from the x-axis.

Vector Plot:

The vector plot shows a 2D graph with positive and negative x and y rectangular coordinate axes.

The resultant vector is drawn by the output polar vectors (r, θ) with magnitude r taken from the origin and angle θ taken from the positive x-axis. The quadrant of the resultant vector is determined by the (x,y) coordinates displayed on the plot.

Vector Length:

The vector length shows the magnitude r of the resultant vector.

Examples

Here are some examples that are solved using a Rectangular to Polar Equation Calculator.

Example 1:

For the rectangular coordinates

\[ (2, 2(\sqrt{3})) \]

find the polar coordinates (r,θ).

Solution:

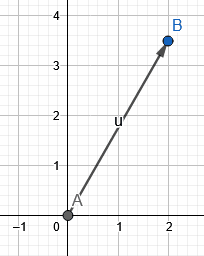
x = 2  and \[ y = 2(\sqrt{3}) \]

Putting the values of x and y in the equations of r and θ:

\[ r = \sqrt{ (x)^2 +(y)^2 } \]

\[ r = \sqrt{ (2)^2 + (2(\sqrt{3}))^2 } \]

\[ r = \sqrt{ 4 + 12 } \]

\[ r = \sqrt{ 16 } \]

r = 4 

\[ \theta = \arctan (\frac{y}{x}) \]

\[ \theta = \arctan (\frac{2(\sqrt{3})}{2}) \]

\[ \theta = \arctan ( \sqrt{3} ) \]

$\theta$ = 60° 

Figure 1 shows the resultant vector of example 1.

Figure 1

The same results are obtained using the calculator.

Example 2:

For the rectangular coordinates

\[ (-3(\sqrt{3}) , 3) \]

find the polar coordinates (r,θ).

Solution:

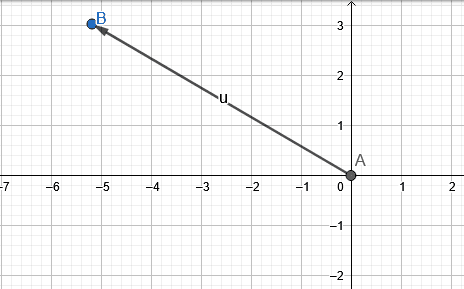
\[ x = -3(\sqrt{3}) \] and  y = 3 

Putting the values of x and y in the equation of r:

\[ r = \sqrt{ ( -3(\sqrt{3}) )^2 + ( 3 )^2 } \]

\[ r = \sqrt{ 27 + 9 } \]

\[ r = \sqrt{ 36 } \]

r = 6 

For the value of θ, ignoring the negative sign of 3(\sqrt{3}) for the reference angle Φ.

The result is shown as:

\[ \Phi= \arctan (\frac{3} {3(\sqrt{3}) }) \]

\[ \Phi = \arctan (\frac{1} {\sqrt{3}}) \]

$\Phi$ = -30° 

Adding 180° to Φ will give the angle θ.

The angle θ is given as:

\[ \theta = -30° + 180° \]

 $\theta$ = 150° 

Figure 2 shows the resultant vector for example 2.

Figure 2

The same results are obtained using the calculator.

Jacobian Matrix Calculator < Math Calculators List > Root Finder Calculator

All the images are created using GeoGebra.