JUMP TO TOPIC
Root Finder Calculator + Online Solver With Free Steps
The root finder calculator is used to find the roots of a polynomial of any degree greater than zero. The number of roots of the equation depends upon the degree of the polynomial.
This calculator takes the polynomial equation as input and provides all the possible solutions to the equation and plots the solution in a 2-D plane.

What Is a Root Finder Calculator?

Figure-1 Root Finder Calculator
A Root Finder Calculator is an online calculator that computes the roots or solutions of a function of nth degree where n = 1,2,3,4 and so on.
To explain its functioning, consider a quadratic function which is a second-degree polynomial written in the form \[ (p)x^2 + (q)x + r = 0 \] where p and $q$ are coefficients of (x)^2 and x, respectively, and r is a constant. If p = 0, the function becomes linear.
The roots of a quadratic equation are the x-intercepts of the function. The x-intercepts are obtained by putting the function y = f(x) = 0.
These points lie on the x-axis, giving the solutions of the function. This calculator can also find the x-intercepts of any polynomial with both real and imaginary roots.
How To Use the Root Finder Calculator
Here are the steps required to use the root finder calculator.
Step 1:
The calculator shows a quadratic equation of the form:
\[ (p)x^2 + (q)x + r = 0 \]
with p = 1, q = 3 and r = -7 set by default against the block titled “Find the roots of.”
Enter the quadratic equation of variable x with different values of p, q, and r for which the solution is required. The user can also incorporate higher-order equations of degrees greater than two depending on the requirement.
Step 2:
Click the Submit button after entering the polynomial. The calculator computes the roots of the function by putting it equal to zero.
Output:
The calculator processes the input equation which opens the following output windows.
Input Interpretation:
The calculator interprets the input polynomial and displays the equation for the user for which the roots are to be determined.
Results:
This window shows the roots or solutions for the equation. These are the x-intercepts with y = 0. These roots can be real or imaginary depending upon the discriminant value in the quadratic formula.
The quadratic formula for the quadratic equation:
\[ (p)x^2 + (q)x + r = 0 \]
is
\[ x = \frac{ -q \pm \sqrt{ q^2 – 4pr } } { 2p } \]
Here, the value of discriminant:
\[ D = q^2 – 4(p)(r) \]
determines the roots to be real or imaginary.

Figure-2 Decision Making About Roots
Root Plot:
The root plot shows the graph in the 2D plane for the input equation. The roots are represented by dots on the x-axis. The imaginary roots are displayed in the complex plane.
Number Line:
This window displays the roots of the equation on the number line.
Sum of Roots:
This window is displayed when there are numerous roots. The roots are added and their sum is obtained.
Product of Roots:
This window displays the product of all the roots by multiplying them simultaneously.
Solved Examples
Here are some examples that can be solved using the Root Finder calculator.
Example 1
Find the roots for the equation:
\[ x^2 + 4x – 7 \]
Solution
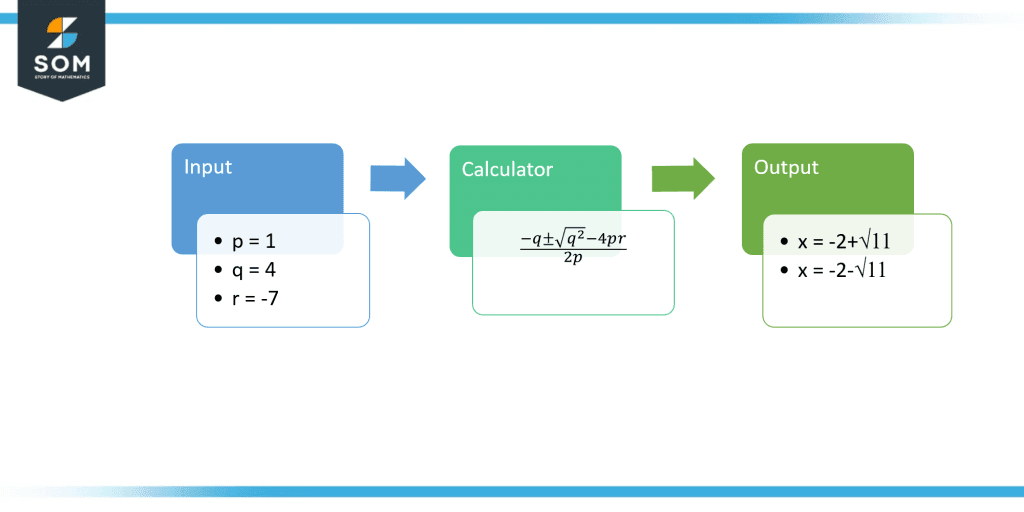
Figure-3 Solved Example
Using the equation:
\[ x^2 + 4x – 7 = 0 \]
Input the above-mentioned equation in the calculator.
The quadratic formula is used to find the roots of the quadratic equation:
\[ (p)x^2 + (q)x + r = 0 \]
The formula is given as:
\[ x = \frac{ -q \pm \sqrt{ q^2 – 4pr } } { 2p } \]
Step-wise solution of the problem is given as:
Here,
p = 1
q = 4
r = -7
\[ x = \frac{ -4 \pm \sqrt{ (4)^2 – 4(1)(-7) } } { 2(1) } \]
\[ x = \frac{ -4 \pm \sqrt{ 16 + 28 } } { 2 } \]
\[ x = \frac{ -4 \pm \sqrt{ 44 } } { 2 } \]
\[ x = \frac{ -4 \pm 2\sqrt{ 11 } } { 2 } \]
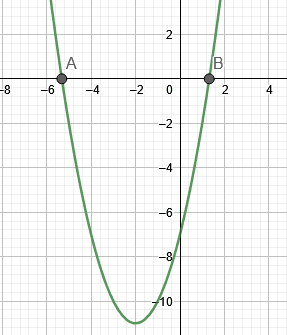
\[ x = -2 \pm \sqrt{ 11 } \]
So the roots are
\[ x = -2 + \sqrt{ 11 } , -2 – \sqrt{11} \]
Figure 1 shows the roots of example 1.
The sum of roots S is;
\[ S = (-2 + \sqrt{ 11 }) + (-2 – \sqrt{11}) \]
\[ S = (-2 -2) + ( \sqrt{ 11 } – \sqrt{11}) = -4 + 0 = -4 \]
And the product of roots P is:
\[ P = ( -2 + \sqrt{ 11 } )( -2 – \sqrt{11} ) \]
\[ P = 4 + 2\sqrt{ 11 } -2)\sqrt{ 11 } – 11 = 4 + 0 – 11 = -7 \]
The same results are obtained using the calculator.
Example 2
Find the roots for the equation:
\[ x^2 – 6x + 9 \]
Solution
Put the given equation in the calculator:
\[ x^2 – 6x + 9 = 0 \]
Quadratic formula is given as:
\[ x = \frac{ -q \pm \sqrt{ q^2 – 4pr } } { 2p } \]
Given that:
p = 1
q = -6
r = 9
Step-wise Solution is given below.
The formula becomes:
\[ x = \frac{ -(-6) \pm \sqrt{ (-6)^2 – 4(1)(9) } } { 2(1) } \]
\[ x = \frac{ 6 \pm \sqrt{ 36 – 36 } } { 2 } \]
\[ x = \frac{ 6 \pm \sqrt{ 0 } } { 2 } \]
\[ x = \frac{ 6 \pm 0 } { 2 } \]
\[ x = \frac{ 6 } { 2 } \]
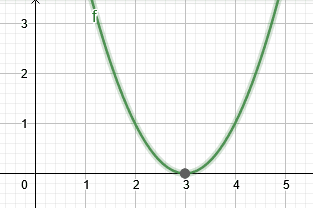
x = 3
So the root of the above equation is 3.
Figure 2 shows the root of example 2.
The same results are obtained using the calculator.
Example 3
Find the roots for the equation given below:
\[x^3 + 2x^2 – 5x -10\]
Solution
Input the following equation in the calculator to obtain the roots:
\[ x^3 + 2x^2 – 5x -10 = 0 \]
Step-wise Solution is given as:
Using the factorization method:
Take ( x + 2 ) as a common factor.
\[ x^2 ( x + 2 ) – 5 ( x +2 ) = 0\]
\[( x + 2 ) ( x^2 – 5 ) = 0\]
( x + 2 ) = 0
x = -2
\[ ( (x)^2 – 5 ) = 0\]
\[(x)^2 = 5\]
\[ \sqrt{x^2} = \sqrt{5}\]
\[ x = \pm \sqrt{5}\]
So the roots are
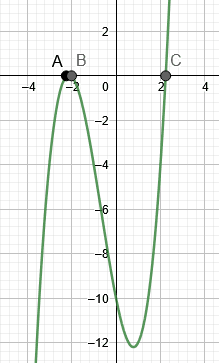
x = -2
\[\sqrt{5} \]
\[-\sqrt{5} \]
Figure 3 shows the roots of example 3.
The sum of roots S is:
\[ S= -2 + \sqrt{5} + (-\sqrt{5}) = -2 + 0 = -2 \]
The product of roots P is:
\[ P = (-2) (\sqrt{5}) (-\sqrt{5}) = 2(5) = 10 \]
The same results are obtained using the calculator.
Rectangular To Polar Equation Calculator < Math Calculators List > Net Ionic Equation Calculator
All the images are created using GeoGebra.