JUMP TO TOPIC
Sequence Formula Calculator + Online Solver With Free Steps
The Sequence Formula Calculator is an online widget that is used to find upcoming terms of a sequence and the general form of the sequence. This calculator has a user-friendly layout that prompts users to enter initial terms and view the results.
An arrangement of numbers in a specific order is called a sequence. In sequence, the position of each element matters and it allows repetition of the numbers.
The calculator presents a general representation, the expansion, and plots a graph of the given sequence.

What Is a Sequence Formula Calculator?
A Sequence Formula Calculator is an online tool that is designed to determine an appropriate formula for your sequence-related problems.
Almost every process in the world follows some pattern. It can be observed anywhere like in the rotation of the clock or some complex statistical problems. All such processes come under the shed of sequence.
Therefore it is very important to find general forms for the various sequences that occur in real-life problems. Finding a formula for any sequence is not a difficult task, but one needs to extract the pattern that each element follows the list.
It can be found by observing the difference between two consecutive terms and repeating this process for all of the terms.
It takes a lot of time and computational resources to determine the formula of an unknown sequence. But the Sequence Formula Calculator has made this process super easy for you. You just have to place terms and it will quickly solve your problem.
Another benefit of this calculator is that you can use it anytime and anywhere. Also, the simple front end of the calculator makes it very easy to comprehend how it works. The calculator is extremely efficient and reliable as it gives fast and perfect results.
How To Use the Sequence Formula Calculator?
You can use the Sequence Formula Calculator by inserting several sequences in the given boxes. It allows only to enter the first five values of the sequence.
It can be any type of sequence whether a specific sequence like geometric or arithmetic sequence and it can be some common sequence like prime numbers. The procedure to use this calculator consist of the following steps:
Step 1
First, select a problem you want to solve with sequence. Put the first and second values of the problem in the 1st term and 2nd term fields respectively.
Step 2
Similarly, enter the numbers present in third and fourth place of the list in the 3rd term and 4th term boxes respectively.
Step 3
Now insert the fifth value in the fifth term tab. As you have entered all the required terms press the Solve button to get the answer.
Result
The solution is expressed in multiple sections. It starts by presenting the input interpretation. Then it displays the possible sequence identification if any for example it resembles a sequence of some chess piece.
Then it displays a formula in the Closed-Form section. This formula is a general form of the entire sequence. It is a function of $n$ which denotes the number of terms. You can find the value of any term just by putting the value of its respective n.
Also, it continues the sequence by giving the remaining terms of the sequence. By default, it represents a few remaining terms but you can view more terms by selecting the option of “More.”
Lastly, it gives the plot which helps you to graphically visualize your sequence. The graph displays the values of the sequence against each term number.
How Does the Sequence Formula Calculator Work?
The Sequence Formula Calculator works by obtaining the common relationship between every two consecutive terms of the sequence, then it represents this relationship in a mathematical form which valid for the whole sequence.
To develop a better understanding of the working of the calculator we need to explore some core concepts. Here is a brief discussion about each concept.
What Is a Sequence?
A sequence is the placement of several things in a particular specified pattern or order. There are two types of sequence. The Finite sequence has a definite amount of terms while the Infinite sequence means a never-ending set of numbers.
The order matters a lot in such a sequence as increasing or decreasing numbers. If any two consecutive terms of a set don’t have a common relation then it cannot be said as a sequence.
The general form of the sequence is:
a1, a2, a3, … an
There are some special sequences which are explained below:
Arithmetic Sequence
In an arithmetic sequence, the difference between two adjacent terms is constant. For example, a list of numbers with a constant difference is 2. The general form of an arithmetic sequence is given as:
a, a+d , a+2d, …
The formula to calculate the value of any term is:
an = a + (n-1) d
Where $a$ is the first term, n is no of term and d is a common difference.
Geometric Sequence
In a geometric sequence, the consecutive terms are multiples of each other. For example the table of number 3. The general form of a geometric sequence is:
\[ \{ a, ar , a^{2}, … \} \]
The formula to find value of term is:
\[ a_{n} = ar^{n-1} \]
Where a is the first term and r is the common ratio.
Fibonacci Sequence
In the Fibonacci sequence, each term is the sum of its previous two terms. The formula to calculate the value of each term is:
an = a(n-1) + a(n-2)
Solved Examples
Let’s solve some mathematical problems using the Sequence Formula Calculator.
Example 1
A college student in a maths exam is given the following sequence:
( -4, 1, 6, 11, 16 )
The student is asked to find a generic formula for sequence and find out the next values in sequence.
Solution
The answer for the given problem by the calculator is given as:
Closed-Form
The general formula for the sequence is as follows:
an = 5n – 9
Continuation
The next terms after the first five are given below:
-4, 1, 6, 11, 16, 21, 26, 31, 41, 46, 51, 56, 61, 66, 71, 76, 81, …
Plot
The graph of the sequence is given in figure 1. The y-axis represents values of terms an whereas the x-axis denotes the number n of the term.
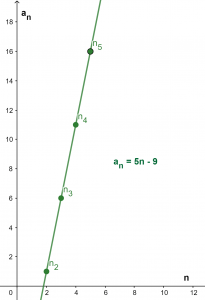
Figure 1
Example 2
Consider the following sequence:
\[ \left( \frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \frac{1}{243} \right) \]
Completely solve the sequence and derive the formula using Sequence Formula Calculator.
Solution
The solution to the problem is divided into three sections. Each of the sections is described below:
Closed-Form
The formula for the provided fractional sequence is:
\[ a_{n} = 3^{-n} \]
Continuation
The continuation of the sequence by the calculator is as follows:
\[ \frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \frac{1}{243}, \frac{1}{729}, \frac{1}{2187}, \frac{1}{6561}, \frac{1}{19683}, \frac{1}{59049}… \]
Plot
The graph of the sequence is illustrated in figure 2.
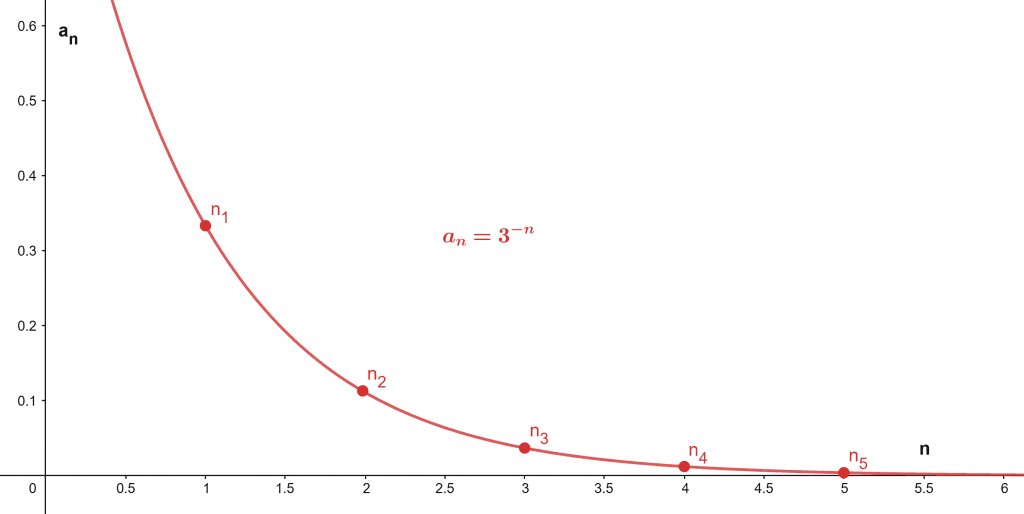
Figure 2
All the Mathematical Images/Graphs are created using GeoGebra.
