JUMP TO TOPIC
Standard Form Calculator + Online Solver With Free Steps
The online Standard Form Calculator is a calculator that uses the input values and creates the standard form equation.
The Standard Form Calculator is a powerful tool that helps scientists and mathematicians quickly determine the standard form of an equation.

What Is a Standard Form Calculator?
The Standard Form Calculator is an online tool that allows you to find the standard form equation for the given inputs.
The Standard Form Calculator needs four inputs to operate: the coefficient for X, the coefficient for Y, the operator symbol, and the right side of the equation.
After adding all the inputs into the Standard Form Calculator, we click the “Submit” button. The results are calculated almost instantaneously.
How To Use a Standard Form Calculator?
We can use the Standard Form Calculator by adding the required inputs and clicking the “Submit” button.
The detailed instructions on how to use the Standard Form Calculator can be seen below:
Step 1
First, we must add the coefficient of X into the Standard Form Calculator.
Step 2
After adding the coefficient of X, we enter the coefficient of Y into the Standard Form Calculator.
Step 3
We add the operator symbol to let the calculator know what operation we wish to perform. We add the operator symbol after entering the coefficient of Y.
Step 4
After inputting the operator symbol, we enter the right side of the equation into the Standard From Calculator.
Step 5
Finally, after entering all the inputs in the Standard Form Calculator, we click the “Submit” button. The calculator quickly calculates the results and displays them in a new window. The results include a standard form of the equation, a plotted diagram, and other details about the equation.
How Does a Standard Form Calculator Work?
The Standard Form Calculator works by taking in the inputs and arranging them according to the standard form of the equation. The standard form equation is a general way of representing the equation. The following is an example of a standard form equation:
ax + by = c
Standard Form Equation
The standard form equation is the most general manner of representing any type of equation. The standard form formula represents the frequently accepted form of an equation, which is a common form of an equation.
For example, in the standard form of a polynomial, the terms with the highest degree are written first (descending order of degree), and the coefficients must be in integral form. As a result, the standard form formula aids in presenting the general representation for many types of notation.
The standard form formula is represented by a formula based on the degree of the equations. The following examples represent the standard form of an equation:
ax + by = c (Standard form equation)
\[ a^{2}x + bx + c = 0 \ \text{(Standard form of quadratic equation)} \]
An equation’s basic form is the standard form of a linear equation. In this case, x and y are variables, and a and b are coefficients.
In contrast, a quadratic equation in its standard form is a second-degree equation with a variable, coefficients, and a constant term. It is a single variable of degree 2 in this case.
Standard Form of a Linear Equation
The standard form of linear equations is a method of writing linear equations. A linear equation can be expressed in several ways, including the standard form, the slope-intercept form, and the point-slope form. The standard form of linear equations, often known as the general form, is expressed as Ax + By = C.
A linear equation, often known as a one-degree equation, is one in which the maximum power of the variable is 1. For example, 2x + y = 8 is a linear equation since the maximum power of both variables x and y are 1. The conventional form of a linear equation is: Ax + By = C, where A, B, and C are integers and x and y are variables.
Standard Form of Linear Equations in Single Variable
A linear equation in a single variable denotes an equation with only one variable. This means that there is just one solution to this linear equation. The standard or generic form of linear equations in one variable is written as follows:
Ax + B = 0
Where:
A and B = integers
x = single variable
4x + 3 = 0 is an example of the standard form of linear equation in a single variable.
Standard Form of Linear Equations in Two Variables
A linear equation with two variables has two solutions. The standard form of linear equations (generic form of linear equations) in two variables is written as:
Ax + By = 0
Where:
A and B = integers
x and y = variables
2x + 3y = 0 is an example of a standard form of linear equations in two variables.
Solved Examples
We can use the Standard Form Calculator by entering the required input information and clicking the “Submit” button. The calculator will display the results quickly.
Here are some examples solved using the Standard Form Calculator:
Example 1
While working on his assignment, a college student needs to find the standard form of an equation. The student was given the following inputs:
A = 3
B = 2
C = 2
The operation to be performed = subtraction
Using the Standard Form Calculator, find the standard form of the equation using the inputs given.
Solution
We can use the Standard Form Calculator to calculate the standard form equation. First, we enter the coefficient value of X in the Standard Form Calculator; the coefficient value is 3. After entering the coefficient value of X, we enter the operation symbol we want to perform; in this case, we subtract, so we use $-$. After entering the operation symbol, we enter the coefficient value of Y in its respective box; the coefficient value of Y is 2. Once you add the coefficient value of Y, we can enter the value of C; the value of C is 2.
Finally, when all the inputs are entered into the Standard Form Calculator, we click the “Submit” button. The calculator displays the equation’s standard form and a graph in a new window.
The following results are generated using the Standard Form Calculator:
Input:
3x – 2y = 2
Geometric Figure:
Line
Implicit Plot:
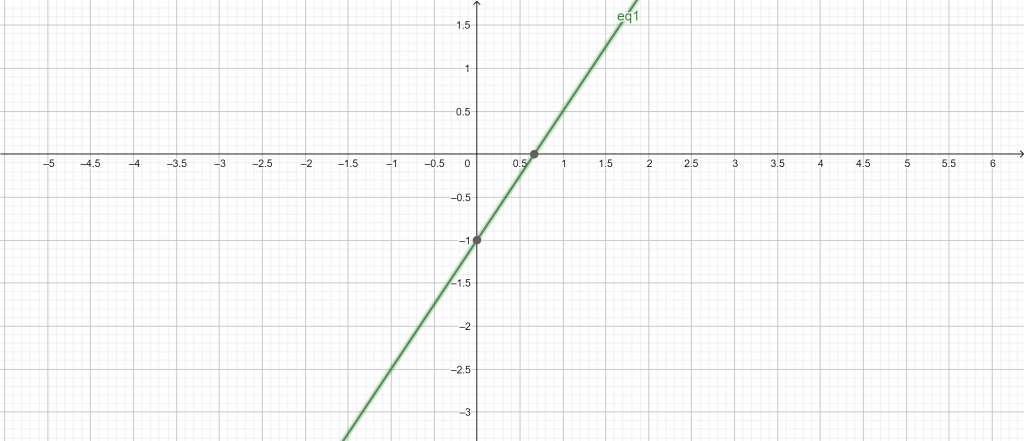
Figure 1
Alternate Forms:
\[ y = \frac{3x}{2}-1 \]
3x -2y – 2 = 0
3x = 2(y + 1)
Real Solution:
\[ y = \frac{3x}{2}-1 \]
Solution:
\[ y = \frac{3x}{2}-1 \]
Integer Solution:
x = 2n, y = 3n – 1, n $\in$ Z
Solution for variable y:
\[ y = \frac{1}{2} (3x – 2) \]
Example 2
While conducting his research, a mathematician needs to find the standard form equation of the following values:
A = 4
B = 21
C = 3
The operation to be performed = multiplication
Using the Standard Form Calculator, find the standard form equation of the given values.
Solution
The Standard Form Calculator can be used to compute the standard form equation. First, we enter the coefficient value of X into the Standard Form Calculator; it is 4. We insert the operation symbol we wish to do after entering the coefficient value of X; in this case, we multiply, so we use $*$. Following the operation symbol, we input the coefficient value of Y in the appropriate box; the coefficient value of Y is 21. We can enter the value of C after adding the coefficient value of Y; the value of C is 3.
Finally, after entering all of the inputs into the Standard Form Calculator, we click the “Submit” button. The calculator displays the equation’s standard form and a graph in a new window.
The Standard Form Calculator yields the following results:
Input:
4x $\times$ 21y = 3
Results:
84xy = 3
Implicit Plot:
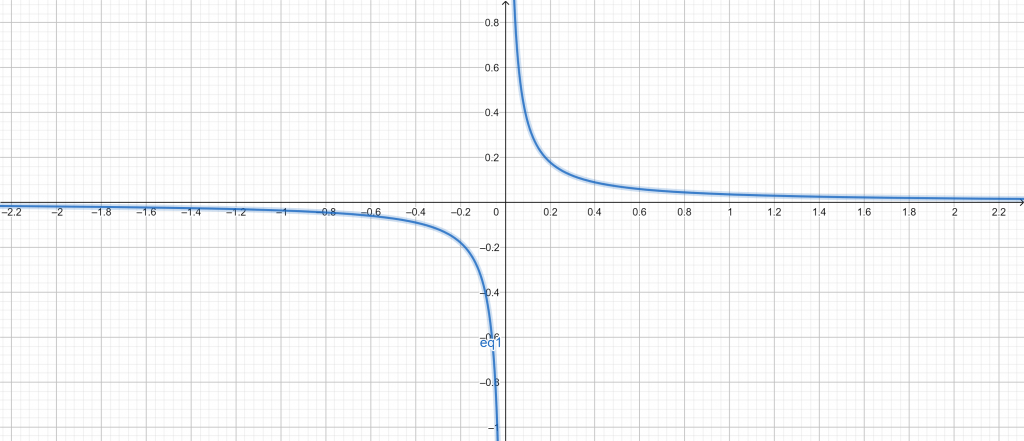
Figure 2
Solution:
\[ x \neq 0, \ y = \frac{1}{28x} \]
Example 3
Consider the following values:
A = 5
B = 34
C = 4
The operation to be performed = addition
Using the Standard Form Calculator, find the standard form equation using the input given to us.
Solution
To compute the standard form equation, use the Standard Form Calculator. First, we enter the value of X’s coefficient into the Standard Form Calculator, which is 5. After inputting the coefficient value of X, we insert the operation symbol we want to accomplish; in this case, we want to add, so we use $+$. We enter the coefficient value of Y in the relevant field after we enter the operation symbol; the coefficient value of Y is 34. After adding the Y coefficient value, we may input the value of C, which is 4.
Finally, we click the “Submit” button after inputting all data into the Standard Form Calculator. The calculator displays the equation’s standard form and a graph in a new window.
The Standard Form Calculator produces the following outcomes:
Input:
5x + 34y = 4
Geometric Figure:
Line
Implicit Plot:
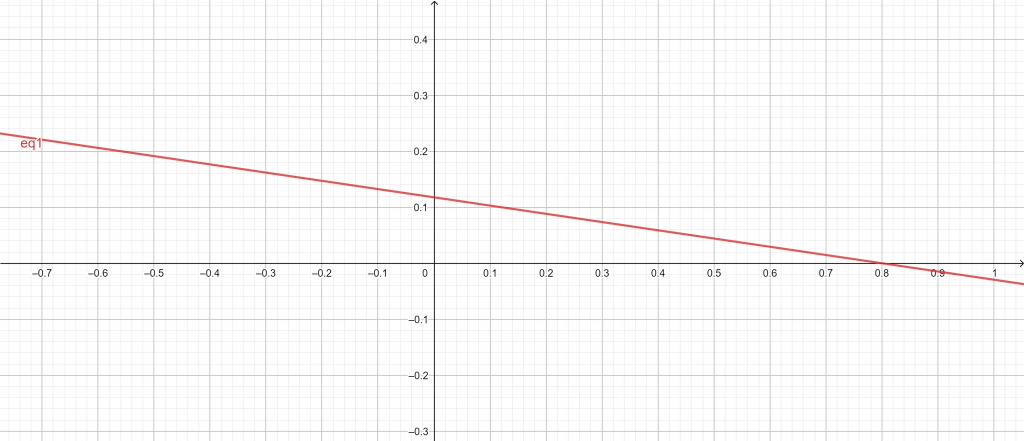
Figure 3
Alternate forms:
\[ y = \frac{2}{17}-\frac{5x}{34} \]
5x + 34y – 4 = 0
Real Solution:
\[ y = \frac{2}{17}-\frac{5x}{34} \]
Solution:
\[ y = \frac{2}{17}-\frac{5x}{34} \]
Integer Solution:
x = 34n + 28, y = -5n – 4 , n $\in$ Z
Solution for the variable y:
\[ y = \frac{1}{34}(4-5x) \]
All Images/Graphs are drawn using GeoGebra.
