JUMP TO TOPIC
Transformations Calculator + Online Solver With Free Steps
The Transformations Calculator computes the Laplace Transform F(s) = L{f(t)} of the given function of time f(t). The calculator supports multi-variable functions but performs the transformation only on the time variable ‘t.’
The Laplace Transform takes a function in the time domain and converts it to the frequency (s is a complex number) domain. This domain transformation greatly simplifies some otherwise complex differential analyses/equations in the time domain.
The Laplace transform is ubiquitous in many fields of mathematics and engineering.

What Is the Transformations Calculator?
The Transformations Calculator is an online tool that finds the Laplace Transform of any given function in the time domain and presents the result in the frequency domain.
The calculator interface contains a single text box labeled “Laplace Transform.” Here, you must enter your expression as a function of time. The calculator will then convert it to the Laplace (frequency) domain.
How To Use the Transformations Calculator?
You can use the Transformations Calculator to find the Laplace transform of any given function in the time domain by simply entering that function.
As an example, consider you want to find the Laplace Transform of the following exponential:
\[ f(t) = e^{-at} \]
You can use the calculator to do so by following the step-by-step guidelines below:
Step 1
Make sure your function is a function of time. In our example, we have the variable ‘t’ in our function, so we skip this step.
If your function has multiple variables, time should be termed ‘t.’ Otherwise, the calculator assumes the variable letter earlier in alphabetical order to represent time. For example, in $e^{yx}$, x is considered the time variable and does not appear in the result.
Step 2
Enter the function of time into the text box. In our example, we would enter “e^(-at).”
Step 3
Press the Submit button to get the results.
Results
The results open in a new window and span several sections.
The immediately relevant (main) results show in the following sections:
- Input Interpretation: This section contains the input as interpreted by the calculator. You can use this for manual verification and adjust accordingly for errors.
- Result: The function in the Laplace/frequency/s domain.
- 2D/3D Plot: If the input function was purely a function of time, a 2D plot appears in this section. If there are a maximum of two variables (including time), this is a 3D plot. For more than two variables, this section does not appear.
Several other sections contain extra information on the s-domain result. These include the derivative, the indefinite integral, and the limit as s $\to \infty$. They can be helpful in some cases.
How Does the Transformations Calculator Work?
The Transformations Calculator works by solving the following improper integral defining the Laplace Transform:
\[ F(s) = \mathcal{L} \{ f(t) \} = \int_0^\infty e^{-st}f(t)dt \tag*{(1)} \]
In the above equation, for a complete transformation of domains, s has the inverse unit of time, i.e., frequency. $e^{-st}$ is often called the kernel function and is dimensionally inert (s and t dimensions cancel out).
It is possible to relate s to the complex plane using the idea of rotating phasors (imaginary part $i\omega$) and a decay factor (real part $\sigma$), leading to s = $\sigma$ + $i\omega$.
The integral of is evaluated from 0 to $\infty$ because, in this particular range, we end up with no mention of the time variable in the final result, thereby transforming the differential equation into an algebraic one!
In the case of multivariable functions, depending on the values of s and the other variables, we sometimes end up with diverging results. Therefore, it is better to define for which values the function converges and for which it diverges.
Solved Examples
Example 1
Consider the exponential function of time f(t) = $e^{at}$. Find its Laplace Transform for t $\geq$ 0. When will it be convergent? When will it be divergent?
Solution
Using equation (1), let us find the Laplace Transform for the given function:
\[ F(s) = \mathcal{L} \left\{ e^{at} \right\} = \int_0^\infty e^{-st} \cdot e^{at}dt \]
Given that $a^b \times a^c = a^{b+c}$, we get:
\[ F(s) = \int_0^\infty e^{(at-st)}dt \]
\[ F(s) = \int_0^\infty e^{t(a-s)}dt \]
Since $\int_a^b e^{nx} dx = \frac{1}{n}e^{nx}$, we apply it to get:
\[ F(s) = \left. \frac{e^{t(a-s)}}{a-s} \right\rvert_0^\infty \tag*{(2)} \]
Since we have the improper integral to infinity, we need to decide if the result is divergent or convergent. To do this, note that we have two variables that define the behavior, s and a. Let us consider the three possibilities:
Case 1: s = a
For this case, the numerator in equation (2) becomes 1 while the denominator becomes 0. Since division by zero is undefined, there is a singularity at this point, and F(s) consequently diverges.
Case 2: s < a
For this case, recognize that the term “a – s” remains positive. Essentially, the numerator is then a positive exponential $e^{pt}$, where p = a – s > 0 such that p($\infty$) = $\infty$. Therefore:
\[ F(s) = \left. \frac{e^{pt}}{p} \right \rvert_0^\infty \]
\[ F(s) = \frac{e^{p(\infty)}}{p}-\frac{e^{p(0)}}{p} = \frac{\infty}{p}-\frac{1}{p} = \infty-\frac{1}{p} = \infty \]
Therefore, F(s) is divergent in this case as well.
Case 3: s > a
Conversely to case 2, the term “a – s” will now always be negative. Assuming n = a – s < 0 such that n($\infty$) = $-\infty$, we extend equation (2) to get:
\[ F(s) = \left. \frac{e^{nt}}{n} \right \rvert_0^\infty \]
\[ F(s) = \frac{e^{n(\infty)}}{n}-\frac{e^{n(0)}}{n} = \frac{e^{-\infty}}{n}-\frac{1}{n} \]
Since $e^{-\infty} = \frac{1}{e^\infty}$ and we know that $e^\infty = \infty$. Therefore, we can see that $e^{-\infty} = \frac{1}{\infty} = 0$, leading to:
\[ F(s) = \frac{0}{n}-\frac{1}{n} = 0-\frac{1}{a-s} = \boldsymbol{\frac{1}{s-a}} \]
Thus, F(s) is convergent in this case.
The plots of F(s) are given below:

Figure 1
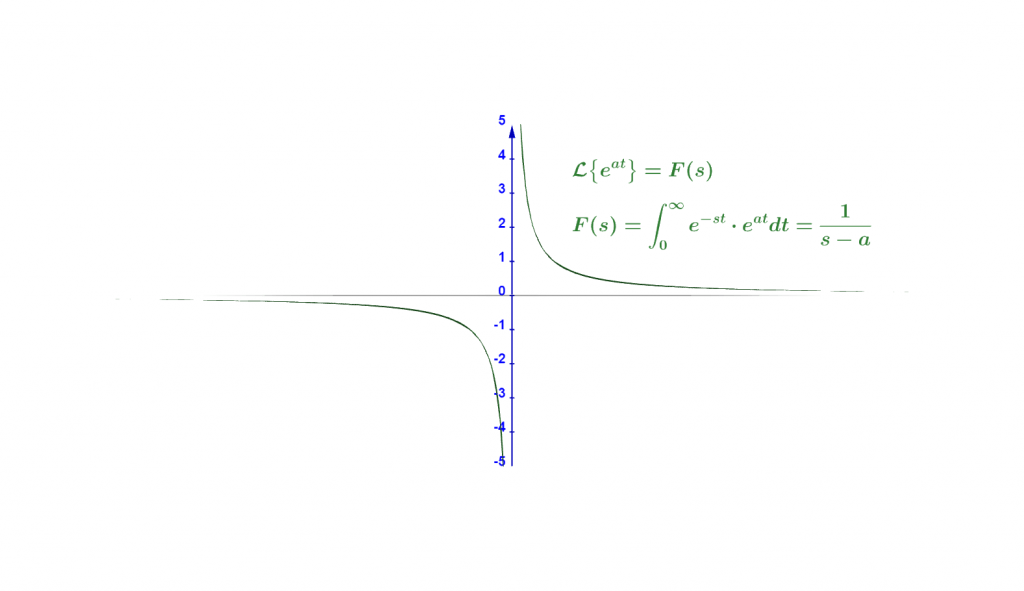
Figure 2
All graphs/images were created with GeoGebra.
