JUMP TO TOPIC
Mixed Fraction|Definition & Meaning
Definition
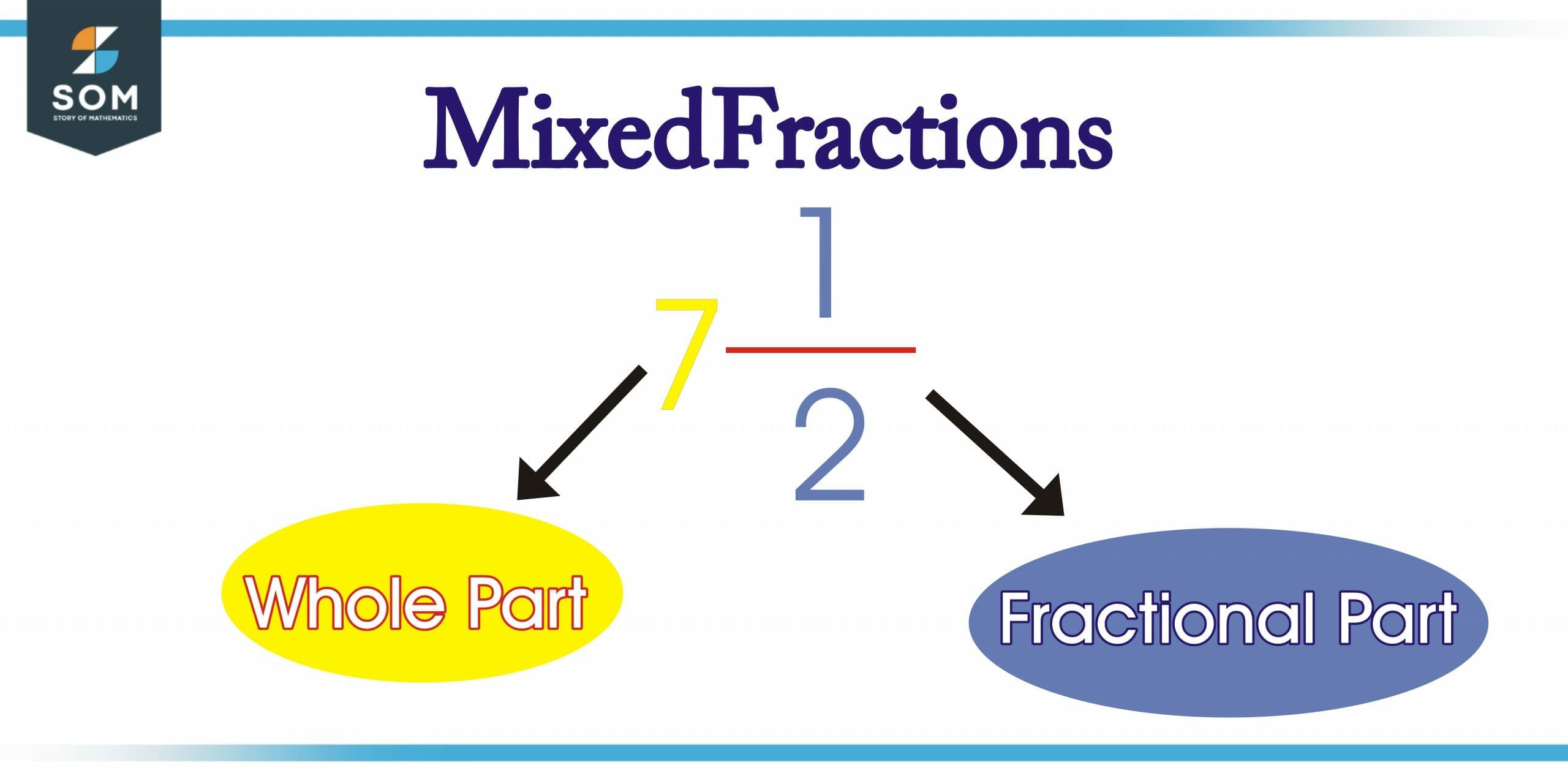
Mixed Fractions are fractions that have a whole part and a fractional part, both at the same time. These mixed fractions represent the quotient and remainder of a fraction.
The fractional part of mixed fractions is always a proper fraction. These are also known as Mixed Numbers. 4½ is an example of a mixed fraction. The term fraction refers to a portion of a whole. So, if we need to read a fraction 5/6, it is read as five-sixth of a whole. Similarly, we read the following fractions as:
2/4: two-fourth of whole
9/10: nine-tenth of whole
Figure 1 – Labeled Diagram of Mixed Fraction
How To Convert an Improper Fraction to a Mixed Fraction?
The improper fraction is a type of fraction in which a numerator is greater than or equal to the denominator and the resultant product cannot be simplified further. The following steps can be used to convert this improper fraction into a mixed fraction.
- The first step involves dividing the numerator by the denominator
- Calculate the remainder.
- The third step is the arrangement of the numbers in the order in which the quotient is followed by the remainder/divisor fraction.
For example, 11/5 is an improper fraction. This improper fraction can be converted into a mixed fraction by following the steps mentioned above. The resultant will be .
Mixed Fractions and Improper Fractions
Mixed fractions can also be converted to improper fractions. Follow the steps below to do that.
- The first step involves the multiplication of the denominator of a mixed fraction by the whole number part.
- Then the numerator is added to the product obtained from step 1.
- In the final step, the improper fraction is written in numerator/denominator form using the sum from step 2.
For example:
- Multiply 3 and 5 the product is 15.
- Then, add the product (15) with the numerator (2)
(15+2) = 17
- The resultant 17/5 is an improper fraction.
Let us take another example:
(3+2) = 5
The resultant product, in this case, is 5/3.
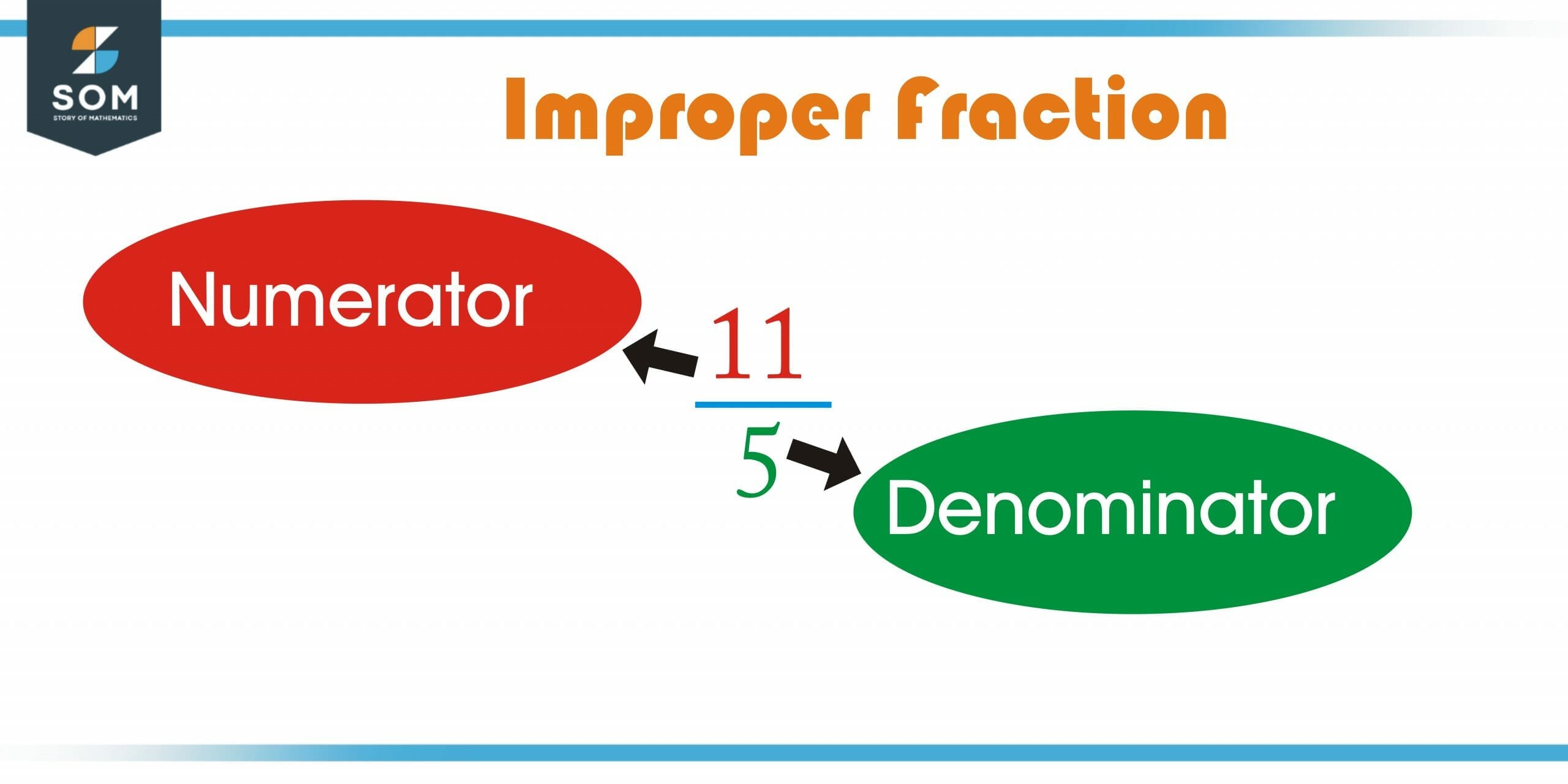
Figure 2 – Representation of an Improper Fraction
Performing Operations on Mixed Fractions
Arithmetic operations can also be applied to mixed fractions, just as we add, subtract, multiply, and divide numbers.
Mixed Fraction Addition
Following are the steps for adding mixed fractions:
- In the first step, the mixed fraction is converted to an improper fraction.
- Determine whether the denominators of the improper fractions are the same or not.
- In the third step, the numerators of the fractions are added.
- Determine the LCM of the denominators if they are not the same.
- To get the result of the addition we need to add the numerators together.
Consider the following example: add 2 1/2 and 3 1/2.
When these fractions are converted into an improper fraction, we get 5/2 and 7/2.
Adding 5/2 and 7/2, we get 12/2, and on further simplifying, we get 6.
Similarly, when 3 1/3 is added into 1 2/3, we get 15/3. When 15/3 is simplified further, we get 6.
Mixed Fraction Subtraction
Follow the steps below to subtract mixed fractions:
- Make improper fractions from mixed fractions.
- Determine whether the denominators are the same or not.
- If the denominators are the same, write down the result by subtracting the numerators.
- Determine the LCM of the denominators if they are not the same.
- The final result is obtained by subtracting the numerators
For example, when subtracted from the final result will be 2/2 which on further simplification gives us 1.
Mixed Fractions Multiplication
Following are the steps for multiplying mixed fractions:
- In the first step, the mixed fraction is converted to an improper fraction.
- The second step involves the multiplication of the numerator with the denominator and numerator.
- The result that is obtained can either be simplified to its simplest possible form, converted into a mixed fraction, or left as an improper fraction.
For example, multiply 1 1/2 and 3 1/2.
By converting the fraction into an improper fraction, we get 3/2 and 7/2.
On multiplying 3/2 and 7/2, we get 21/4.
Converting 21/4 to a mixed fraction, we get 5 1/4.
Mixed Fractions Division
Following are the steps for the division of mixed fractions:
- The First step is to convert the mixed fractions into improper fractions.
- In the second step, the multiplication inverse of the second fraction is multiplied by the first fraction.
- The result that is obtained can either be simplified to its simplest possible form, converted into a mixed fraction, or left as an improper fraction.
For example:
Let us divide 2 1/3 by 5 1/3.
By converting the fraction into an improper fraction we get 7/3 and 16/3.
On rearranging 7/3 and 16/3, we get 7/3 and 3/16, which is equal to 7/16.
What Are Mixed Equivalent Fractions?
When two fractions, such as 1/2 and 2/4, are reduced to their simplest forms, they are said to be equivalent. Similarly, when 6/18 and 7/24 are converted to mixed fractions are equivalent. Hence, when we divide the numerator by the denominator, the quotient left should be the same when converting any two equivalent fractions into mixed fractions.
For example, when 8/32 and 4/16 are converted to mixed fractions are equivalent.
Similarly, when we 5/4 convert to a mixed fraction, we get 1 1/4, and when we convert 10/8 into a mixed fraction, we get 1 1/4 which are equivalent.
Solved Examples for Mixed Fractions
Example 1: When Denominators Are the Same
| Mixed Fractions | Addition | Multiplication | Subtraction | Division |
| 2 1/2, 1 1/2 | 5/2 + 3/2 = 8/2 = 4 | 5/2 × 3/2 = 15/4 | 5/2 – 3/2 = 2/2 = 1 | 5/2 × 2/3 = 5/3 |
| 3 1/2, 2 1/2 | 7/2 + 5/2 = 12/2 = 6 | 7/2 × 5/2 = 35/2 | 7/2 – 5/2 = 2/2 = 1 | 7/2 × 2/5 = 7/5 |
| 2 1/5, 1 1/5 | 11/5 + 6/5 = 17/5 | 11/5 × 6/5 = 66/5 | 11/5 – 6/5 = 5/5 = 1 | 11/5 × 5/6 = 11/6 |
| 5 1/4, 2 1/4 | 21/4 + 9/4 = 30/4 = 7 | 21/4 × 9/4 = 189/4 = 46 | 21/4 – 9/4 = 12/4 = 3 | 21/4 × 4/9 = 21/9 |
| 2 1/5, 4 1/5 | 21/5 + 11/5 = 32/5 = 6 | 21/5 × 11/5 = 231/5 = 46 | 21/5 – 11/5 = 10/5 = 2 | 21/5 × 5/11 = 21/11 |
| 3 1/6, 1 1/6 | 18/6 + 7/6 = 25/6= 4 | 18/6 × 7/6 = 126/6 = 21 | 18/6 – 7/6 = 11/6 | 18/6 × 6/7 = 18/7 |
| 7 1/3, 1 1/3 | 22/3 + 4/3 = 26/3 | 22/3 × 4/3 = 84/3 = 28 | 22/3 – 4/3 = 17/3 | 22/3 × 3/4 = 22/4 |
Example 2: When Denominators Are Not the Same
Before any arithmetic operation, we will change the mixed fraction into an improper fraction. After that, we will find the LCM of the denominators, and then the equation is solved.
Note that since the LCM = 6, both the fractions’ denominators are multiplied by a number such that their respective denominators become equal to the LCM. To balance out this operation, the numerator of each fraction is also multiplied by the same number.
In this case, 4/3 is multiplied by 2 to become 8/6, and 3/2 is multiplied by 3 to become 9/6. Now that the denominators are the same, we can perform addition and subtraction on the two easily.

Figure 3 – When denominators of terms are not the same.
All images/mathematical drawings were created with GeoGebra.