Quadrantal Angles – Explanation and Examples

Quadrantal angles are angles whose terminal ray lies along one of the two axes in a unit circle.

Therefore, all quadrantal angles are whole number multiples of a right angle.

Quadrantal angles play an important role in trigonometry, and applications extend to physical sciences and engineering.

What Is a Quadrantal Angle?

A quadrantal angle is an angle whose measure is a whole number multiple of the measure of a right angle. These angles have a terminal ray that extends along the x or y axis in the unit circle.

In degrees, all quadrantal angles have a measure of:

$90n$, where $n$ is an integer.

In radians, all quadrantal angles have a measure of:

$\frac{\pi}{2}n$, where $n$ is again an integer.

Although there are infinitely many quadrantal angles, the ones of special interest to trigonometry are the four “standard” quadrantal angles on the unit circle. These are $0$, $90$, $180$, and $270$ degrees or $0$, $\frac{\pi}{2}$, $\pi$, and $\frac{3\pi}{2}$ radians.

All other quadrantal angles are coterminal with these angles. This means that finding the six trigonometric ratios for these four angles is enough information to know the six trigonometric ratios for all quadrantal angles.

Quadrants

Quadrantal angles separate the Cartesian plane into four quadrants. The first quadrant can be found to the upper right. This contains all of the angles between $0$ and $90$ degrees or between $0$ and $\frac{\pi}{2}$ radians.

The second quadrant is to the upper left. It contains all angles between $90$ and $180$ degrees or between $\frac{\pi}{2}$ and $\pi$ radians. The third quadrant contains angles between $180$ degrees and $270$ degrees or $\pi$ and $\frac{3\pi}{2}$ radians. 

Finally, the fourth quadrant is all of the angles between $270$ and $360$ degrees or $\frac{3\pi}{2}$ and $2\pi$ radians.

Examples of Quadrantal Angles

Examples of quadrantal angles in degrees include:

• 0 degrees
• 90 degrees
• 360 degrees
• -270 degrees

In radians, examples include:

• 0 radians
• $\frac{\pi}{2}$ radians
• $2\pi$ radians
• $-\frac{3\pi}{2}$ radians.

Examples

This section goes over common examples of problems involving quadrantal angles and their step-by-step solutions.

Example 1

Identify whether the following angles are quadrantal or not.

1. $450$ degrees
2. $9\pi$ radians
3. $-1750$ degrees

Solution

A and B are quadrantal angles, but C is not.

To determine whether or not A is quadrantal, see if there is an integer $n$ such that $90n =  450$. Solving for $n$ yields $n = 5$. Since $5$ is an integer, an angle measure $450$ degrees is quadrantal.

Similarly, there is an integer $n$ such that $\frac{\pi}{2}n = 9\pi$. Solving yields $n = 18$, which is indeed an integer.

But there is no such integer for C. Solving for $n$ in the equation $90n = -1750$ yields $-\frac{175}{9}$, which is not an integer. Therefore, it is not a quadrantal angle.

Example 2

Find the sine of all four main quadrantal angles.

Solution

Imagine a right triangle. Now imagine that an angle is getting smaller and smaller. This means that the hypotenuse of the triangle is collapsing onto the adjacent angle and the opposite side is getting smaller and smaller.

In fact, if the angle became zero, the opposite side would have no length. Since sine is equal to opposite over hypotenuse, its value would be zero as well.

On the other hand, if the angle were to get bigger and bigger, the length of the opposite side would get larger and larger along with the hypotenuse. The two would get closer and closer to the same length. Therefore, the limit of the sine as the angle goes to a right angle is $1$.

It is harder to imagine what happens as sine increases beyond a right angle without a unit circle.

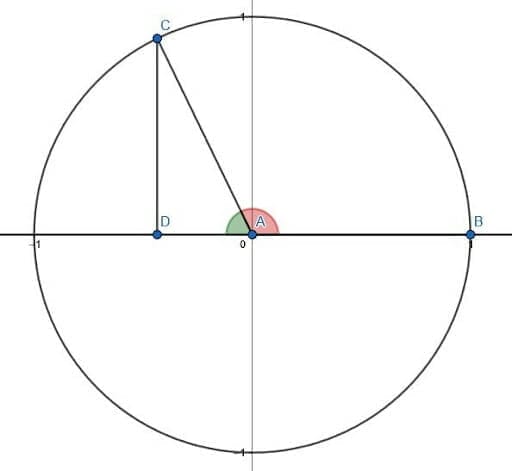
The sine of the red angle will be the same as the sine of the green angle. This is almost the same as the reflected version of the triangle that has moved over the y-axis. Therefore, as the terminal side $AC$ moves toward the x-axis and $C$ converges to the point (-1, 0), the height goes to $0$. Thus, the sine of $180$ degrees or $\pi$ radians is $0$.

Similarly, as the terminal angle moves to $270$, the length of the hypotenuse and the opposite side will again converge. This time, however, the opposite length is negative, so the limit of sine as the angle goes to $270$ degrees or $\frac{3\pi}{2}$ is $-1$.

Example 3

Name two quadrantal angles that are coterminal with a right angle.

Solution

These angles will take the form $90+360n$ or $\frac{\pi}{2}+2n\pi$, where $n$ is an integer.

There are infinitely many angles that work, but $90+360 = 450$ and $90-360 = -270$ degrees are two. In radians, those angles are $\frac{5\pi}{2}$ and $\frac{-3\pi}{2}$.

Example 4

Identify the quadrant of the angle $191$ degrees.

Solution

This angle lies in the third quadrant because it is greater than $180$ degrees and less than $270$ degrees.

Note that these types of problems are generally pretty straightforward when the given angle is between $0$ and $360$ degrees or $0$ and $2\pi$ radians. But, as the next example shows, they can be a bit trickier for larger angles or negative angles.

Example 5

Identify the quadrant of the angle $\frac{18\pi}{7}$ radians.

Solution

$\frac{18\pi}{7}$ is greater than $2\pi$ since this is equal to $\frac{14\pi}{2}$.

Therefore, to find the quadrant, it is necessary to find the standard angle equivalent to $\frac{18\pi}{7}$.

This is equal to $\frac{18\pi}{7}-\frac{14\pi}{7} = \frac{4\pi}{7}$.

Is this angle greater than or less than a right angle, $\frac{\pi}{2}$? 

Since half of $7$ is $3.5$ and $4>3.5$, $\frac{4\pi}{7}$ is greater than a right angle. But, since $4<7$, it is smaller than a straight angle, $\pi$ radians. Therefore, the angle lies in the second quadrant.