JUMP TO TOPIC
Right Angle – Explanation and Examples
A right angle is one-half of a straight line or one-fourth of a circle.
A right-angle is equal to ninety degrees or $\frac{\pi}{2}$ radians.
Right angles are ubiquitous in geometry, trigonometry, and even calculus. They are also an important input for many functions.
Before moving on with this section make sure to review types of angles and angle properties.
This section covers:
- What is a Right Angle?
- Right Angle Definition
- 90 Degree Angle Definition
What is a Right Angle?
A right angle is half of a straight line. It is the angle formed when a vertical line and a horizontal line meet or when such an angle rotates through space.
Euclid defines a right angle as:
“When a straight line standing on a straight line makes the adjacent angles equal to one another, each of the equal angles is right.”
That is, Euclid defines a right angle as one that makes two angles equal. Essentially, he defines it as half of a straight line.
In degrees, a right angle measures $90$ degrees. In radians, a right angle is $\frac{\pi}{2}$ radians.
While these measurements are often used as the basis of the definition of a right angle, using them is not the best definition since units of measurement change over time.
Right Angle Definition
A right angle is an angle equal to half of a straight line. That is, it is two rays meeting at a vertex which, if doubled, would produce a straight line.
Such an angle has a measure of $90$ degrees or $\frac{\pi}{2}$ radians.
90 Degree Angle Definition
A ninety degree angle is a right angle. It is equal to one-fourth of the interior angle a circle or half of a straight line. Consequently, a $90$ degree arc angle is equal to one-fourth of a circle.
In radians, $90$ degrees is equal to $\frac{\pi}{2}$ radians.
Note that a degree is $\frac{1}{360}$ of a circle. This number was chosen because it is divisible by all of the numbers from one to ten except seven. In addition, it is divisible by $12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120,’$ and $180.$ While most modern mathematical systems use $10$ and $2$ (and occasionally $12$), ancient systems such as those of the Sumerians and Babylonians used $60$ and $360$.
Common Examples
This section covers common examples of problems involving right angles and their step-by-step solutions.
Example 1
Find the measure of three right angles.
Solution
The measure of three right angles is equal to the measure of one right angle times three.
Since a right angle has a measure of $90$ degrees, three right angles has a measure of $90 \times 3 = 270$ degrees.
Similarly, since a right angle has a measure of $\frac{\pi}{2}$ radians, three right angles have a measure of $\frac{\pi}{2} \times 3 = \frac{3\pi}{2}$ radians.
What does three right angles looks like? Think of the angle measured counterclockwise between the minute hand and the hour hand of a clock when it is three o’clock.

This measurements makes sense because three right angles is one and a half straight lines. $1.5 \times 180 = 270$ degrees and $1.5 \times \pi = \frac{3\pi}{2}$.
Such an angle is also equal to a circle with a right angle cut out. Again, this makes sense because $360-90 = 270$ and $2\pi-\frac{\pi}{2} = \frac{3\pi}{2}$.
Example 2
Using only a ruler and a compass, construct a right angle.
Solution
There are multiple ways to do this, but this solution will use the method Euclid described in his eleventh proposition in his first book.
Begin with a straight line, $AB$.
Then, construct two circles. The first should have its center at $A$ while the second should have its center at $B$. Both should have a radius equal to the length of the line. Call one of the intersections of the circles $C$ and call the other $D$.
Finally, draw a line from $AB$ to $CD$. These two lines will meet at a right angle.
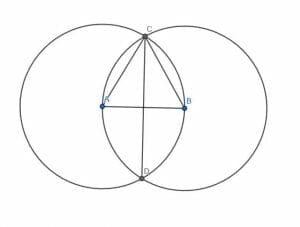
To prove this, begin by drawing lines connecting $A$ and $B$ to $C$.
Call the point where the line $CD$ intersects $AB$ $E$. The proof depends on what knowledge is assumed.
Euclid proves that the triangles $BCE$ and $ACE$ are congruent. This means that the angles $CEB$ and $CEA$ are equal. Since he defined a right angle as one formed when a line standing on another line makes the two adjacent angles equal, he says this is a right angle. That makes sense since $CE$ is standing on $AB$ and $CEB$ and $CEA$, the adjacent angles, are equal.
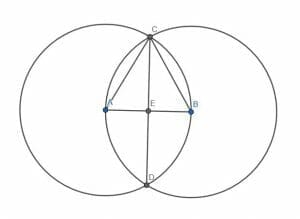
Alternatively, since $ABC$ is an equilateral triangle ($AB$, $BC$, and $AC$ are all radii of circles with equivalent radii), the angle $EBC$ is $60$ degrees and $BCE$ is half of that, $30$ degrees.
If it is assumed that a triangle has $180$ degrees, then the remaining angle $CEB$ must be $180-(60+30) = 90$ degrees, or a right angle.
Example 3
Is the angle $ACB$ below right? Why or why not?
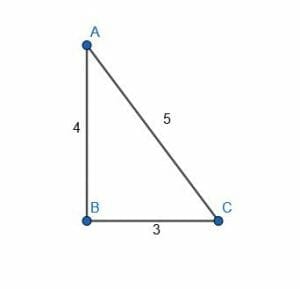
Solution
The angle $ACB$ is a right angle because it is the largest angle in a right triangle.
The key to this problem lies in knowing that the triangle is right. There are two facts that, when combined, indicate this.
- SSS congruency
- The Pythagorean Theorem
SSS congruency is side-side-side congruency. This means that if two triangles have all of the same side measures, their corresponding angles are also the same. That is, there is only one way to construct a triangle with three given lengths (and then only if the lengths satisfy the triangle inequality, which states each length must be less than the sum of the other two).
The second fact, the Pythagorean Theorem, states that, in a right triangle, the sum of the squares of the two sides forming the right angle is equal to the square of the third side. Famously, this is written as $a^2+b^2=c^2$.
In the given triangle, the sides have lengths of $3$, $4$, and $5$ units. These three values satisfy the Pythagorean Theorem because $3^2+4^2 = 9+16 = 25 = 5^2$. Therefore, there exists a right triangle where the legs of length $3$ and $4$ units have a third side of $5$ units.
But, SSS congruency asserts that if there is only one triangle with side lengths of $3, 4$, and $5$ units. Therefore, this triangle must also be a right triangle and the angle formed when the legs of length $3$ and $4$ meet is the right angle.
But this is the angle $ACB$. Therefore, the angle $ACB$ is indeed a right angle.
Example 4
Let $AC$ be a diameter of the circle with center $C$ and radius $CB$ and let $D$ be any point on the circumference of the circle. Show that triangle $CDB$ inside the circle is a right triangle with $CDB$ as a right angle.
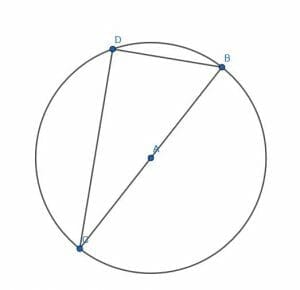
Solution
Part 1
The proof requires a little bit of construction.
First, draw a straight line connecting $D$ and $A$. Then, extend this line to a point E on the other side of the circle.
Next, connect the points $B$ and $C$ to $E$.
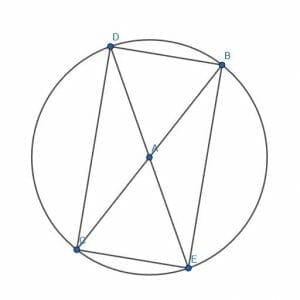
Note first that the line $DE$ is a diameter because any line connecting two points on a circle’s circumference and passing through the center is a diameter.
Therefore, the segments $AB$, $AC$, $AD$, and $AE$ all are radii of the circle and consequently have the same length.
Next, note that the angles $DAB$ and $CAE$ are equal because they are vertical angles. Similarly, $CAD$ and $EAB$ are equal.
Part 2
Then, by SAS (side-angle-side) congruency, the triangles $DAB$ and $CAE$ are congruent as are the triangles $CAD$ and $EAB$. This means that the corresponding bases are equal. Specifically, $DB$ and $CE$ are equal as are $DC$ and $BC$.
In addition, because the radii are all equal, each of the triangles $DAB$, $CAE$, $CAD$, and $EAB$ are isosceles triangles. This means that their base angles will be equal to each other. Specifically, the angles $ADB$, $DBA$, $ACE$, and $CEA$ are all equal as are $ABE$, $BEA$, $ADC$, and $DCA$.
Since $DB = CE$ and $DC = BC$, the quadrilateral $DBEC$ is a parallelogram. Thus, opposite angles $DBE$ and $ECD$ are equal as are the opposite angles $BEC$ and $CDB$.
Note, however, that the angle $DBE$ is equal to the angle $CDB$. The first is made up of two smaller angles, $DBA$ and $ABE$. The second is also made up of two smaller angles $CDA$ and $ADB$.
In these, however, $CDA$ and $ABE$ are equal because they are corresponding angles in congruent triangles. Likewise, $ADB$ and $DBA$ are equal in measure because they are base angles in an isosceles triangles.
Therefore, the angles $DBE$ and $CDB$ must also have the same measure. But, since this is a parallelogram, $BEA = CDB = DBE = ECD$. Thus, all of the angles are the same.
If all of the angles in a quadrilateral have the same measure, then all of the angles must be equal to $\frac{360}{4} = 90$ degrees. This is because a quadrilateral has $360$ degrees of interior angles.
Thus, since each angle, and in particular the angle $DBE$, has a measure of $90$ degrees, each angle is a right angle.
Example 5
Use a right triangle to find the sine of a right angle.
Solution
Recall that sine is a function with angles as an input and ratios as an output.
Specifically, sines are the ratio of an angle’s opposite angle divided by the hypotenuse in a right triangle.
If the angle in question is the right angle, then the hypotenuse and the opposite side are one and the same. Therefore, the ratio is $1$.
More Examples with Explanation
- Calculate the measure of five right angles.
- Find the cosine of a ninety degree angles. (Hint: In this case, it helps to consider the limit as one of the smaller angles in a right triangle goes to 90 degrees.)
- A triangle has sides measuring $7, 8,$ and $9$ units. Is it a right triangle? Why or why not?
- Using only a ruler and a compass, construct a line that passes through the given point and meets the given line at a right angle.
- How long does it take the Earth to rotate ninety degrees?
Answer Key
- $450$ degrees.
- $0$. This is because as one angle goes to $90$ degrees, the other goes to $0$. Therefore, the length of the adjacent side decreases to $0$ as the hypotenuse collapses onto the opposite side.
- No, because the side measures do not satisfy the Pythagorean Theorem.
- Since the Earth rotates approximately $360$ degrees in $24$ hours, it takes the Earth approximately $6$ hours to rotate $90$ degrees.
