JUMP TO TOPIC
Rotation in Geometry — Examples and Explanation
 A rotation in geometry moves a given object around a given point at a given angle.
A rotation in geometry moves a given object around a given point at a given angle.
The given point can be anywhere in the plane, even on the given object. The angle of rotation will always be specified as clockwise or counterclockwise.
Before continuing, make sure to review geometric transformations and coordinate geometry.
This section covers:
- What is a Rotation in Geometry?
- How to Do Rotations in Geometry
- Geometric Rotation Definition
What is a Rotation in Geometry?
A rotation in geometry is a transformation that has one fixed point. The geometric object or function then rotates around this given point by a given angle measure. This measure can be given in degrees or radians, and the direction — clockwise or counterclockwise — is specified.
The most common point of rotation is the origin (0, 0). The point of rotation may be a vertex of a given object or its center in other situations.
How to Do Rotations in Geometry
As with other transformations, begin by finding the key points’ coordinates in the given function or object.
Then, draw a line segment from each of the key points to the point of rotation.
Next, for each of these line segments, create a new segment of equal length such that one endpoint of the new segment is the point of rotation. Then, orient the copied segment to form the given angle in the given direction with the original line segment.
The location of the endpoint of this new segment is the rotation of the key point that is the endpoint of the original line segment.
Geometric Rotation Definition
A geometric rotation is a transformation that rotates an object or function about a given, fixed point in the plane at a given angle in a given direction.
Examples
This section covers common examples of problems involving geometric rotations and their step-by-step solutions.
Example 1
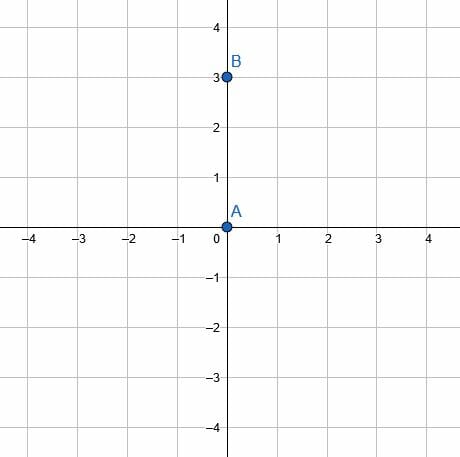
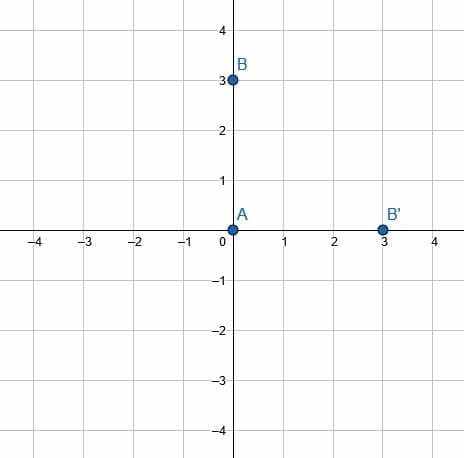
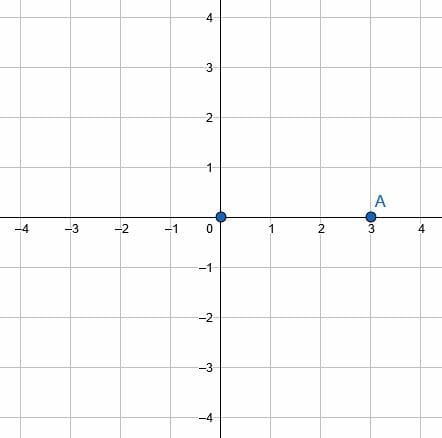
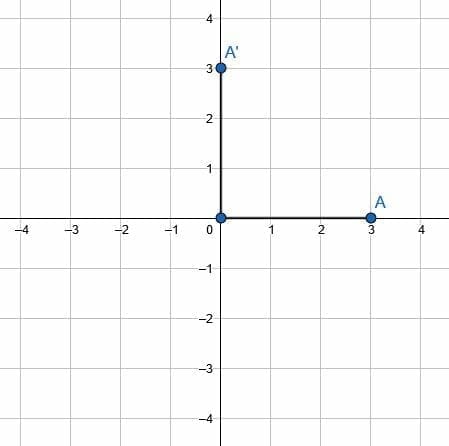
Let point A have coordinates (3, 0). Rotate point A about the origin by 90 degrees counterclockwise.
Example 1 Solution
First, plot the point on the coordinate plane.
Then, create a line segment connecting A to the origin.
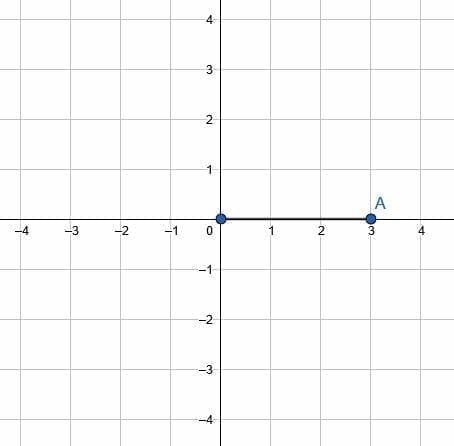
Note that the length of this segment is 3 units. Next, create a second line segment of the same length, 3 units, with one endpoint at the origin. Call the other end of this segment A’.
Finally, orient the line segment with endpoint A’ so that this segment and the original segment form a 90-degree angle counterclockwise. This puts A’ at the point (0, 3), which is the required rotation.
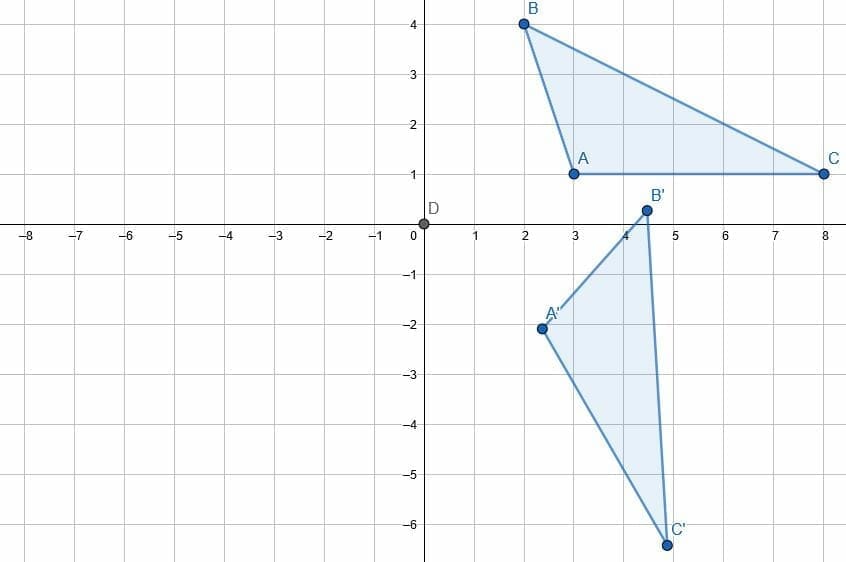
Example 2
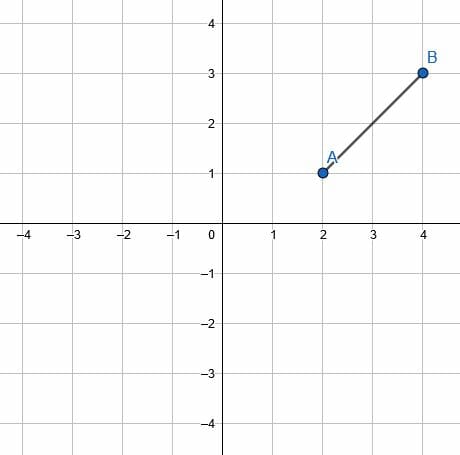
Rotate the given line segment about the origin by 60 degrees clockwise.
Example 2 Solution
Note that the two key points, A and B, have coordinates (2, 1) and (4, 3). The first step is then to connect these points to the point of rotation, the origin.
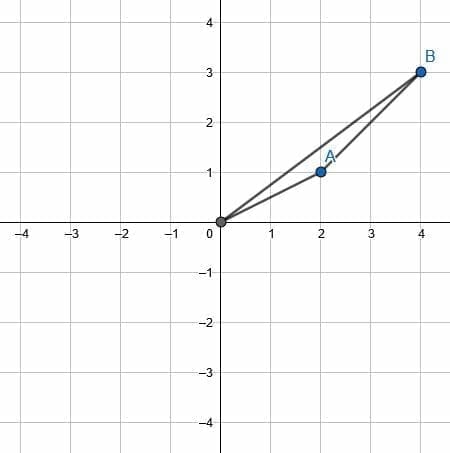
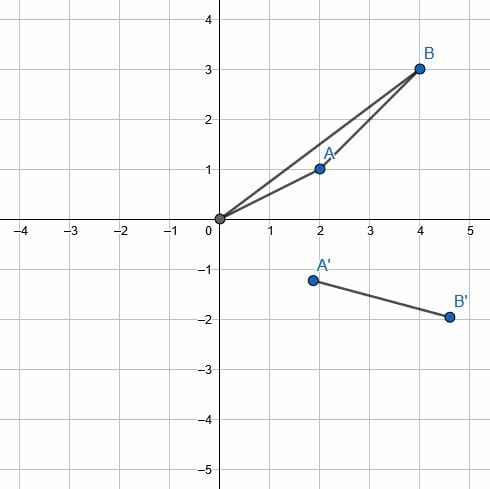
Now, create copies of each of these lines with endpoints A’ and B.’ The two line segments need to be oriented so that OB and OB’s segments form a 60-degree clockwise angle and OA and OA’ similarly form a 60-degree clockwise angle.
Then, connect the points A’ and B’ to finish the transformation.
Example 3
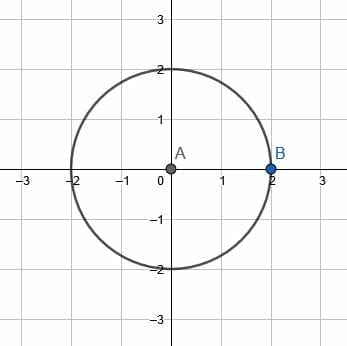
Rotate the given circle about its center by 45 degrees counterclockwise.
Example 3 Solution
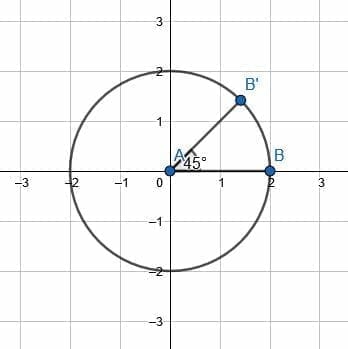
Notice that the shape of the circle does not change when it rotates around its center. That is the points on the circle map to other points on the circle.
In this case, however, there is a given point on the circle, B. To find B’, that is, the location of B after completing the given rotation, we first construct the line AB.
This is the radius of the circle. Then, create a counterclockwise angle of 45 degrees with another radius of the circle. The endpoint of this second line segment is B’.
Example 4
Rotate the triangle ABC 180 degrees around vertex A.
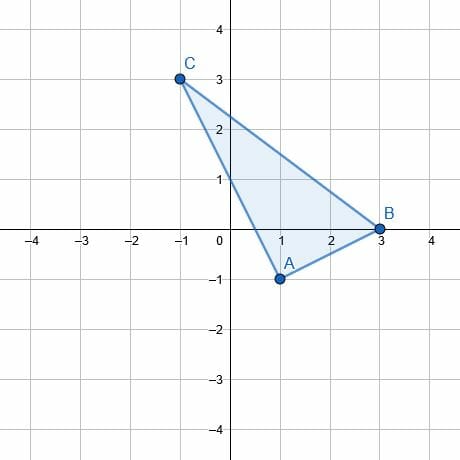
Example 4 Solution
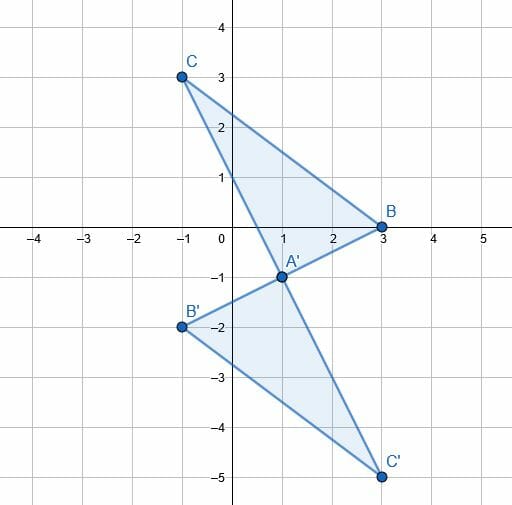
Because the given angle is 180 degrees, the direction is not specified. A point that rotates 180 degrees counterclockwise will map to the same point if it rotates 180 degrees clockwise.
In this case, since A is the point of rotation, the mapped point A’ is equal to A.
To find B, extend the line AB through A to B’ so that AB’ is equal to AB. Likewise, to find C, extend AC through A to a point C’ so that AC’ is equal to AB.
Finally, connect the vertices A’, B’, and C’. The resulting figure is the transformed triangle.
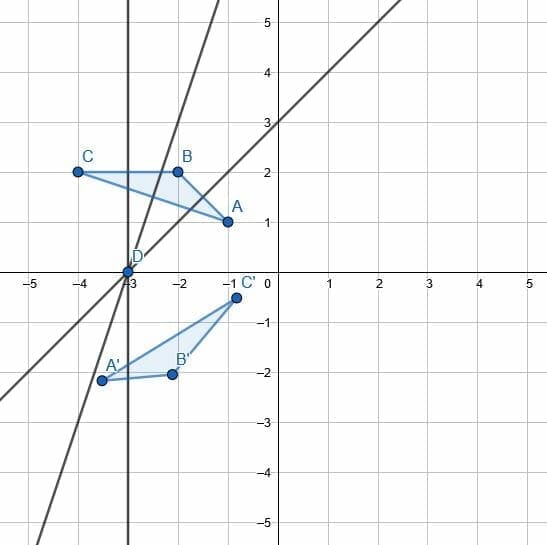
Example 5
Find the fixed point of rotation.
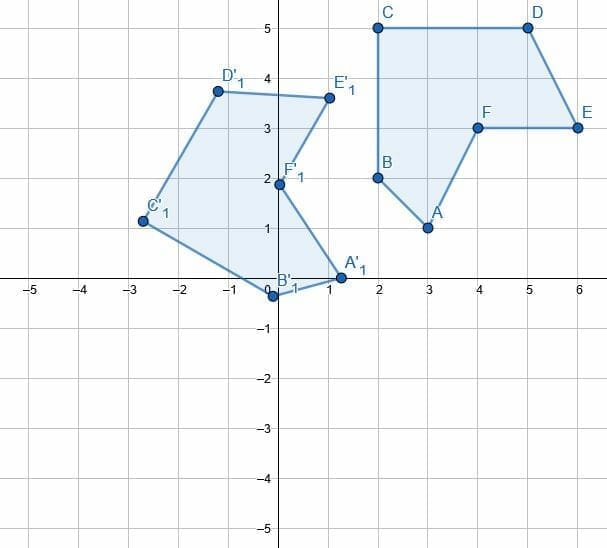
Example 5 Solution
In this case, we are not given an angle of rotation, nor are we asked to find it. It may seem at first like there is not enough information to answer the question.
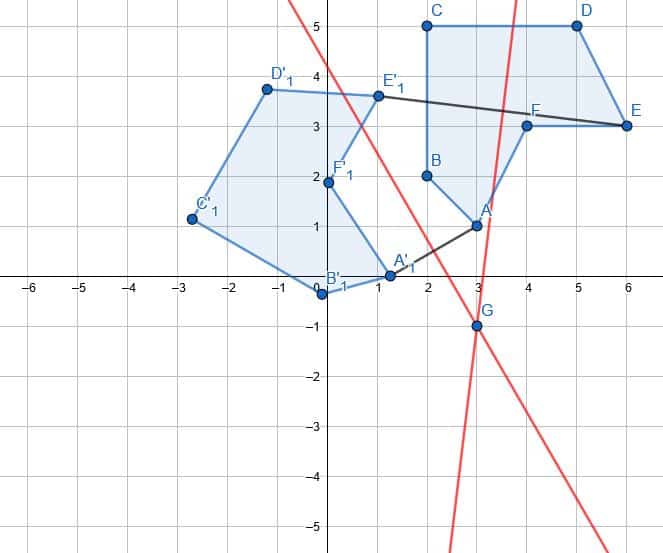
Remember that a line drawn from any point on the original figure to the point of rotation and a line drawn from the corresponding point on the transformed figure will have the same length. This means that a figure that includes those two segments and a third line connecting the original point and its corresponding point is an isosceles triangle.
Therefore, a perpendicular bisector for the line connecting a point and its transformation will pass through the point of rotation. This is because this base is the base of the isosceles triangle described above, and a perpendicular bisector of the base of an isosceles triangle passes through the vertex.
But, there are infinitely many points along this line. The point of rotation could be any of them. Therefore, we have to construct two such perpendicular bisectors, say for AA’ and EE’. The intersection of these bisectors is the point of rotation, G.
Practice Questions
![]()
Open Problems
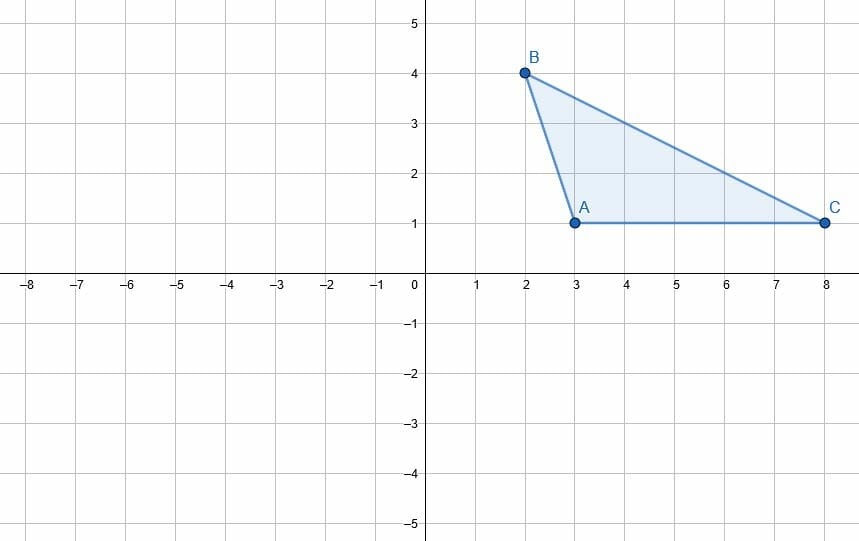
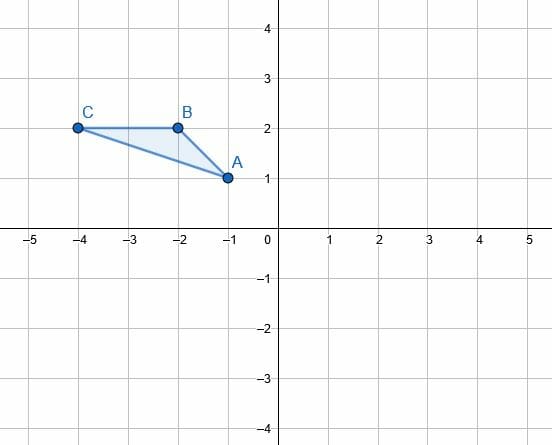
- Rotate point B 270 degrees counterclockwise about the origin.

- Rotate the triangle ABC 60 degrees clockwise about the origin.

- Rotate the triangle $130$ degrees clockwise about the circumcenter.

Open Problem Solutions
Images/mathematical drawings are created with GeoGebra.