JUMP TO TOPIC
Sum and Difference Formulas – Explanation and Examples
In trigonometry, sum and difference formulas are equations involving sine and cosine that reveal the sine or cosine of the sum or difference of two angles.Sum and difference formulas require both the sine and cosine values of both angles to be known. They make it easy to find minor angles after memorizing the values of major angles.Like other trig identities, the sum and difference formulas are useful in engineering and physical sciences. Make sure to review trigonometric identities before reading more about the sum and difference formulas.Sum Formula
The sum formula is an identity that shows the relationship between sine and cosine values for two angles and the sum of a trigonometric function for those two angles.That is, for a given trigonometric function $fun$, the sum formula gives a value for $funx+funy$ for any two angles $x$ and $y$ radians.There are sum formulas for both sine and cosine. Since the other four trigonometric functions can be derived from these two functions, equations for their sum and difference also exist.Note, however, that the sine and cosine sum formulas both require that the sine and cosine of both angles be known. That is, the sum formula for $sinx+siny$ requires that $sinx, siny, cosx,$ and $cosy$ are known. Similarly, the sum formula for $cosx+cosy$ requires that $sinx, siny, cosx,$ and 4cosy$ are known.Origin of Sum and Difference Formulas
The great twelfth-century Indian mathematician Bhaskara II made important contributions to the mathematics of trigonometry. Like many early mathematicians, Bhaskara II became interested in studying trigonometry because of his studies in astronomy, but he was one of the first to be interested in the subject itself beyond its utility.Because of this, he made a table of sine values. He also discovered the formula for both the sine of the sum of two angles and the sine of the difference of two angles.The mathematician Claudius Ptolemy of second-century Alexandria also had a formula for a precursor to the sine and cosine angle sum formulas. In his time, trigonometry focused on chords instead of the ratio between sides of right triangles.Ptolemy made a table of chord values (similar to a table of sine values) to help him with his astronomy work. Although he did not use sine and cosine, his chord function can be converted to the modern trig function sine. In particular, $chord(x) = 120sin(\frac{x}{2}).After accounting for the conversion of the function, Ptolemy’s chord angle sum and difference identities are the same as the modern sine and cosine angle sum and difference identities.Sum Formula for Sine
The sum formula for sine is:$sin(x+y) = sinxcosy+cosxsiny$.That is, the sine of the sum of any two angles $x$ and $y$ is the sum of the sine of $x$ times cosine of $y$ and the cosine of $y$ times the sine of $x$.This is also where the equation $sin(2x)=2sinxcosx$ comes from. Since $sin(2x) = sin(x+x)$, $sin(2x) = sinxcosx+cosxsinx = 2sinxcosx$.Proof of Sum Formula for Sine
Although there are many proofs for the sine angle sum formula, most are relatively complicated. The one shown here needs an accompanying figure.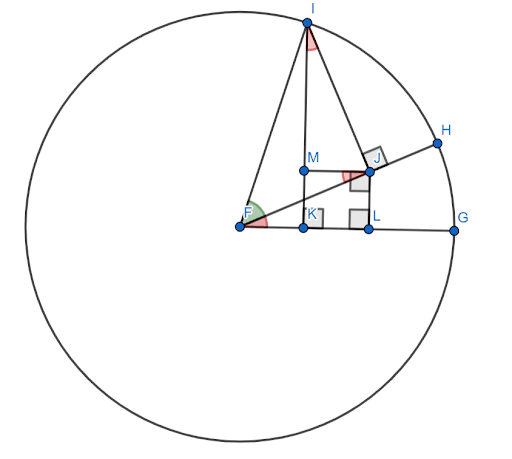
Assume this figure is constructed on the unit circle with $FG$ as the x-axis. Let the red angle (HFG) be the angle $x$ and let the green angle (HFI) be the angle $y$. Then, the angle $x+y$ is the angle $GFI$.It is required to show that the sine of this angle is equal to $sinxcosy+cosxcosy$.Now the angles $FJM$ and $JIM$ are equal to the angle $x$ because of similar triangles since $FI=1$, $siny=IJ$ and $cosy=FJ$.Then, by definition of sine, $sinx = \frac{JL}{FJ}$. Therefore, $FJsinx=JL$. But, $FJ=cosy$, so $JL = cosysinx$.Similarly, $cosx = \frac{IM}{IJ}$. Therefore, $IJcosx=IM$. But, $IJ=siny$, so $sinycosx = IM$.Now, by construction, $JLKM$ is a square. Therefore, $JL=MK$.Then, by the construction of the unit circle, the sine of the angle $x+y$ is the segment $IK$. This can be broken up into two smaller segments, $IM$ and $MK$.It has already been shown that $IM = sinycosx$. But, since $MK = JL$ and $JL = cosysinx$, $MK = cosysinx$.Therefore, $sin(x+y) = IK = IM+MK = sinycosx+cosysinx$.The other sum and difference formulas for sine and cosine follow similarly.Sum Formula for Cosine
The sum formula for cosine is:$cos(x+y) = cosxcosy-sinxsiny$.That is, the cosine of the sum of any two angles $x$ and $y$ is the sum of the cosine of $x$ times the cosine of $y$ and the sine of $x$ times the sine of $y$.This is also where the equation $cos(2x) = cos^2x-sin^2x$ comes from. Since $cos(2x) = cos(x+x)$, $cos(2x) = cosxcosx-sinxsinx = cos^2x-sin^2x$.Tangent Sum Formula
Since both sine and cosine have a formula for the sum of two angles, there is also a formula for the tangent of the sum of two angles.Just using the sine and cosine formulas, the tangent of $x+y$ for any two angles $x$ and $y$ is:$tan(x+y) = \frac{sin(x+y)}{cos(x+y)} = \frac{sinxcosy+cosxsiny}{cosxcosy-sinxsiny}$.Alternatively, the tangent of the sum of two angles is:$tan(x+y) = \frac{tanx+tany}{1-tanxtany}$.To see this, begin with the expanded form $tan(x+y) = \frac{sinxcosy+cosxsiny}{cosxcosy-sinxsiny}$. Then, divide both the numerator and denominator by $cosxcosy$. This yields:$tan(x+y) = \frac{sinxcosy+cosxsiny}{cosxcosy-sinxsiny} = \frac{\frac{sinxcosy}{cosxcoxy}+\frac{cosxsiny}{cosxcosy}}{\frac{cosxcosy}{cosxcosy}+\frac{sinxsiny}{cosxcosy}}$.Then, this simplifies to $\frac{tanx+tany}{1-tanxtany}$.Difference Formula
The difference formula gives the trigonometric ratio for the difference between two angles if the sine and cosine of the original two angles are known. Like the sum formula, it provides a way to find trigonometric ratios for minor angles if major angles are known.There is a difference formula for both sine and cosine. Both formulas use both sine and cosine ratios for both of the initial angles.Again, recall that the other four trigonometric ratios follow from sine and cosine. Thus, the tangent, cotangent, cosecant, and secant of the difference of two angles can be found using the sine and cosine difference formulas.Difference Formula for Sine
The difference formula for sine is the formula for the sine of an angle that is equal to the difference of two angles, $x$ and $y$. This formula depends on the sine and cosine of both $x$ and $y$.$sin(x-y)=sinxcosy-cosxsiny$.Recall that the sine function is odd. This means that for any angle $x$, $sin(-x) = -sinx$.This means that the order of the angle is important for the difference formula. That is, $sin(x-y) \neq sin(y-x)$. In fact, since $y-x = -(x-y)$, $sin(y-x) = sin(-(x-y) = -(sinxcosy-cosxsiny) = cosxsiny-sinxcosy$.Difference Formula for Cosine
The difference formula for cosine is the formula for the cosine of an angle that is equal to the difference of two angles, $x$ and $y$. Like the difference formula for sine, this formula depends on both the sine and cosine of both $x$ and $y$.$cos(x-y) = cosxcosy+sinxsiny$.Take note that the order of $x$ and $y$ does not matter in this formula. That is, since $cos(y-x) = cosycosx+sinysinx = cosxcosy+sinxsiny = cos(x-y)$.This makes sense because cosine is an even function. Recall that even functions have the same y-value for positive and negative x-values. That is, $cos(-x) = cosx$. Then, since $y-x = -(x-y)$, $cos(y-x) = cos(x-y)$.Tangent Difference Formula
The tangent difference formula can be derived from the difference formulas for sine and cosine. For two angles $x$ and $y$, the tangent of the difference of $x$ and $y$ is:$tan(x-y) = \frac{tanx-tany}{1+tanxtany}$.Since tangent is equal to the sine divided by the cosine, the tangent of the difference of two angles $x$ and $y$ is:$tan(x-y) = \frac{sin(x-y)}{cos(x-y)}$.Using the difference formulas for sine and cosine, this is:$tan(x-y) = \frac{sinxcosy-cosxsiny}{cosxcosy+sinxsiny}$.Similar to the sum formula for the tangent, derive the tangent difference formula by dividing both the numerator and denominator by $cosxcosy$.$tan(x-y) = \frac{\frac{sinxcosy-cosxsiny}{cosxcosy}}{\frac{cosxcosy+sinxsiny}{cosxcosy}}$.This simplifies to:$tan(x-y) = \frac{tanx-tany}{1+tanxtany}$.Like the sine function, the tangent function is odd. Therefore, $tan(y-x) = tan(-(x-y)) = -tan(x-y) = -(\frac{tanx-tany}{1+tanxtany}) = \frac{tany-tanx}{-1-tanxtany}$.Other Sum and Difference Formulas
The proofs for the sum and difference formulas for the other trigonometric functions, namely cotangent, cosecant, and secant, can be derived from the angle sum and difference formulas for sine and cosine.While it is preferable for sine and cosine formulas to be in terms of sine and cosine, this is not true for other trigonometric functions. In general, cosecant and secant formulas should be in terms of cosecant and secant. For cotangent formulas, they should be in terms of cotangent (just as tangent formulas should be in terms of tangent).Generally, deriving these formulas involves first using the definitions of the reciprocal functions. Then, divide the numerator and denominator of the resulting expression by the same term to force it into terms of secant and cosecant or terms of cotangent.An example of this for the general formulas for the angle sum and angle difference of cosecant is in example 4. Then, practice problem 3 involves deriving the formulas for the angle sum and angle difference of secant.For cotangent, the formula for angle sum is:$cot(x+y) = \frac{cotxcoty-1}{cotx+coty}$.Then, the formula for the angle difference is:$cot(x-y) = \frac{cotxcoty+1}{cotx-coty}$.Undefined Values
For secant, cosecant, tangent, and cotangent, some values are undefined. This is because these functions can be written to have other trig functions in the denominator.Specifically, $secx = \frac{1}{cosx}$, $cscx = \frac{1}{sinx}$, $tanx = \frac{sinx}{cosx}$, and $cotx = \frac{sinx}{cosx}$.Since both sines of an angle and cosines of an angle can be $0$, these functions all have angles for which they are undefined.Consequently, it is impossible to use the sum and difference formulas for angles that have a sum or difference of an undefined point.For example, cotangent is not defined at $0$ because sine is equal to $0$ at $0$ radians. But the cotangent of any two angles that add up to $0$ will be undefined based on its formula. Specifically:$cot(0) = cot(x-x) = \frac{cotxcot(x)+1}{cotx-cotx}$.But the denominator here is $cotx-cotx = 0$. Therefore, $cot(0)$ is undefined, even using the difference formula.Examples
This section goes over common examples of problems involving the sum and difference formulas and their step-by-step solutions.Example 1
Write a general formula for the sine of the sum of three angles $x, y,$ and $z$ radians. Hint: use the sum formula twice.Solution
This formula will require the formula for the sine of the sum of two angles. In fact, it will be used twice.To begin, let $w=x+y$. Now, the sine of the sum of $x, y,$ and $z$ is the sum of $w$ and $z$. That is:$sin(x+y+z) = sin(w+z)$.By the angle sum formula for sine, the sine of $w+z$ is:$sin(w+z) = sinwcosz + sinzcosw$.Now, since $w=x+y$, the sine of $w$ is equal to the sine of $x+y$. That is, $sin(w) = sin(x+y)$. By the formula for the sine of a sum, this is:$sin(w) = sin(x+y) = sinxcosy + sinycosx$.Note that $sin(w+z)$ also depends on the cosine of $w$. Using the formula for cosine of a sum, this is:$cos(w) = cos(x+y) = cosxcosy + sinxsiny$.Now, plug the equations for $sin(w)$ and $cos(w)$ back into the original equation for $sin(w+z)$.$sin(w+z) = sinwcosz+sinzcosw = (sinxcosy+sinycosx)cosz + sinz(cosxcosy+sinxsiny)$.Then, distribute to get:$sinxcosycosz + sinycosxcosz+sinzcosxcosy + sinxsinysinz$.None of these are like terms, so this is the formula for the sum of three angles. Since this is a rather long formula, it is usually not included in general formulas for trig identities.$sin(x+y+z) = sinxcosycosz+sinycosxcosz+sinzcosxcosy+sinxsinysinz$.Example 2
Find the sine of the angle $\frac{7\pi}{12}$ radians. Use the sum formula and the fact that $\frac{7\pi}{12} = \frac{3\pi+4\pi}{12} = \frac{\pi}{4}+\frac{\pi}{3}$ radians to help.Solution
By the angle sum formula for sine, the sine of the sum of two angles is equal to:$sinxcosy+sinycosx$.In this case, $\frac{7\pi}{12} = \frac{\pi}{4}+\frac{\pi}{3}$. Therefore, let $\frac{\pi}{4}$ be $x$, and let $\frac{\pi}{3}$ be $y$. Therefore:$sin(\frac{\pi}{12}) = sin(\frac{\pi}{4})cos(\frac{\pi}{3}) + sin(\frac{\pi}{3})cos(\frac{\pi}{4})$.Since $\frac{\pi}{4}$ and $\frac{\pi}{3}$ are major angles, their sine and cosine values are either memorized or easily accessible in a table. Specifically:- $sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}$
- $cos(\frac{\pi}{3}) = \frac{1}{2}$
- $sin(\frac{\pi}{3}) = \frac{\sqrt{3}}{2}$
- $cos(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}$.
Example 3
Find the cosine of $-\frac{\pi}{12}$ radians using the angle sum and difference formulas for cosine.Solution
The angle $-\frac{\pi}{12}$ radians is not a major angle. Most people only memorize the trigonometric ratios of the major angles $\frac{\pi}{6}$, $\frac{\pi}{4}$, and $\frac{\pi}{3}$ and their corresponding angles in other quadrants. Alternatively, these angles are the ones most likely to be in a table or graphic.This means that an exact value for the cosine of $-\frac{\pi}{12}$ radians must be found using these major angle values. In this case, $-\frac{\pi}{12} = \frac{\pi}{6}-\frac{\pi}{4}$, so the difference formula will yield the exact ratio.Recall that the difference formula for cosine is:$cos(x-y) = cosxcosy + sinxsiny$.In this case, let $x$ be $\frac{\pi}{6}$, and let $y$ be $\frac{\pi}{4}$. Thus, cosine of $-\frac{\pi}{12}$ is:$cos(\frac{\pi}{6})cos(\frac{\pi}{4}) + sin(\frac{\pi}{6})sin(\frac{\pi}{4})$.Both the sine and cosine of the angle $\frac{\pi}{4}$ are $\frac{\sqrt{2}}{2}$. Then, the sine of $\frac{\pi}{6}$ is $\frac{1}{2}$, and the cosine is $\frac{\sqrt{3}}{2}$.Therefore, plugging these values into the equation:$cos(-\frac{\pi}{12}) = (\frac{\sqrt{2}}{2})(\frac{\sqrt{3}}{2}) + (\frac{1}{2})(\frac{\sqrt{2}}{2})$.Then, this simplifies to:$\frac{\sqrt{2}\sqrt{3}}{4} + \frac{\sqrt{2}}{2} = \frac{\sqrt{2}(\sqrt{3}+1)}{4} = \frac{\sqrt{3}+1}{2\sqrt{2}}$.Example 4
Use the sum and difference formulas for sine and cosine to find the sum formula for cosecant. Then, use a similar process to find the difference formula for cosecant.Solution
Cosecant Sum Formula
Since the cosecant is the reciprocal of the sine, the cosecant of the sum of two angles $x$ and $y$ is:$csc(x+y) = \frac{1}{sin(x+y)}$.Then, using the formula for the sine of the sum of two angles, this is equal to:$csc(x+y) = \frac{1}{sinxcosy+sinycosx}$.While this works as a formula, formulas for cosecant and secant generally depend on only secant and cosecant. Thus, it is necessary to manipulate the right side of the equation so that it does not have sine and cosine but rather a cosecant and secant.To do this, begin by dividing both the numerator and denominator by $cosxcosysinxsiny$.This yields:$\frac{\frac{1}{cosxcosysinxsiny}}{\frac{sinxcosy+sinycosx}{cosxcosysinxsiny}}$.This then simplifies to:$\frac{secxsecycscxcscy}{secxcscy+cscxsecy}$.Since this is only in terms of secant and cosecant, this is the general formula for the cosecant of the sum of two angles.Cosecant Difference Formula
Again, since the cosecant is the reciprocal of sine, the difference formula for cosecant is:$csc(x-y) = \frac{1}{sinxcosy – sinycosx}$.As before, this equation is true, but it is preferable that formulas for cosecant use only cosecant and secant. Therefore, it is required to algebraically manipulate this equation so it only uses those to functions.Once again, begin by dividing both the numerator and denominator of the right side by the product of $sinx, cosy, siny,$ and $cosx$. This yields:$csc(x-y) = \frac{\frac{1}{sinxcosysinycosx}}{\frac{sinxcosy – sinycosx}{sinxcosysinycosx}}$.Now, this can be simplified further:$csc(x-y) = \frac{cscxsecycscysecx}{cscysecx – cscxsecy}$.This formula looks similar to the cosecant sum formula, $\frac{secxsecycscxcscy}{secxcscy + cscxsecy}$. The only difference is that the denominator is a sum instead of a difference.Example 5
Find the tangent of the angle $\frac{13\pi}{12}$ radians by first finding the tangent of $\frac{\pi}{12} = \frac{\pi}{3}-\frac{\pi}{4}$ radians and then finding the tangent of the sum of $\pi$ and $\frac{\pi}{12}$ radians.Solution
This problem requires multiple steps. Specifically, it sets up the angle $\frac{11\pi}[12}$ radians as:$\frac{13\pi}{12} = \pi+(\frac{\pi}{3}-\frac{\pi}{4})$.Begin by finding the tangent of the difference between $\frac{\pi}{3}$ and $\frac{\pi}{4}$. The formula for the tangent of the difference is:$\frac{tanx-tany}{1+tanxtany}$.The tangent of $\frac{\pi}{4}$ radians is 1 because sine and cosine are equal at that angle. At $\frac{\pi}{3}$, the sine is $\frac{\sqrt{3}}{2}$ and cosine is $\frac{1}{2}$. Therefore, the tangent is $\sqrt{3}$. Plugging these values into the expression above yields:$\frac{\sqrt{3}-1}{1+\sqrt{3}}$.This expression simplifies nicely by forcing the difference of squares in the denominator. To do this, multiply the expression by $1 = \frac{\sqrt{3}-1}{\sqrt{3}-1}$. This yields:$\frac{(\sqrt{3}-1)^2}{3-1} = \frac{3-2\sqrt{3}+1}{2} = \frac{4-2\sqrt{3}}{2} = 2-sqrt{3}$.Tangent Sum
Next, find the tangent of the sum $\pi+\frac{\pi}{12}$ radians. The sum formula for tangent is:$\frac{tanx+tany}{1-tanxtany}$.At $\pi$ radians, sine is $0$ and cosine is $1$. Therefore, the tangent at $\pi$ radians is also $0$. Plugging this value and the tangent ratio for $\frac{\pi}[12}$ found above, the tangent of $\frac{13\pi}{12}$ is:$\frac{0+2-sqrt{3}}{1-(0)(2-sqrt{3})$.This simplifies to:$\frac{2-sqrt{3}){1} = 2-\sqrt{3}$In fact, the tangents of these two angles, $\frac{13\pi}{12}$ radians and $\frac{\pi}{12}$ radians, are equal. This makes sense since the tangent is $\pi$ periodic. Any time $\pi$ is added to an angle $x$, the numerator of the tangent of the sum is $0+tanx$. Then, the denominator will be $1+0 = 1$. This will always simplify to $tanx$.Example 6
Use the values to find the sine, cosine, and tangent of $2^{\circ}$ and $38^{\circ}. All values are approximated to the nearest thousandth.$sin(18^{\circ}) = 0.309$$sin(20^{\circ}) = 0.342$$cos(18^{\circ}) = 0.951$$cos(20^{\circ}) = 0.940$Solution
This is a multiple step problem since there are, in total, six values to find. Specifically, they are:- $sin(2^{\circ}) = sin(20^{\circ}-18^{\circ})$
- $cos(2^{\circ}) = cos(20^{\circ}-18^{\circ})$
- $tan(2^{\circ}) = tan(20^{\circ}-18^{\circ})$
- $sin(38^{\circ}) = sin(20^{\circ}+18^{\circ})$
- $cos(38^{\circ}) = cos(20^{\circ}+18^{\circ})$
- $tan(38^{\circ}) = tan(20^{\circ}+18^{\circ})$
