Translation in Geometry — Examples and Explanation

A translation in geometry is any vertical or horizontal shift applied to an object.

The direction of the shift is always specified. Since only the location of the object changes and not the size, translations are rigid transformations.

Since translations involve units and finding points in the coordinate plane, it is good to review coordinate geometry before jumping into the section.

This topic will cover:

• What is a Translation in Geometry?
• How to Do Translation
• Translation in Geometry Definition

What is a Translation in Geometry?

A translation is a movement horizontally to the left or right or vertically up or down in geometry. It can also include a combination of the two.

Since translations preserve the size and shape of an object, they are rigid transformations. That is, the only thing that changes about an object when a translation is applied is its location on the coordinate plane.

How to Do Translation

The easiest way to do a transformation in geometry is to find the key points of the geometric object and translate those. Then, you can “connect the dots” to complete the object.

If, instead, you need to describe a translation, compare the coordinates of the key points of the first figure with the second. A verbal description notes the number of units shifted horizontally and vertically and the directions. There are also mathematical ways to describe translations.

There are two main ways to do this. The first is through function mapping notation. That is:

$f(x) → f(x-a)+b$

In this case, the function moves $a$ units to the right and $b$ units up. If $a$ is negative, the function moves left, and if $b$ is negative, the function moves down.

Alternatively, a translation can be denoted:

$(x, y) → (x+a, y+b)$

Here, all of the points of the function shift $a$ units right and $b$ units up.

Translation in Geometry Definition

While the word “translation” may make many people think of language, the Latin roots mean “carried across.” In language, the meaning is carried across cultures through translation.

A translation carries an object across the coordinate plane, keeping its size and shape the same in math. Its orientation and area are also constant after a translation.

Simply put, a translation in math is a vertical shift, horizontal shift, or a combination of the two.

Examples

This section covers common examples of problems involving translations in geometry and their step-by-step solutions.

Example 1

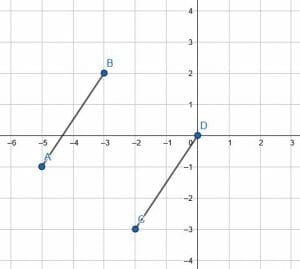
Determine the translation applied to the line segment.

Example 1 Solution

Since the prompt tells us that only a translation has occurred, we will presume that A translates to C and B translates to D. Otherwise, we must a rotation must also be included.

To find the translation, compare the positions of A and C. Moving from A to C requires moving down two units and then moving three units to the right.

Likewise, moving from B to D requires moving down two units and then moving three units to the right.

Therefore, the translation is “two units down and three units to the right.”

Note that it doesn’t matter whether the horizontal or vertical translation happens first. We would still map AB onto CD if we first shifted three units to the right and then two units to the left.

Using mapping notation, this translation is $(x, y) → (x-3, y-2)$.

Example 2

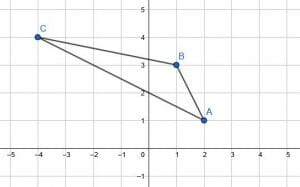
Translate the triangle horizontally two units to the left.

Example 2 Solution

To translate the triangle, first find the key points. In this case, those are the vertices. The coordinates of A are (2, 1), the coordinates of B are (1, 3), and the coordinates of C are (-4, 4).

Then, shift each vertex two units to the left by subtracting two from the x-value of its coordinates. When we do this, A becomes (0, 1), B becomes (-1, 3), and C becomes (-6, 4).

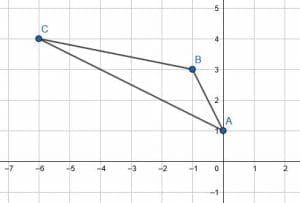
Now, connect these vertices as before to get the translated triangle.

Example 3

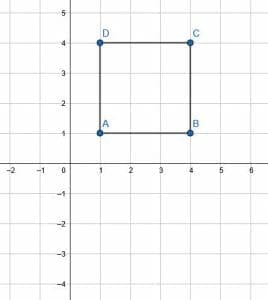
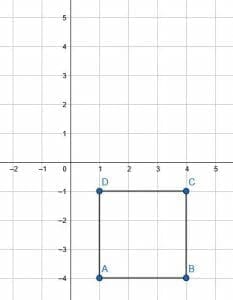
Translate the given square vertically 5 units downward.

Example 3 Solution

As before, use the vertices of the square as the key points. We notice that A is at (1, 1), B is at (4, 1), C is at (4, 4), and D is at (1, 4). Since this is a movement downward, we will subtract 5 from the y-value of each vertex. This will give the coordinates of the new figure.

When we do that, A becomes (1, -4), B becomes (4, -4), C becomes (4, -1), and D becomes (1, -1). Then, connect the point to complete the translated figure.

Example 4

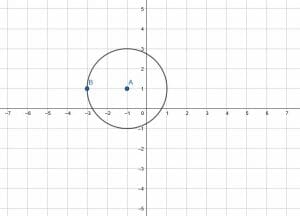
Translate the circle shown two units to the right and four units downward.

Example 4 Solution

First, decide on two key points. In this case, since A and B are given, it makes sense to use them. Typically, the center and one point on the circumference works for a circle.

Again, the order of translations doesn’t matter. For both A and B’s coordinates, add 2 to the x-value because the motion is to the right. Then, subtract 4 from the y-value because the motion is downward.

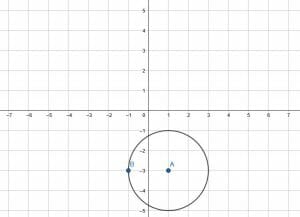
A becomes (1, -3) and B becomes (-1, -3). Using AB as a radius, construct the rest of the circle to complete the translation.

Example 5

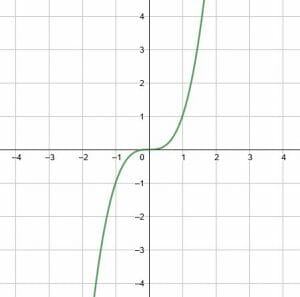
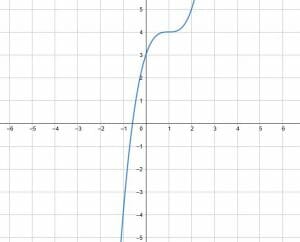
Translate the function shown right one unit and up four units.

Example 5 Solution

The function given is an $x^3$ function. In fact, the function is $y=x^3$. To translate this function, we can translate the vertex (0, 0) one unit right and four units up.

The new vertex is (1, 4). Then, we can sketch $x^3$ normally. All of the points will have a corresponding point that is one unit to the right and four units up.

Note that this function’s domain and range have not changed, but that is not always the case.

Also note that the function notation for this translation is $f(x)→f(x-1)+4$. This makes sense because the equation for the translated function is $y=(x-1)^3+4$.