Unit Circle Memorization – Explanation and Examples

Unit circle memorization involves memorizing the names of common angles and their corresponding sine and cosine ratios.Though memorizing the unit circle takes some up-front work, it makes trigonometry a million times easier. Otherwise, learners have to pull out a unit circle and look for values every single time they do a trigonometry problem, which can be incredibly tedious.Unit circle memorization is necessary for mastering trigonometry. Before continuing with the information in this section, make sure to review radian angles and the unit circle.

How To Memorize the Unit Circle

You can easily memorize the unit circle using the mnemonic ASAP, which is a trick to help with remembering something. In the case of the unit circle, the main things to memorize are the common angle measures in radians and where they fall on the circle and the sine and cosine values of these angles.Memorizing the unit circle is a lot like memorizing anything else. It requires a little bit of patience and dedication, and the process is easier with mnemonics. The easy way to remember the locations of angles on the circle is with the mnemonic ASAP. In this case, ASAP stands for “All, subtract, add, prime.”The easy way to remember the sine and cosine values of the angles is with the left hand trick.

Easy Way To Remember Unit Circle: ASAP

ASAP stands for “all, subtract, add, prime.” It is a mnemonic device used to remember the measure of the most important angles in a unit circle.Typically, an unlabelled unit circle looks like this.On such a circle, each of the radii represents an important angle. The acronym ASAP helps people remember them.

All

The first A, all, means that memorizing all of the angles in the first quadrants is necessary. The first is $2\pi$ (or $0$), then $\frac{\pi}{6}$, $\frac{\pi}{4}$,  and $\frac{\pi}{3}$. All of these angles have $\pi$ in the numerator and the denominators. Additionally, the largest denominator is closest to the x-axis, with values decreasing towards the y-axis.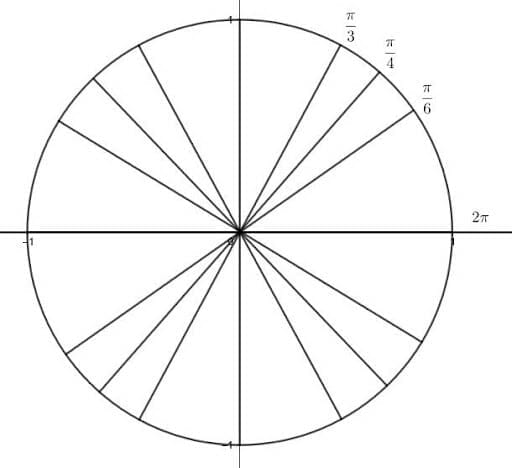

Subtract

The next quadrant has an S for “subtract.” This is because each angle, beginning with $\frac{\pi}{2}$ has a numerator coefficient of pi that is one less than the denominator. These denominators are the same ones as before ($3, 4$, and $6$), but in the opposite order.The next angle is $\pi$. Then, there is the third quadrant.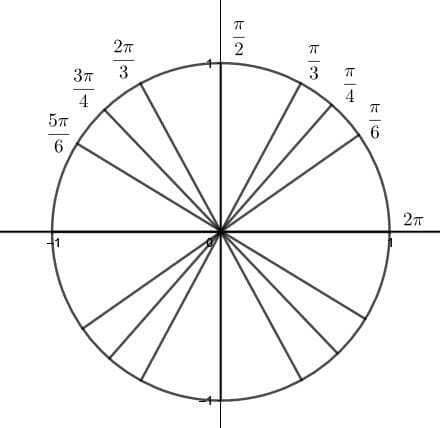

Add

After that, the third quadrant has the initial A for add. Each numerator coefficient of pi is one greater than the denominator. This means the angle closest to the x-axis is $\frac{7\pi}{6}$, the next is $\frac{5\pi}{4}$, the next is $\frac{4\pi}{3}$, and finally $\frac{3\pi}{2}$.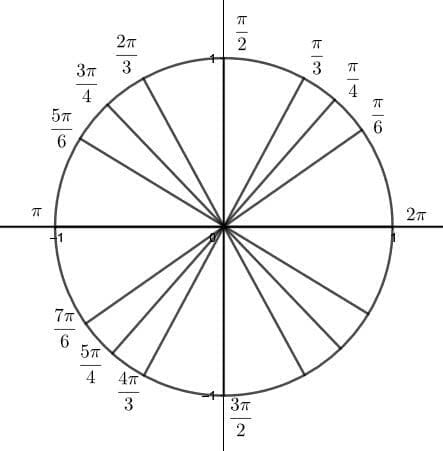

Prime

The last mnemonic, P for prime, actually also begins $\frac{3\pi}{2} radians. Each denominator in this quadrant follows the same progression, but the numerator coefficients for each are the primes, beginning with three, in increasing order. Thus, the angles are then $\frac{5\pi}{6}$, $\frac{7\pi}{4}$, and $\frac{11\pi}{3}$.When filling in the unit circle from memory, begin by writing $\frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}$ in each quadrant moving from the x-axis to the y-axis. Then fill in $2\pi$ and $\pi$ on the angles coterminal with the x-axis. Next, put $\frac{\pi}{2}$ on the two angles coterminal with the y-axis. Finally, fill in the numerator coefficients of pi in the second, third, and fourth quadrants using the mnemonic.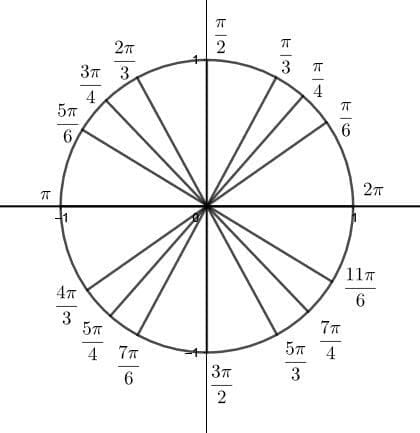

Left Hand Trick for Memorizing Sine and Cosine

Recall that the sine and cosine of an angle are equivalent to the intersection of the terminal ray and the unit circle’s circumference. For the common angles $\frac{\pi}{6}, \frac{\pi}{4},$ and $\frac{\pi}{3}$, these all have a denominator of two and a square root on top.Remembering these values for the first quadrant is simple with the left-hand trick. Then remembering where sine and cosine are positive and negative helps with the rest.To use the left hand trick, hold your left hand so that the palm is towards you, your thumb is straight up, and your pinky points straight to the right. Keep your other fingers relaxed.Your pinky represents the angle $2\pi$ or $0$, your ring finger is the angle $\frac{\pi}{6}$, the middle finger is the angle $\frac{\pi}{4}. Similarly, the index finger is $\frac{\pi}{3}, and the thumb is $\frac{\pi}{2}$ radians.That is, the pinky is the x-axis and the thumb is the y-axis.

Finding Sine and Cosine

Now to find the cosine and sine for the middle angles, bend the finger that corresponds to the angle. For example, to find the cosine of the angle $\frac{\pi}{6}$, bend the ring finger.The cosine relates to the number of fingers above the bent finger and the sine relates to the number of fingers below. There are three fingers above the bent finger and one below.Then, put these numbers in the square root in the numerator. Therefore, the cosine of $\frac{\pi}{6}$ is $\frac{\sqrt{3}}{2}$, and the sine is $\frac{\sqrt{1}}{2} = \frac{1}{2}$.Similarly, since there are two fingers above and below for $\frac{\pi}{4}$, the cosine and sine are both $\frac{\sqrt{2}}{2}$. Then, since there is one finger above the index finger, the cosine of $\frac{\pi}{3}$ is $\frac{\sqrt{1}}{2} = \frac{1}{2}$. Its sine, since there are three fingers below, is $\frac{\sqrt{3}}{2}$.

Other Quadrants

The final mnemonic to help with unit circle memorization is All Students Take Calculus. Taking the first letters of these words spells out ASTC. These mean “All, Sine, Tangent, Cosine,” which are the positive trig ratios in the first, second, third, and fourth quadrants, respectively. Since tangent is positive in the third quadrant and tangent is equal to sine divided by cosine, both sine and cosine are negative here.All of the major radii that have angles with a denominator of $6$ will have a cosine with an absolute value of $\frac{\sqrt{3}}{2}$ and a sine with an absolute value of $\frac{1}{2}$. Similarly, the absolute value of cosine and sine for major angles with a denominator of $4$ is $\frac{\sqrt{2}}{2}$. Finally, the absolute value of cosine and sine for major angles with a denominator of $3$ are $\frac{1}{2}$ and $\frac{\sqrt{3}}{2}$.For example, since cosine is negative in the second quadrant and sine is positive, the cosine and sine of $\frac{\pi}{4}$ are $-\frac{\sqrt{2}}{2}$ and $\frac{\sqrt{2}}{2}$, respectively.

Examples

This section goes over common examples of problems involving unit circle memorization and their step-by-step solutions.

Example 1

What are the sine and cosine values for the angle $\frac{5\pi}{4)$ radians?

Solution

The sine and cosine values for the angle $\frac{5\pi}{4}$ radians will have the same absolute value as the sine and cosine of the angle $\frac{\pi}{4}$ radians in the first quadrant. This is because the two angles are both major angles and have the same denominator.Take note that the numerator coefficient of pi, $5$, is one more than the denominator $4$ in the given angle. The mnemonic ASAP has “add” as the third letter, so the angle $\frac{5\pi}{4}$ radians must be in the third quadrant.Then, the mnemonic All Students Take Calculus has T as the third letter. This T stands for tangent, which is positive in the third quadrant. In this quadrant, then, neither sine nor cosine are positive. (If they were, this quadrant would also have an A for all).Therefore, the sine and cosine of $\frac{5\pi}{4}$ radians will both be negative.Finally, use the left hand trick to find the sine and cosine of $\frac{\pi}{4}$. The middle finger corresponds to this angle, and when that is bent there are two fingers above and below. Therefore, the cosine and sine are both $\frac{\sqrt{2}}{2}}$.This means that the cosine and sine of $\frac{5\pi}{2}$ are both $-\frac{\sqrt{2}}{2}$.

Example 2

What are the standard angles coterminal with $-\frac{\pi}{6}$, $-\frac{\pi}{4}$, and $-\frac{\pi}{3}$?

Solution

It helps to look at where these angles are on the unit circle.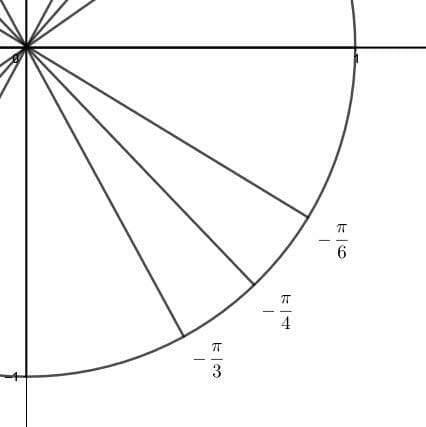These angles are the three major angles in the fourth quadrant.Then, in the mnemonic ASAP, P stands for prime. Therefore, all of the angles in this quadrant have prime numerator coefficients of pi, starting with the angle $\frac{3\pi}{2}$. The next angles moving towards the x-axis are $\frac{5\pi}{3}$, $\frac{7\pi}{4}$, and $\frac{11\pi}{6}$.These angles correspond to the angles $-\frac{\pi}{3}$, $-\frac{\pi}{4}$, and $-\frac{\pi}{6}$, respectively.

Example 3

Use the mnemonic All Students Take Calculus to determine where cotangent is positive and where it is negative.

Solution

The mnemonic All Students Take Calculus refers to the quadrants where the three main trigonometric functions are positive. Since cotangent is the reciprocal of tangent, it will have the same sign as tangent.In the first quadrant, all three of the main functions are positive. Therefore, cotangent will also be positive.In the second quadrant, sine is positive as the mnemonic indicates with the S for students. However, cosine is negative, so tangent and cotangent will be negative.Similarly, in the fourth quadrant, cosine is positive as the mnemonic indicates with the C for calculus. But, the sine is negative, making tangent and cotangent negative as well.The third quadrant, however, has a T for tangent. That is, tangent is positive in this quadrant, because sine and cosine are both negative. Therefore, cotangent is likewise positive.Thus, in the first and third quadrant, cotangent is positive.

Example 4

Find the coordinates of the points shown.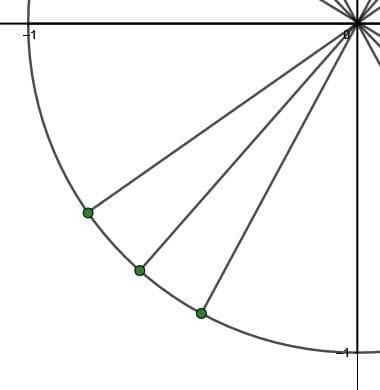

Solution

These points are the intersections of three radii and the unit circle. In particular, they are radii that form the three major angles in the third quadrant.These points will, by definition, be the sine and cosine of these angles.First, find the angles formed by the radii using the mnemonic ASAP. Since it is the third quadrant, the angles correspond to the second A for add. Therefore, working from the x-axis towards the y-axis, the angles are $\frac{7\pi}{6}$, $\frac{5\pi}{4}$ and $\frac{4\pi}{3}$.The coordinates of the corresponding points in the first quadrant are (using the left-hand trick), $(\frac{\sqrt{3}}{2}, \frac{1}{2})$, $(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})$, and $(\frac{1}{2}, \frac{\sqrt{3}}{2})$, respectively.In the third quadrant, however, only tangent is positive, as indicated by the mnemonic All Students Take Calculus. This means that both sine and cosine are negative.Therefore, the coordinates of the points are, working counterclockwise around the circle, $(-\frac{\sqrt{3}}{2}, -\frac{1}{2})$, $(-\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2})$, and $(-\frac{1}{2}, \-frac{\sqrt{3}}{2})$.

Example 5

Use the unit circle to find the values of secant and cosecant for the major angles in the second quadrant.

Solution

As in the above example, it helps to recall the values of sine and cosine for the angles in the first quadrant.Again, for the major angles, these are (working counterclockwise from the x-axis): $(\frac{\sqrt{3}}{2}, \frac{1}{2})$, $(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})$, and $(\frac{1}{2}, \frac{\sqrt{3}}{2})$. Here, the first coordinate is the cosine and the second is the sine.In the second quadrant, however, the mnemonic All Students Take Calculus indicates that only sine is positive. Therefore, all the cosines are negative. Thus, the cosine and sine ratios are, moving from the x-axis to the y-axis clockwise:

• $-\frac{\sqrt{3}}{2}$ and $\frac{1}{2}$ for $\frac{5\pi}{6}$,
• $-\frac{\sqrt{2}}{2}$ and $\frac{\sqrt{2}}{2})$ for $\frac{3\pi}{4},
• and $-\frac{1}{2}$ and $\frac{\sqrt{3}}{2})$ for $\frac{2\pi}{3}.

Now take the reciprocals to find the secant and cosecant, respectively.

• $-\frac{2}{\sqrt{3}}$ and $2$ for $\frac{5\pi}{6}$,
• $-\frac{2\sqrt{2}}{2}$ and $\frac{2\sqrt{2}}{2})$ for $\frac{3\pi}{4},
• and $-2$ and $\frac{2}{\sqrt{3}})$ for $\frac{2\pi}{3}.