Washer Method – Definition, Formula, and Volume of Solids

Learning about the washer method gives us the ability to calculate the volume of different types of solid formed from two functions. We’ve learned how to calculate solids of revolution given one function before. In this article, we’ll explore how our method changes as we add one more function.

The washer is an extension of the disk method.

This time, we’re calculating the volume of solids formed by rotating the region between two curves or functions.

Since the washer method uses a similar process as the disk method, it’s important that you have understood the math behind the disk method. We’ll also be using our techniques in calculating the area between two curves, so make you remember the key concepts for this topic. Do you think you’re ready? Then let’s dive right in and understand what makes this method unique!

What is the washer method?

The washer method allows us to calculate the volume of solids of revolution using cylindrical disks with holes. 

As we have mentioned, the washer method is an extension of the disk method. This technique is established so that we can also calculate for the volume of the solid returned by rotating the region bounded by two curves over the $\boldsymbol{x}$ or ${\boldsymbol{y}}$-axis.

Take a look at this image below – the disk was formed by rotating the rectangle on the left looks like an actual washer (it’s the flat ring we see in pipes of screws to ensure tightness). Hence, the name of this technique: the washer method.

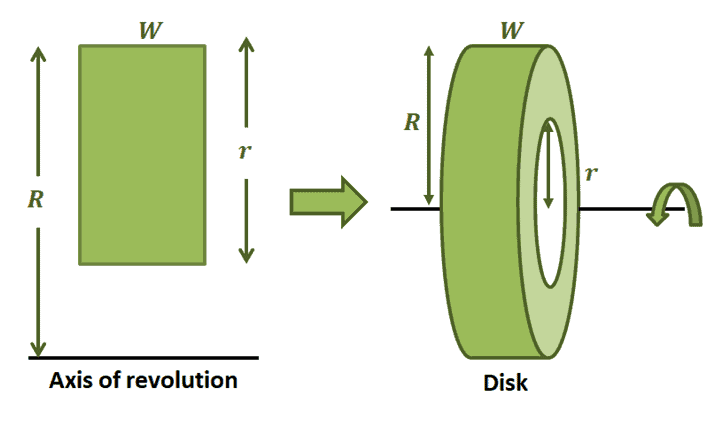
Why do we have a gap between the axis of revolution as well as the rectangular cross-section? That’s because we’re looking at the region formed between two curves. We’ve learned in the past that we can simply subtract the areas under the functions’ curves to find the area between the two. The result is represented by the rectangular section with $R$ representing the higher function and $r$ representing the lower function. This is why solids formed by the region between two functions have a gaping hole in the middle. Let’s first set an initial formula for the disk’s volume by subtracting the volume of the hole from the volume of the larger disk. Hence, we have:

\begin{aligned}V &= V_{\text{outer}} – V_{\text{inner}}\\&= (\pi R^2 W) – (\pi r^2 W) \\&= \pi W (R^2 – r^2)\end{aligned}

We can use this expression to establish the mathematical definition of the washer method.

Washer method definition

Let’s say we have two non-negative and continuous functions, $f(x)$ and $g(x)$, and $f(x)$ is always greater than or equal to $g(x)$ throughout the interval, $[a, b]$.We can define $R$ to be the region found between the two curves from $x = a$ to $x =b$.

The washer method allows us to calculate the volume of the solid formed by rotating $\boldsymbol{R}$ along the $x$-axis. In fact, the volume, $V$ can be expressed as shown below.

\begin{aligned}V&= \lim_{\Delta x \rightarrow 0} \sum_{i =0}^{n -1} \pi\{[f(x)]^2 – [g(x) ]^2\} \Delta x\\ &= \pi \int_{a}^{b} [f(x)]^2 – [g(x)]^2 \phantom{x} dx\end{aligned}

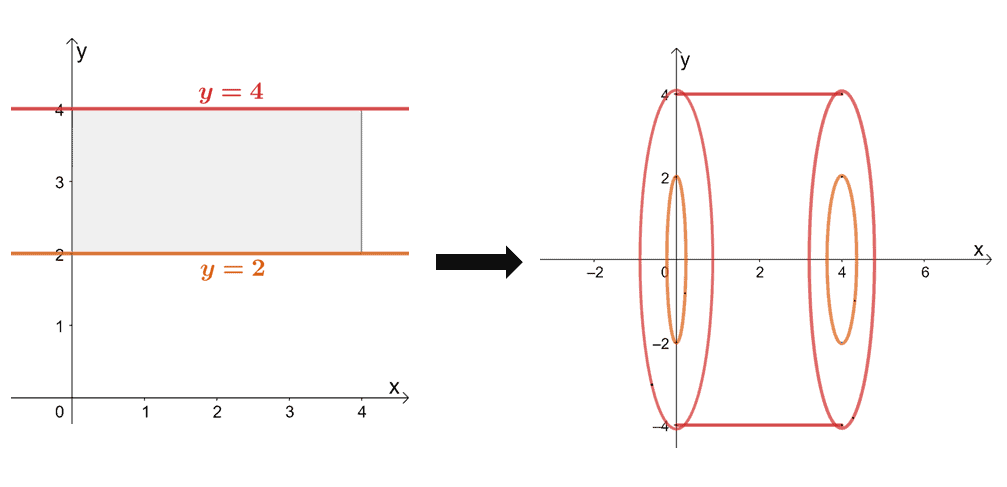
This means that the solid formed by rotating the region between curves is simply equal to the difference between their respective disks’ volumes. This also confirms what we know about the washer method – it is indeed an extension of the disk method.

Washer method formula

As with the disk method, we can also revolve the region between two curves about the $y$-axis. This means that we can also calculate the volume of the solid returned by this revolution.

Here are two graphs with each having a region enclosed by two curves. The left graph is to be revolved around the $x$-axis while the right graph is to be revolved with respect to the $y$-axis.

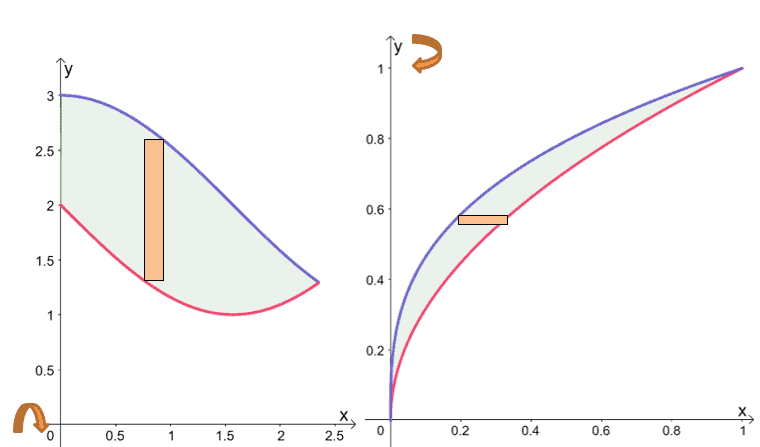
The variables in the formula for the volume will change depending on the axis of rotation. These are the two formulas defining the volume of the solid – one with respect to the $x$-axis and the other is about the $y$-axis.

Use the appropriate formula based on the direction we want to revolve the region. Keep in mind that the lower and upper limits for the horizontal revolution will be based on the horizontal bounds ($x =a$ and $x =b$). As for the vertical revolution, we’re basing the limits from $y =a$ to $y =b$.

How to use the washer method?

Once we understand how the washer method words, calculating the volume of the solid formed will then be straightforward. Here’s a quick guide to help you in setting up the graph and calculating the solid’s volume.

• Sketch the two functions’ curves to determine which of two lies above the other.
• Double-check if the curves meet the conditions of the washer method.
• When the bounds are not given, calculate for the functions’ points of intersection.
• Take note of the axis of revolution then apply the appropriate formula.
• Apply the appropriate definite integral properties and antiderivative

We’ve prepared some examples for you to work on and process the steps for the washer method. When you’re ready to work on more problems, head over to the next section as well.

Example 1

Determine the volume of the solid formed by rotating the region bounded by $y = (x- 3)^2$ and $y = x + 9$ about the $x$-axis.

Solution

Equate the two functions to find the points of intersection shared by the two functions.

\begin{aligned}(x – 3)^2 &= x + 9\\ x^2 – 6x + 9&= x + 9\\x^2 – 7x &= 0\\ x(x -7) &= 0\\x&= 0, 7\\\\\boldsymbol{(x, y)} &\boldsymbol{= (0,0) , (7, 16)}\end{aligned}

Graph the two functions and use their points of intersection as a guide.

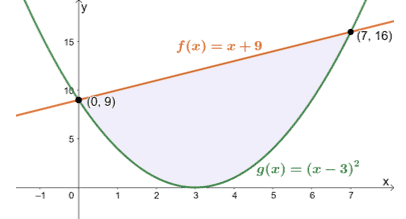
Since $y = x+ 9$ lies above the parabola, $y = (x -3)^2$, we can subtract $g(x) = (x -3)^2 = x^2 – 6x + 9$ from $f(x) = x + 9$. Use the formula for the solid rotated about the horizontal axis, $V = \pi \int_{a}^{b} [f(x)]^2 – [g(x)]^2 \phantom{x} dx $.

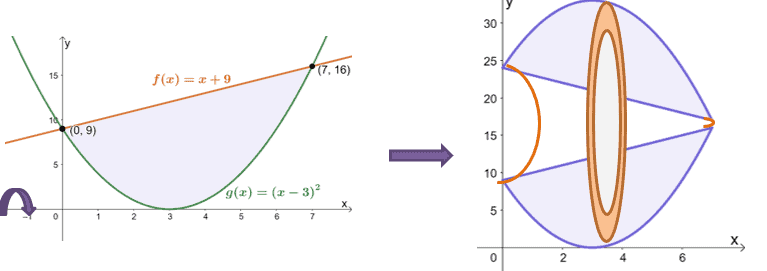
Let’s begin by simplifying $[f(x)]^2 – [g(x)]^2$ then integrate the resulting expression to calculate the solid’s volume. Use the bounds, $x =0$ and $x =7$, as the lower and upper limits of the definite integral.

\begin{aligned}V&= \pi \int_{0}^{7} [(x +9)^2 -[(x – 3)^2]^2] \phantom{x}dx\\&= \pi \int_{0}^{7}[(x + 9)^2 – (x -3)^2]\phantom{x}dx\\&= \pi \int_{0}^{7}(-x^4 + 12x^3- 53x^2 + 126x) \phantom{x}dx\\&= \pi \left[-\dfrac{x^{4+ 1}}{4 +1} + \dfrac{12x^{3 +1}}{3 + 1} -\dfrac{53x^{2 +1}}{2 + 1} + \dfrac{126x^{1 +1}}{1 + 1}\right ]_{0}^{7}\\&= \pi \left[-\dfrac{x^5}{5} + 3x^4 -\dfrac{53x^3}{3} + 63x^2\right]_{0}^{7}\\&= \dfrac{13034\pi }{15} \\& \approx2729.83\end{aligned}

This means that the solid formed by rotating the region between the curves, $y =x+9$ and $y = (x -3)^2$, has a volume of $\dfrac{13034\pi}{15}$ or approximately $2729.83$.

Example 2

Calculate the volume of the solid formed by rotating the region bounded by $y = \sqrt{x}$ and $x = 4$ about the $y$-axis.

Solution

Since we’re rotating the graph about the $y-axis$, let’s rewrite the first equation as a function of $y$.

\begin{aligned} (y)^2 &= (\sqrt{x})^2 \\y^2 &= x\\x &= y^2\end{aligned}

Graph the two curves and we’ll see that $f(y) = 4$ lies at the rightmost position than $g(y) = x^2$. We’re only dealing with the region above the $x$-axis since the washer method can only applied on non-negative and continuous functions.

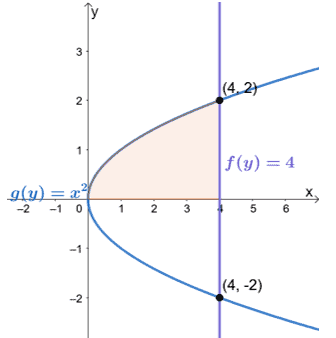
This means that we’re rotating the region between $f(y) = 4$ and $g(y) =x^2$ from $y = 0$ to $y= 2$. Apply the formula for the solid rotated about the vertical axis, $V = \pi \int_{a}^{b} [f(y)]^2 – [g(y)]^2 \phantom{x} dy$. Use the vertical bounds for the definite integral’s lower and upper limits.

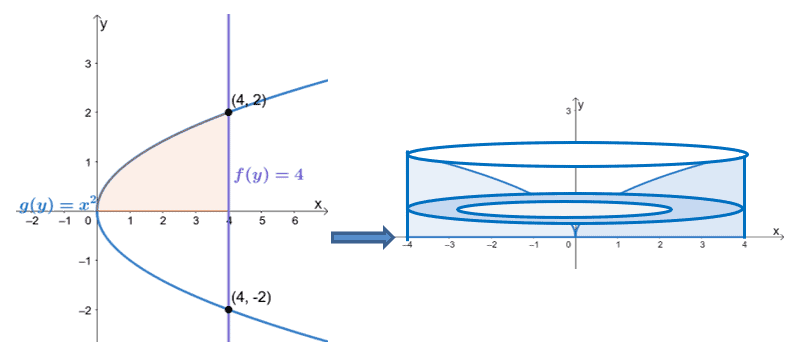
Here’s an illustration of how the region is rotated with respect to the $y$-axis. Hence, we can calculate the volume of the resulting solid as shown below.

\begin{aligned}V &= \pi \int_{a}^{b} [f(y)]^2 -[g(y)]^2 \phantom{x} dy\\ &= \pi \int_{0}^{2} [(4)^2 – (y^2)^2] \phantom{x}dy\\&= \pi \int_{0}^{2}(16 – y^4) \phantom{x}dy\\&= \pi\left[16y – \dfrac{y^{4 +1}}{4 +1} \right ]_{0}^{2}\\&= \pi \left[16y – \dfrac{y^5}{5} \right ]_{0}^{2}\\&= \dfrac{128\pi}{5}\\& \approx 80.425\end{aligned}

This means that the solid formed by revolving the region between the two curves about the $y$-axis will have a volume of $\dfrac{128\pi}{5}$ or approximately $80.425$.

Practice Questions

1. Determine the volume of the solid formed by rotating the region bounded by $y = (x- 4)^2$ and $y = x + 16$ about the $x$-axis.

2. Calculate the volume of the solid formed by rotating the region bounded by $y = x^2$ and $y = \sqrt{x}$ about the $x$-axis.

3. Determine the volume of the solid formed by rotating the region bounded by $y =4 -\sqrt{x}$ and $y = 4 – x^2$ about the $x$-axis.

4. Calculate the volume of the solid formed by rotating the region bounded by $x = y^3$ and $x = 4y$ about the $y$-axis.

5. Determine the volume of the solid formed by rotating the region bounded by $y = 2 + \sqrt{1 -y^2}$ and $x = 2 – \sqrt{1 – y^2}$ about the $y$-axis.

Answer Key

1. The solid has a volume of $\dfrac{15066\pi}{5} $ or approximately $9466.247$.
2. The solid has a volume of $\dfrac{3\pi}{10} $ or approximately $0.942$.
3. The solid has a volume of $\dfrac{71\pi}{30} $ or approximately $7.435$.
4. The solid has a volume of $\dfrac{512\pi}{21} $ or approximately $76.595$.
5. The solid has a volume of $4\pi^2 $ or approximately $39.478$.

Images/mathematical drawings are created with GeoGebra.