JUMP TO TOPIC
Zero Angle – Explanation and Examples
A zero angle is an angle with a measure of zero degrees or zero radians.
An angle with a measure of zero degrees differs from an angle with a measure of 180 degrees based on the location of the endpoints and vertex of the angle.
Zero angles are important in geometry and trigonometry.
Before moving forward with this section, make sure to review angles and types of angles.
This article covers:
- What is Zero Angle?
- Zero Angle Definition
- Zero Angle Example
What is Zero Angle?
A zero angle is an angle with a measure of zero degrees or zero radians.
Recall that an angle is two rays meeting at a common endpoint called the vertex. Angles are then named by a point on one ray, the vertex, and a point on the second ray.
Measuring an angle counterclockwise makes the angle positive. Measuring it clockwise, however, makes it negative when orientation and rotation are important (such as in trigonometry).
Consequently, then, it is also possible to have a zero angle. To picture this, imagine collapsing an angle on itself until the two rays meet.
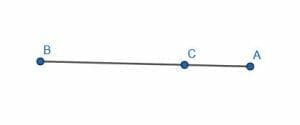
That is, a zero angle consists of three points on a ray. An angle $ABC$ with vertex $B$ has an endpoint $B$ and the points $A$ and $C$ on the same side of the endpoint on the ray.
Zero Angles and Trigonometry
Zero angles play an important role in trigonometry.
Recall that trigonometric functions have angles as their inputs and ratios as their outputs. They also have periodic graphs.
These zero angles are the y-intercepts of these trigonometric graphs.
Additionally, since most trigonometric graphs are $2\pi$ periodic, meaning they repeat every $2\pi$ radians, the trigonometric function’s value at $0$ is equal to its value at $n\pi$, where $n$ is an even number.
Constructing a Zero Angle
To construct a zero angle, construct two points.

Then, draw a line connecting these two points using a straightedge.

Finally, draw a third point on the line.

Then, the angle $ABC$ and the angle $CBA$ are both zero angles. Alternatively, the angles $BAC$ and $CAB$ are also zero angles.
Note that this is different from the angle $BCA$ or $ACB$, which are $180$ degree angles. The vertex in this case is in the middle, so the angle measures above or below the line instead of along the line.
Zero Angle Definition
A zero angle is an angle with a measure of zero units. Typically, these units are degrees or radians.
Functionally, a zero angle is an angle that lies on a line where the vertex lies on the line to the left or right of both other points on the angle.
Sometimes the zero angle is also called the null angle.
Zero Angle Example
In trigonometric graphs, the zero angle is the y-intercept of the graph.
For example, consider the function $sinx$.
Recall that $sinx$ is a function that takes an angle in a right triangle and finds the ratio of the opposite side length over the hypotenuse side length.
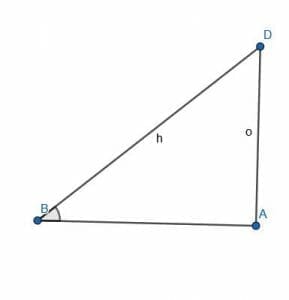
In the above figure, the sine of the angle $ABD$ is $\frac{o}{h}$.
Consider, however, what happens as the angle $ABD$ goes to $0$.
As the angle gets smaller, the length of $o$ decreases and the length of $h$ increases. This means that $\frac{o}{h}$ will also decrease.
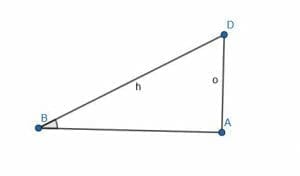
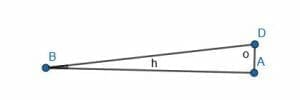
When the length of $o$ becomes $0$, the angle $ABD$ also becomes $0$. This means that when the point $D$ coincides with $A$, $o$ is equal to $0$, $DBA$ is $0$, and the ratio $\frac{o}{h} = sinx$ is also $0$.
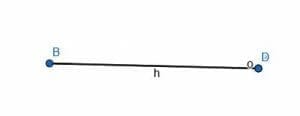
Although most people would not consider this a triangle, what happens at this point is still important in terms of limits. That is, it is important to consider what happens as the length of $o$ gets infinitely close to $0$.
Common Examples
This section covers common examples of problems involving zero angles and their step-by-step solutions.
Example 1
Find the measure of the following angles:

$CDA$
$DAB$
$BAD$
$ADC$
$DBC$
Solution
$DAB, BAD,$ and $DBC$ are zero angles. The angles $CDA$ and $ADC$ are $180$ degree angles.
Clearly, all of these angles lie along a straight line. Why are some of them zero angles and some of them $180$ degree angles?
The basic difference is that the order of the points in the $180$ degree angles lie in a straight line from left to right or right to left. The zero angles change direction.
Take, for example, the angle $DAB$. The line segment $DA$ goes from the upper right to the lower left. The line segment $AB$, however, goes from the lower left to the upper right.
This contrasts with the angle $CDA$. The line segment $CD$ extends from the upper right to the lower left. Then, the line $DA$ does the same. This, therefore, is a $180$ degree angle, not a zero angle.
Example 2
The sine function is odd. This means that for every angle $\theta$, $sin(-\theta) = -sin(\theta)$.
Find an angle for which $sin(-\theta) = sin(\theta)$.
Solution
Since the sine function is odd, an angle for which $sin(-\theta) = sin(\theta)$ is an angle for which $-sin(\theta) = sin(\theta)$ because $-sin(\theta) = sin(\theta)$.
But, if $-sin(\theta) = sin(\theta)$, then the sine of this angle must be equal to zero. This is because $sin(\theta)$ will be a number(a ratio), and the only number that is equal to its own negative is zero.
Therefore, $\theta$ is an angle for which the ratio of the opposite side divided by the hypotenuse is $0$. Therefore, the length of the opposite side must be zero.
If the length of the opposite side is zero, however, the angle itself must be equal to $0$. Such a figure would be a straight line, not a true triangle.
Therefore, $\theta$ is equal to zero or (since sine is $2\pi$ periodic) some whole number multiple of $2\pi$.
Example 3
Construct a zero angle.
Solution
A zero angle is one of the easiest angles to construct. Since the zero angle lies on a straight line, begin by constructing a straight line.
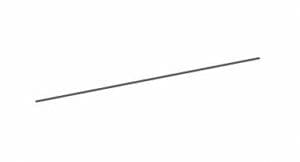
Next, add three distinct points to the line. Call these points $A$, $B$, and $C$.
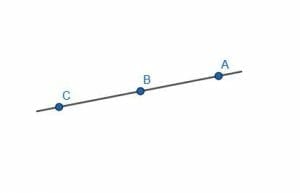
There are two angles now with a measure of zero degrees. These are angle $ACB$ or $BCA$ and angle $CAB$ or $BAC$.
Note that the angle $CBA$ or $ABC$ is a $180$ degree angle.
Example 4
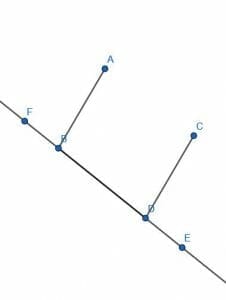
Line $AB$ is parallel to the line $CD$. The line $EF$ passes through both lines.
What is the difference between the measure of the angle $ABD$ and the measure of the angle $CDE$?
Solution
This problem requires a little bit of background knowledge about parallel lines.
A line cutting two parallel lines is called a transversal. In this case, the line $EF$ is a transversal cutting the parallel lines $AB$ and $CD$.
Additionally, when a transversal cuts through the parallel lines, it creates corresponding angles that are equal. Therefore, the angles $ABF$ and $CDB$ are equal as are the angles $ABD$ and $CDE$.
Therefore, the angle measures of the angles in question, $ABD$ and $CDE$, will be the same.
Thus, the difference will be $0$ degrees or the zero angle.
Example 5
A point $A$ lies on a circle with center $B$. Find the arc length of the segment that begins and ends at the point $A$.
Solution
The arc length of two points on a circle is the measure of the angle between two radii connecting the points to the center of the circle.
In this case, however, since the arc only has one point, the radii are just one radius connecting the point $A$ to the center $B$. Therefore, the arc length is the measure of the angle $ABA$, which is the zero angle. Thus, the arc length is $0$ degrees or $0$ radians.
More Examples with Explanation
- Cosine is the ratio of the adjacent line and the hypotenuse in a right triangle. As the angle goes to zero, what happens to the cosine?
- Using the above information and the information from example 2, what is the tangent of the zero angle? That is, what is the ratio of the opposite side to the adjacent side as the angle in a right triangle goes to zero?
- Construct a zero angle at the point $A$.
- A gymnast walks along a flat balance beam. What is the angle of incline for the gymnast’s walk?
- What is the difference between the measures of any two angles in a rectangle?
Answer Key
- The hypotenuse collapses onto the adjacent angle, so the ratio goes to $1$ as the angle goes to $0$.
- Tangent is also equal to the sine divided by the cosine. Therefore, for the zero angle, the tangent goes to $0$, like sine.
- $0$ degrees or $0$ radians because it is a flat surface.
- $0$ degrees or $0$ radians because all of the angles in a rectangle have the same measure.
